
Kartografiske fremskrivninger hvad de er for og typer

Det kartografiske fremskrivninger er repræsentationer på et plan af de punkter, der er på jordens overflade, som er buet. På denne måde konverteres en lokalitets koordinater: bredde og længdegrad, til et punkt med kartesiske koordinater x og y.
Det er selvfølgelig ikke let, da dette betyder "udfladning" af jordens kugle, hvilket ikke kan gøres uden deformation. Faktisk er dette, hvad der sker på de fleste kort.
Læseren kan prøve at fjerne skrælen midt i en appelsin og derefter prøve at gøre den helt flad. Den eneste måde at opnå dette på er ved at bryde det i nogle dele, men på denne måde er det klart, at overfladen deformeres ganske lidt..
Af denne grund falder hverken længderne, retningerne eller figurerne repræsenteret på kortene nøjagtigt sammen med de rigtige eller i det mindste ikke alle disse egenskaber på samme tid. Når en af dem bevares, går de andre på en eller anden måde tabt, i det mindste delvist. Afhængigt af formålet med kortet kan sådanne tab dog være acceptabelt..
På trods af dette har flade gengivelser af jordens overflade mange fordele. Til at begynde med er kort bærbare og kan tages mange steder uden at tage for meget plads.
Derudover kan de fremstilles specielt til bestemte regioner og forstørre de detaljer, der betragtes som vigtige, hvilket minimerer deformation. Dette er ikke muligt med en mere realistisk repræsentation, som nødvendigvis er mindre: en verden til målestok..
Globus er bygget efter jordens form, men af størrelsesårsager kan de ikke indeholde meget information.
Artikelindeks
- 1 Typer af kortfremspring
- 1.1 - I henhold til de bevarede egenskaber ved projektionen
- 1.2 - I henhold til figuren, som den projiceres på
- 2 Mest populære kartografiske fremskrivninger
- 2.1 Mercator-projektion
- 2.2 Lambert konisk projektion
- 3 Modificerede kortfremskrivninger
- 3.1 Sinusformet projektion
- 3.2 Mollweide-projektion
- 3.3 Goode-projektion
- 4 Referencer
Typer af kortfremspring
- I henhold til de bevarede egenskaber ved projektionen
Afhængig af de egenskaber, der bevares i fremskrivningen, er der følgende typer kartografiske fremskrivninger:
-Ifølge: opretholder de eksisterende vinkler mellem to linjer på jordoverfladen, derfor er det en passende projektion til navigationskort
-Tilsvarende (lige areal): Denne fremspring holder terrænoverfladerne korrekte, selvom der kan forekomme deformation, og formene ikke længere er ens. Det er den passende fremskrivning til pakkekort.
-Lige langt fra hinanden: som navnet antyder, holdes afstanden mellem to punkter i denne projektion identisk, forbundet med en bue på jordoverfladen og med en lige linje på kortet.
-Fylaktisk- Vinkler, overflader og afstande bevares ikke i denne fremspring, men formforvrængning er minimal.
- Ifølge figuren, hvor den projiceres
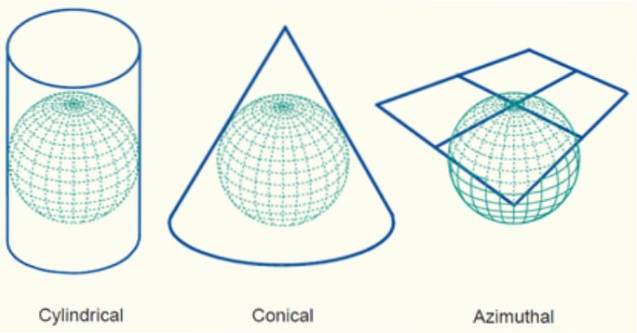
Der er mange, mange måder at lave fremskrivninger på. Et andet meget anvendt kriterium er at klassificere efter planfiguren, som den projiceres på, som f.eks. Kan være et plan, en cylinder eller en kegle..
Når du bruger et plan, kaldes projektionen plan eller azimutfremspring, hvorimod når en geometrisk figur bruges, så er den en vækst, fordi den geometriske figur kan udvikle sig senere til at blive et plan, som vi vil se nedenfor.
Plan- eller azimutale fremspring
De er bygget fra projektionen af jordoverfladen fra et punkt kendt som projektionshoved, mod et plan, der tangerer jordens overflade. Punktet for tangens kaldes projektionscenter.
Denne type projektion har flere varianter, afhængigt af placeringen af både projektionshovedet og planet for tangens..
Konisk fremspring
Keglen og cylinderen er de geometriske figurer, der mest bruges som hjælpemidler til at udvikle fremspringet. I det første tilfælde er konisk fremspring, kuglen er dækket af en kegle, hvis symmetriakse passerer gennem polerne.
Nu, på jordens overflade, trækkes buede linjer for at placere hvert punkt: parallellerne og meridianerne. Når man projicerer på keglen, vises parallellerne som koncentriske cirkler, mens meridianerne vises som samtidige linjer i keglens toppunkt.
Cylindrisk fremspring
I cylindrisk fremspring, jordens overflade er dækket af en cylinder, der tangerer til kuglen, hvor cylinderens akse er parallel med aksen, der passerer gennem polerne. Derefter forlænges cylinderen, hvorpå meridianerne og parallellerne forbliver som lige linjer.
Linjerne, der svarer til meridianerne, vil være lige store, men ikke dem, der svarer til parallellerne, hvis afstand øges, når længdegraden øges..
Imidlertid kan cylinderen placeres på en anden måde og ikke nødvendigvis berøre jordoverfladen på ækvator, som vist på figuren. Cylinderen kan have en diameter, der er mindre end Jordens.
Mest populære kortfremskrivninger
De ovenfor beskrevne typer fremskrivninger kan kombineres for at danne nye fremskrivninger. De mest kendte er kort beskrevet nedenfor..
Mercator-projektion
Det er blandt de mest anvendte fremskrivninger til at repræsentere verdenskort. Det blev opfundet af geografen Gerard Kremer, også kendt som Gerardus Mercator (1512-1594) i år 1569.
Det er en tilpasset cylindrisk fremspring, det vil sige, den respekterer vinklerne, hvorfor det er en fremspring, der er meget værdsat af søfolk. Det bevarer imidlertid ikke områder, da denne type projektion er passende for ækvatoriale områder. Uden for disse breddegrader ser regioner meget større ud, end de virkelig er.
På trods af disse ulemper er det fremskrivningen, der bruges i de mest populære kortapplikationer på internettet..
Lambert konisk projektion
Denne projektion blev skabt af den schweiziske matematiker Johann Lambert (1728-1777), som også viste, at tallet π er irrationelt. Denne fremspring bevarer afstande meget godt og er meget velegnet til at repræsentere mellembreddegrupper, men den er ikke egnet til ækvatoriale breddegrader på grund af deformation..
Modificerede kortfremspring
Denne gruppe fremspring bruges til at repræsentere jordens overflade og forsøger at minimere deformationer. Blandt de bedst kendte er:
Sinusformet projektion
Denne fremspring tillader, at parallellerne er vandrette og lige langt fra hinanden, i modsætning til den cylindriske fremspring. Den centrale meridian er en linje vinkelret på parallellerne, men de andre meridianer kurver rundt.
Afstandene mellem parallellerne såvel som mellem parallellerne og den centrale meridian er sande, og det bevarer også områderne.
Mollweide projektion
Denne projektion søger at bevare områderne. Her er ækvator dobbelt så lang som den centrale meridian. Meridianerne har form af ellipser, og parallellerne er vandrette linjer parallelt med ækvator, hvis adskillelse afhænger af den trofaste bevarelse af områderne, hvilket er meget passende for mellemstore breddegrader..
Goode projektion
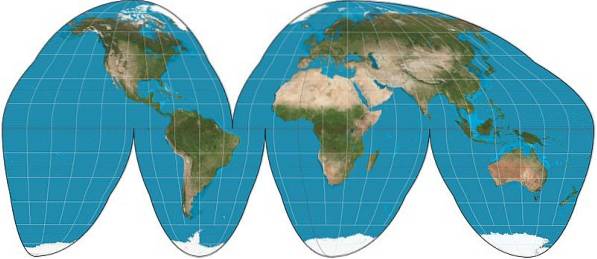
Dette er en projektion, der i modsætning til de foregående er diskontinuerlig. I den er jordens overflade repræsenteret i form af uregelmæssige og forenede områder, hvilket minimerer forvrængningen på kontinenterne. Ikke så i oceaniske overflader, som er opdelt, som det kan ses i figuren.
Goode-fremskrivningen har dog den fordel, at den bevarer kontinentenes og områdets form, hvorfor den i vid udstrækning anvendes i økonomiske kort til at repræsentere distributionen af produkter over hele verden..
Referencer
- Aguilar, A. 2004. Generel geografi. 2. plads Udgave. Pearson Uddannelse.
- Gisgeografi. Hvad er kortfremskrivninger? Gendannet fra: gisgeography.com
- Snaider, P. Kartografiske fremskrivninger og referencesystemer. Gendannet fra: hum.unne.edu.ar.
- USGS. Kortfremspring. Gendannet fra: icsm.gov.au
- Wikipedia. Liste over kortfremspring. Gendannet fra: en.wikipedia.com


Endnu ingen kommentarer