
Reduktion af lignende vilkår (med løste øvelser)

Det reduktion af lignende vilkår er en metode, der bruges til at forenkle algebraiske udtryk. I et algebraisk udtryk er lignende udtryk dem, der har den samme variabel; det vil sige, de har de samme ukendte repræsenteret af et bogstav, og disse har de samme eksponenter.
I nogle tilfælde er polynomerne omfattende, og for at nå frem til en løsning skal man forsøge at reducere udtrykket; Dette er muligt, når der er udtryk, der ligner hinanden, som kan kombineres ved at anvende operationer og algebraiske egenskaber såsom addition, subtraktion, multiplikation og division..

Artikelindeks
- 1 Forklaring
- 2 Sådan foretages en reduktion af lignende vilkår?
- 2.1 Eksempel
- 2.2 Reduktion af lignende udtryk med lige tegn
- 2.3 Reduktion af lignende udtryk med forskellige tegn
- 3 Reduktion af lignende vilkår i operationer
- 3.1 I summer
- 3.2 I subtraktion
- 3.3 I multiplikation
- 3.4 I divisioner
- 4 Løst øvelser
- 4.1 Første øvelse
- 4.2 Anden øvelse
- 5 Referencer
Forklaring
Lignende udtryk er dannet af de samme variabler med de samme eksponenter, og i nogle tilfælde er disse kun differentieret med deres numeriske koefficienter.
Lignende udtryk betragtes også som dem, der ikke har variabler; det vil sige de udtryk, der kun har konstanter. Så for eksempel er følgende som udtryk:
- 6xto - 3xto. Begge udtryk har den samme variabel xto.
- 4. pladstob3 + 2. pladstob3. Begge termer har de samme variabler atob3.
- 7 - 6. Udtrykkene er konstante.
De termer, der har de samme variabler, men med forskellige eksponenter, kaldes forskellige udtryk, såsom:
- 9atob + 5ab. Variabler har forskellige eksponenter.
- 5x + og. Variablerne er forskellige.
- b - 8. Det ene udtryk har en variabel, det andet er en konstant.
Ved at identificere de samme udtryk, der danner et polynom, kan disse reduceres til et ved at kombinere alle dem, der har de samme variabler med de samme eksponenter. På denne måde forenkles udtrykket ved at reducere antallet af udtryk, der komponerer det, og beregningen af dets løsning letter..
Sådan foretages en reduktion af lignende vilkår?
Reduktionen af lignende vilkår sker ved at anvende den associerende egenskab ved tilføjelse og produktets distribuerende ejendom. Ved hjælp af følgende procedure kan du foretage en begrebsreduktion:
- Lige vilkår grupperes først.
- Koefficienterne (de tal, der ledsager variablerne) for de samme termer tilføjes eller trækkes fra, og de associerende, kommutative eller distribuerende egenskaber anvendes, alt efter omstændighederne..
- Derefter skrives de opnåede nye vilkår og placerer det tegn, der er resultatet af operationen, foran dem.
Eksempel
Reducer udtryk for følgende udtryk: 10x + 3y + 4x + 5y.
Opløsning
For det første beordres vilkårene til at gruppere dem, der er ens, ved anvendelse af kommutativ ejendom:
10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.
Derefter anvendes den distribuerende egenskab, og koefficienterne, der ledsager variablerne, tilføjes for at opnå reduktion af vilkårene:
10x + 4x + 3y + 5y
= (10 + 4) x + (3 + 5) y
= 14x + 8 år.
For at reducere lignende vilkår er det vigtigt at tage højde for tegnene på koefficienterne, der ledsager variablen. Der er tre mulige tilfælde:
Reduktion af lignende udtryk med lige tegn
I dette tilfælde tilføjes koefficienterne, og vilkårstegnet placeres foran resultatet. Derfor, hvis de er positive, vil de resulterende vilkår være positive; i tilfælde af at vilkårene er negative, får resultatet tegnet (-) ledsaget af variablen. For eksempel:
a) 22abto + 12abto = 34 abto.
b) -18x3 - 9x3 - 6 = -27x3 - 6.
Reduktion af lignende udtryk cpå forskellige skilte
I dette tilfælde trækkes koefficienterne, og tegnet på den største koefficient placeres foran resultatet. For eksempel:
a) 15xtoy - 4xtoog + 6xtoy - 11xtoY
= (15xtoog + 6xtoy) + (- 4xtoy - 11xtoY)
= 21xtoy + (-15xtoY)
= 21xtoy - 15xtoY
= 6xtoY.
b) -5a3b + 3 a3b - 4a3b + a3b
= (3 til3b + a3b) + (-5a3b - 4a3b)
= 4a3b - 9a3b
= -5 til3b.
For at reducere lignende udtryk, der har forskellige tegn, dannes der et enkelt additivudtryk med alle dem, der har et positivt tegn (+), koefficienterne tilføjes, og resultatet ledsages af variablerne.
På samme måde dannes et subtraktivt udtryk med alle de termer, der har et negativt tegn (-), tilføjes koefficienterne, og resultatet ledsages af variablerne.
Endelig trækkes summen af de to dannede udtryk, og tegnet på det større placeres fra resultatet.
Reduktion af lignende vilkår i operationer
Reduktion af lignende udtryk er en operation af algebra, som kan anvendes i tillæg, subtraktion, multiplikation og algebraisk division.
I summer
Når du har flere polynomier med lignende udtryk, for at reducere dem bestilles vilkårene for hvert polynom, så de holder deres tegn, så skrives de efter hinanden, og lignende vilkår reduceres. For eksempel har vi følgende polynomer:
3x - 4xy + 7xtoog + 5xyto.
- 6xtoy - 2xy + 9 xyto - 8x.
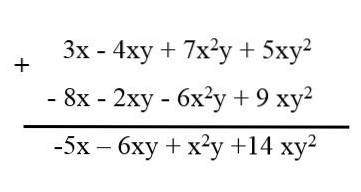
I subtraktion
For at trække et polynom fra et andet, skrives minuend, og derefter ændres subtraend med dets tegn, og derefter er reduktionen af de lignende termer udført. For eksempel:
5. plads3 - 3abto + 3btoc
6abto + 2. plads3 - 8btoc
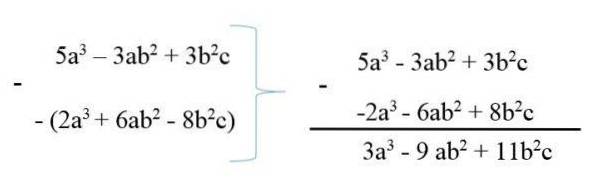
Polynomierne opsummeres således til 3a3 - 9abto + 11btoc.
I multiplikationer
I et produkt af polynomier multipliceres termerne, der udgør multiplikatoren, med hvert udtryk, der udgør multiplikatoren, i betragtning af at tegnene på multiplikationen forbliver de samme, hvis de er positive.
De ændres kun, når de ganges med et udtryk, der er negativt; når to termer af det samme tegn multipliceres, vil resultatet være positivt (+), og når de har forskellige tegn, vil resultatet være negativt (-).
For eksempel:
a) (a + b) * (a + b)
= ato + ab + ab + bto
= ato + 2ab + bto.
b) (a + b) * (a - b)
= ato - ab + ab - bto
= ato - bto.
c) (a - b) * (a - b)
= ato - ab - ab + bto
= ato - 2ab + bto.
I divisioner
Når du vil reducere to polynomer gennem en division, skal du finde et tredje polynom, der, når det ganges med det andet (divisor), resulterer i det første polynom (dividend).
For det skal vilkårene for udbyttet og divisoren bestilles fra venstre mod højre, så variablerne i begge er i samme rækkefølge.
Derefter uddeles, startende fra den første periode til venstre for udbyttet med den første periode til venstre for divisoren, idet der altid tages hensyn til tegnene på hver periode.
Reducer f.eks. Polynomet: 10x4 - 48x3og + 51xtoYto + 4xy3 - 15 år4 dividerer det med polynomet: -5xto + 4xy + 3yto.
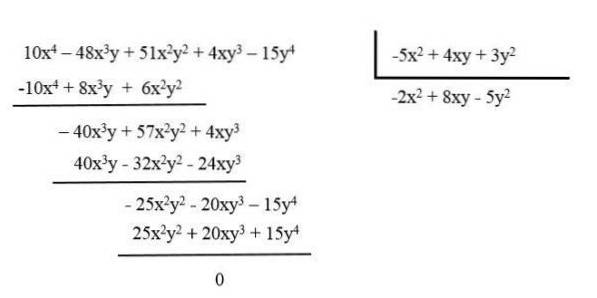
Det resulterende polynom er -2xto + 8xy - 5 årto.
Løst øvelser
Første øvelse
Reducer vilkårene for det givne algebraiske udtryk:
15.to - 8ab + 6ato - 6ab - 9 + 4ato - 13 ab.
Opløsning
Den kommutative egenskab ved tilføjelse anvendes og grupperer de termer, der har de samme variabler:
15.to - 8ab + 6ato - 6ab + 9 + 4ato - 13
= (15ato + 6.to + 4. pladsto) + (- 8ab - 6ab) + (9 - 13).
Derefter anvendes den fordelende egenskab af multiplikation:
15.to - 8ab + 6ato - 6ab + 9 + 4ato - 13
= (15 + 6 + 4) ato + (- 8 - 6) ab + (9 - 13).
Endelig forenkles de ved at tilføje og trække koefficienterne for hvert udtryk:
15.to - 8ab + 6ato - 6ab + 9 + 4ato - 13
= 25ato - 14ab - 4.
Anden øvelse
Forenkle produktet af følgende polynomer:
(8x3 + 7xyto)*(8x3 - 7 xyto).
Opløsning
Hvert udtryk i det første polynom multipliceres med det andet under hensyntagen til, at tegnene på termerne er forskellige; derfor vil resultatet af dets multiplikation være negativt, såvel som eksponentens love skal anvendes.
(8x3 + 7xyto) * (8x3 - 7xyto)
= 64 x6 - 56 x3* xyto + 56 x3* xyto - 49 xtoY4
= 64 x6 - 49 xtoY4.
Referencer
- Angel, A. R. (2007). Elementær algebra. Pearson Uddannelse,.
- Baldor, A. (1941). Algebra. Havana: Kultur.
- Jerome E. Kaufmann, K. L. (2011). Elementær og mellemliggende algebra: En kombineret tilgang. Florida: Cengage Learning.
- Smith, S. A. (2000). Algebra. Pearson Uddannelse.
- Vigil, C. (2015). Algebra og dets applikationer.



Endnu ingen kommentarer