EN empirisk regel Det er resultatet af praktisk erfaring og observation i det virkelige liv. For eksempel er det muligt at vide, hvilke fuglearter der kan observeres visse steder på hver tid af året, og ud fra denne observation kan der etableres en "regel", der beskriver livscyklussen for disse fugle.
I statistikker henviser den empiriske regel til den måde, hvorpå observationer er grupperet omkring en central værdi, middelværdien eller gennemsnittet, i enheder med standardafvigelse..
Antag at du har en gruppe mennesker med en gennemsnitshøjde på 1,62 meter og en standardafvigelse på 0,25 meter, så vil den empiriske regel give dig mulighed for at definere for eksempel, hvor mange mennesker der vil være i et interval på middel plus eller minus en standardafvigelse?
Ifølge reglen er 68% af dataene mere eller mindre en standardafvigelse fra gennemsnittet, dvs. 68% af befolkningen i gruppen vil have en højde mellem 1,37 (1,62-0,25) og 1,87 (1,62 + 0,25) meter.
Artikelindeks
Den empiriske regel er en generalisering af Tchebyshev-sætningen og den normale fordeling.
Tchebyshevs sætning siger, at: for en eller anden værdi af k> 1 er sandsynligheden for, at en tilfældig variabel falder mellem middelværdien minus k gange standardafvigelsen og gennemsnittet plus k gange, standardafvigelsen er større end eller lig med (1 - 1 / kto).
Fordelen ved denne sætning er, at den gælder for diskrete eller kontinuerlige tilfældige variabler med enhver sandsynlighedsfordeling, men den definerede regel ud fra den er ikke altid særlig præcis, da den afhænger af fordelingssymmetrien. Jo mere skæv fordelingen af den tilfældige variabel er, jo mindre justeret til reglen vil dens adfærd være.
Den empiriske regel defineret ud fra denne sætning er:
Hvis k = √2, siges det, at 50% af dataene er i intervallet: [µ - √2 s, µ + √2 s]
Hvis k = 2, siges det, at 75% af dataene er i intervallet: [µ - 2 s, µ + 2 s]
Hvis k = 3, siges det, at 89% af dataene er i intervallet: [µ - 3 s, µ + 3 s]
Normalfordelingen eller Gaussisk klokke gør det muligt at etablere den empiriske regel eller regel 68 - 95 - 99,7.
Reglen er baseret på sandsynligheden for forekomst af en tilfældig variabel i intervaller mellem gennemsnittet minus en, to eller tre standardafvigelser og gennemsnittet plus en, to eller tre standardafvigelser..
Den empiriske regel definerer følgende intervaller:
68,27% af dataene er i intervallet: [µ - s, µ + s]
95,45% af dataene er i intervallet: [µ - 2s, µ + 2s]
99,73% af dataene er i intervallet: [µ - 3s, µ + 3s]
I figuren kan du se, hvordan disse intervaller præsenteres, og forholdet mellem dem, når du øger bredden af grafens basis.
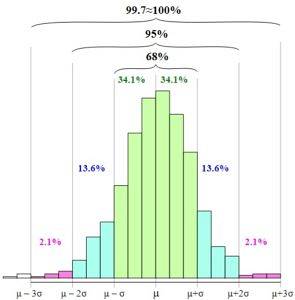
Derfor definerer anvendelsen af den empiriske regel i skala af en standard normalvariabel, z, følgende intervaller:
68,27% af dataene er i intervallet: [-1, 1]
95,45% af dataene er i intervallet: [-2, 2]
99,73% af dataene er i intervallet: [-3, 3]
Den empiriske regel tillader forkortede beregninger, når man arbejder med en normalfordeling.
Antag, at en gruppe på 100 universitetsstuderende har en gennemsnitsalder på 23 år med en standardafvigelse på 2 år. Hvilke oplysninger tillader den empiriske regel?
Anvendelse af den empiriske regel indebærer følgende trin:
Da gennemsnittet er 23, og standardafvigelsen er 2, er intervallerne:
[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]
[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]
[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]
(100) * 68,27% = cirka 68 studerende
(100) * 95,45% = ca. 95 studerende
(100) * 99,73% = ca. 100 studerende
Mindst 68 studerende er mellem 21 og 25 år.
Mindst 95 studerende er mellem 19 og 27 år.
Næsten 100 studerende er mellem 17 og 29 år.
Den empiriske regel er en hurtig og praktisk måde at analysere statistiske data på, bliver mere og mere pålidelig, når fordelingen nærmer sig symmetri.
Dens anvendelighed afhænger af det felt, det bruges i, og de spørgsmål, der præsenteres. Det er meget nyttigt at vide, at forekomsten af værdier af tre standardafvigelser under eller over gennemsnittet er næsten usandsynlig, selv for ikke-normale fordelingsvariabler, mindst 88,8% af tilfældene er i intervallet tre sigma.
I samfundsvidenskaben er et generelt afgørende resultat intervallet af middel plus eller minus to sigma (95%), mens i partikelfysik kræver en ny effekt et fem sigma-interval (99,99994%) for at blive betragtet som en opdagelse..
I et naturreservat anslås det, at der gennemsnitligt er 16.000 kaniner med en standardafvigelse på 500 kaniner. Hvis fordelingen af variablen 'antal kaniner i reserven' er ukendt, er det muligt at estimere sandsynligheden for, at kaninpopulationen er mellem 15.000 og 17.000 kaniner?
Intervallet kan præsenteres i disse vilkår:
15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s
17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s
Derfor: [15000, 17000] = [µ - 2 s, µ + 2 s]
Ved anvendelse af Tchebyshevs sætning er der en sandsynlighed på mindst 0,75 for, at kaninpopulationen i naturreservatet er mellem 15.000 og 17.000 kaniner..
Den gennemsnitlige vægt af et-årige børn i et land fordeles normalt med et gennemsnit på 10 kg og en standardafvigelse på ca. 1 kg.
a) Anslå procentdelen af etårige børn i landet, der har en gennemsnitlig vægt på mellem 8 og 12 kg.
8 = 10 - 2 = 10 - 2 (1) = µ - 2 s
12 = 10 + 2 = 10 + 2 (1) = µ + 2 s
Derfor: [8, 12] = [µ - 2s, µ + 2s]
Ifølge den empiriske regel kan det fastslås, at 68,27% af et-årige børn i landet har mellem 8 og 12 kg vægt.
b) Hvad er sandsynligheden for at finde et årigt barn, der vejer 7 kg eller derunder?
7 = 10 - 3 = 10 - 3 (1) = µ - 3 s
Det er kendt, at 7 kg vægt repræsenterer værdien µ - 3s, såvel som det er kendt, at 99,73% af børnene er mellem 7 og 13 kg. Det efterlader kun 0,27% af det samlede antal børn i ekstremiteterne. Halvdelen af dem, 0,355%, er 7 kg eller derunder, og den anden halvdel, 0,135%, er 11 kg eller mere.
Så det kan konkluderes, at der er en sandsynlighed på 0,00135, at et barn vejer 7 kg eller derunder.
c) Hvis landets befolkning når 50 millioner indbyggere, og 1-årige børn repræsenterer 1% af landets befolkning, hvor mange et-årige børn vil veje mellem 9 og 11 kg?
9 = 10 - 1 = µ - s
11 = 10 + 1 = µ + s
Derfor: [9, 11] = [µ - s, µ + s]
Ifølge den empiriske regel er 68,27% af etårige i landet i intervallet [µ - s, µ + s]
Der er 500.000 etårige i landet (1% af 50 millioner), så 341.350 børn (68,27% af 500.000) vejer mellem 9 og 11 kg.
Endnu ingen kommentarer