
Forhold og funktioner

Det matematisk forhold er det link, der findes mellem elementerne i en delmængde med hensyn til produktet af to sæt. EN fungere involverer den matematiske operation for at bestemme værdien af en afhængig variabel baseret på værdien af en uafhængig variabel. Hver funktion er en relation, men ikke enhver relation er en funktion.
| Forhold | Fungere | |
|---|---|---|
| Definition | Delsæt af bestilte par, der svarer til det kartesiske produkt af to sæt. | Matematisk operation, der skal udføres med variablen x for at få variablen Y. |
| Notation | x R Y; x det er relateret til Y. | Y= ƒ (x); Y er en funktion af x. |
| Egenskaber |
|
|
| Eksempler |
|
|
Hvad er et matematisk forhold?
Det kaldes det binære forhold for et sæt A i et sæt B eller forholdet mellem elementerne i A og B til hver delmængde C af det kartesiske produkt A x B.
Det vil sige, at hvis sæt A består af element 1, 2 og 3, og sæt B består af element 4 og 5, vil det kartesiske produkt af A x B være de bestilte par:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
Delsættet C = (2,4), (3,5) vil være et forhold mellem A og B, da det er sammensat af de ordnede par (2,4) og (3, 5), resultatet af den kartesiske produkt af A x B.
Forholdskoncept
"Lad A og B være to ikke-tomme sæt, lad A x B være produktsættet for begge, det vil sige: A x B er dannet af de ordnede par (x, y) således at x er elementet i A og Y det er for B. Hvis en delmængde C er defineret i A x B, bestemmes en binær relation i A og B automatisk som følger:
x R Y hvis og kun hvis (x, y) ∈ C
(notationen x R Y Midler "x det er relateret til Y").
Vi kalder sæt A start sæt og vi kalder sæt B ankomst sæt.
Det forholdsdomæne er de elementer, der udgør startsættet, mens forholdsområde er elementerne i ankomstsættet.
Eksempel på matematiske forhold
Sæt TIL fra x elementer af mænd i en befolkning og B er sæt af Y elementer af kvinder fra samme befolkning. Et forhold oprettes, når "x er gift med Y".
Hvad er en matematisk funktion?
Når vi taler om en matematisk funktion af et sæt A i et sæt B henviser vi til en regel eller mekanisme, der relaterer elementerne i sæt A med et element i sæt B.
Funktionskoncept
"Sean x Y Y to reelle variabler, så siges det så y er en funktion af x ja til hver værdi, jeg tager x svarer til en værdi på Y."
Den uafhængige variabel er x mens Y er den afhængige variabel eller funktion:
y = ƒ (x)
Sættet, hvori x det kaldes funktionens domæne (original) og variationen af Y funktionsområde (billede).
Sættet af par (x, Y) sådan at Y= ƒ (x) Hedder funktionsgraf; hvis de er repræsenteret i kartesiske akser, opnås en familie af punkter kaldet funktionsgraf.
Funktionseksempler
I matematik får vi mange eksempler på funktioner. Her er eksempler på flagskibsfunktioner.
Konstant funktion
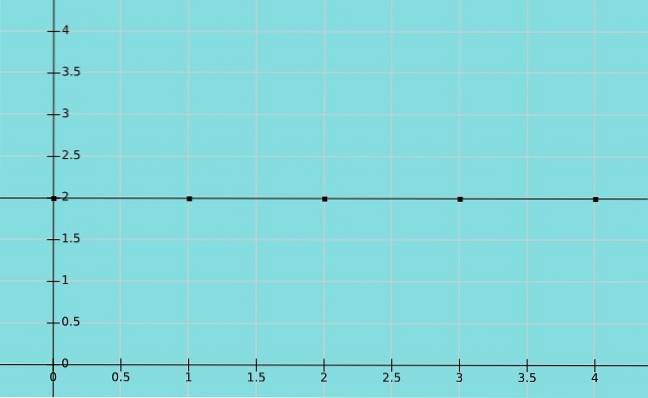
En funktion kaldes konstant, hvis elementet i sæt B, der svarer til sæt A, er det samme. I dette tilfælde svarer alle værdierne til x til den samme værdi af y. Således er domænet de reelle tal, mens området er en konstant værdi.
Identitetsfunktion
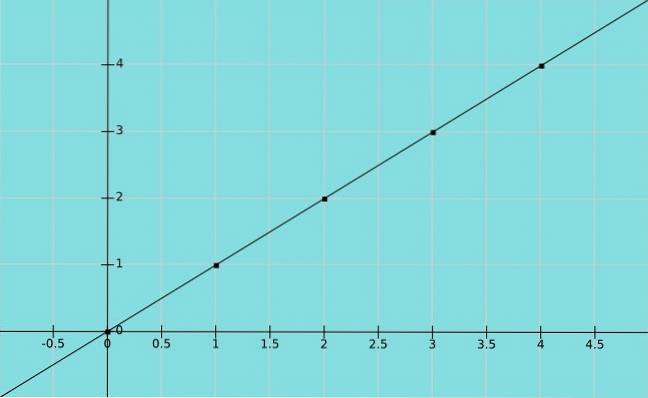
Lad os antage det x er en variabel og det Y tager den samme værdi som x. Vi har derefter en identitetsfunktion y = x, hvor parenex, y) i grafen er (1,1), (2,2), (3,3) og så videre.
Polynomial funktion

En polynomfunktion opfylder formen y = anxn+tiln-1+xn-1+… + Atoxto+til1x + a0. Grafen ovenfor viser funktionen ƒ (x) = xto+x-2.
Antag nu, at den afhængige variabel Y er lig med den uafhængige variabel x hævet til terningen. Vi har funktionen y = x3, hvis graf er vist nedenfor:
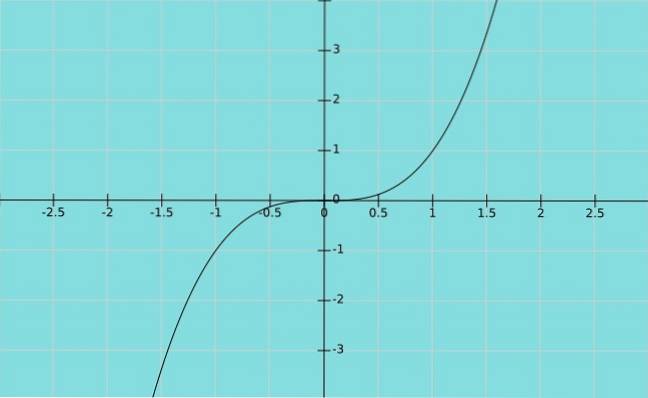


Endnu ingen kommentarer