To punkter A og A har central symmetri med hensyn til et punkt O, når segmentet AA 'passerer gennem det og også er midtpunktet for AA'. Punkt O kaldes centrum for symmetri.
Den centrale symmetri for en trekant ABC i forhold til et punkt O er en anden trekant A'B'C ', der har følgende egenskaber:
-Homologe segmenter har samme længde
-Deres tilsvarende vinkler har samme mål.
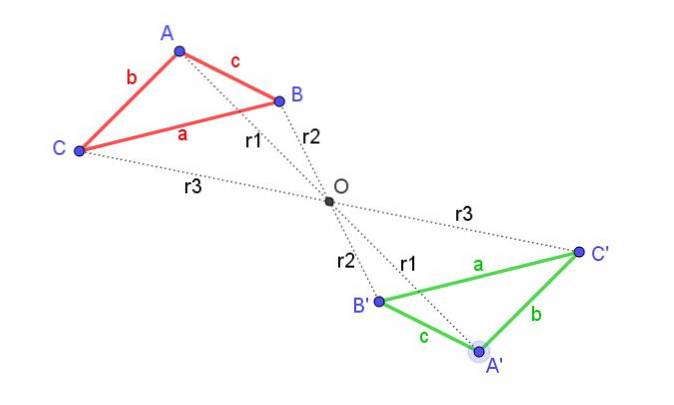
I figur 1 kan du se en trekant ABC (rød) og dens centrale symmetri A'B'C '(grøn) i forhold til centrum for symmetri O.
I den samme figur ville en opmærksom observatør indse, at det samme resultat opnås ved at anvende en rotation af den oprindelige trekant, så længe den er 180 ° og er centreret i O.
Derfor svarer en central symmetri til en 180 ° drejning i forhold til symmetriens centrum.
Artikelindeks
En central symmetri har følgende egenskaber:
-Centeret for symmetri er midtpunktet i det segment, der forbinder et punkt med dets symmetri.
-Et symmetrisk punkt for et andet, der er placeret i centrum af symmetri, falder sammen med centrum for symmetri.
-Den centrale symmetri af en trekant er en trekant, der er kongruent (lig) med originalen.
-Billedet ved central symmetri af en cirkel er en anden cirkel med lige radius.
-En cirkel har central symmetri om sit eget centrum.
-Ellipsen har central symmetri omkring dens centrum.
-Et segment har central symmetri omkring dets midtpunkt.
-Den ligesidede trekant har ikke central symmetri i forhold til dens centrum, fordi dens symmetri, skønt den er kongruent med den første, giver en roteret ligesidet trekant.
-Kvadrater har central symmetri omkring deres centrum.
-En femkant mangler central symmetri omkring dens centrum.
-Regelmæssige polygoner har central symmetri, når de har et lige antal sider.
Symmetri-kriterier har mange anvendelser inden for videnskab og teknik. Central symmetri er til stede i naturen, for eksempel har iskrystaller og spindelvæv denne form for symmetri.
Desuden løses mange problemer let, når eksistensen af central symmetri og andre former for symmetri udnyttes. Derfor er det praktisk at hurtigt identificere, hvornår det sker.
Givet et punkt P af koordinater (a, b), skal vi finde koordinaterne for dets symmetriske P 'med hensyn til oprindelsen O for koordinater (0, 0).
Den første ting er at konstruere punktet P ', for hvilket der tegnes en linje, der passerer gennem oprindelsen O og gennem punktet P. Ligningen af linjen er y = (b / a) x.
Lad os nu kalde (a ', b') koordinaterne for det symmetriske punkt P '. Punktet P 'skal ligge på linjen, der passerer gennem O, og derfor er det sandt: b' = (b / a) a '. Desuden skal afstanden OP være lig med OP ', som i analytisk form skrives således:
√ (tilto + bto) = √ (a 'to + b 'to )
Det følgende er at erstatte b '= [(b / a) .a'] i ovenstående udtryk og kvadratere begge sider af ligestillingen for at eliminere kvadratroden: (ato + bto) = [a 'to + (bto/tilto).til'to]
Ved at udtrække fælles faktor og forenkle, får vi det en 'to = ato. Denne ligning har to reelle løsninger: a '= + a eller a' = -a.
For at få b 'bruger vi igen b' = (b / a) a '. Hvis den positive løsning af a 'erstattes, når vi frem til det b' = b. Og når den negative opløsning er substitueret, så er b '= -b.
Den positive løsning giver for P 'det samme punkt P, så det kasseres. Den negative løsning giver bestemt koordinaterne for det symmetriske punkt:
P ': (-a, -b)
Det kræves at vise, at et segment AB og dets centrale symmetriske A'B 'har samme længde.
Begyndende med koordinaterne for punkt A, som er (Ax, Ay) og de for punkt B: (Bx, By), er længden af segment AB givet ved:
d (AB) = √ ((Bx - Ax)to + (Af - Ay)to )
Analogt vil det symmetriske segment A'B 'have længden givet ved:
d (A'B ') = √ ((Bx' - Ax ')to + (Af '- Ay')to )
Koordinaterne for det symmetriske punkt A 'er Ax' = -Ax og Ay '= -Ay. Tilsvarende er de af B 'Bx' = -Bx og By '= -By. Hvis disse koordinater er substitueret i ligningen af afstanden d (A'B ') har vi:
d (A'B ') = √ ((-Bx + Ax)to + (-By + Ay)to), der svarer til:
√ ((Bx - Ax)to + (Af - Ay)to) = d (AB)
Således vises, at begge segmenter har samme længde.
Vis analytisk, at den centrale symmetriske O i en cirkel med radius R og centrum O er den samme originale cirkel.
Ligningen af en cirkel med radius R og centrum O (0,0) er:
xto + Yto = Rto (Ligning af omkredsen C)
Hvis der ved hvert punkt P i omkredsen y af koordinaterne (x, y) findes dens symmetriske P 'af koordinaterne (x', y '), er ligningen af den symmetriske omkreds:
x 'to + Y 'to = Rto (Ligning af den symmetriske cirkel C ')
Nu henviser vi til resultatet af eksempel 1, hvor det konkluderes, at koordinaterne for et punkt P ', symmetrisk til P og med koordinater (a, b), er (-a, -b).
Men i denne øvelse har punkt P koordinater (x, y), så dets symmetriske P 'vil have koordinater x' = -x og y '= -y. Ved at erstatte dette i ligningen af den symmetriske cirkel har vi:
(-x)to + (-Y)to = Rto
Hvilket svarer til: xto+ Yto = Rto, konkluderer, at den centrale symmetri af en cirkel i forhold til dens centrum er selve omkredsen.
Vis geometrisk, at central symmetri bevarer vinkler.
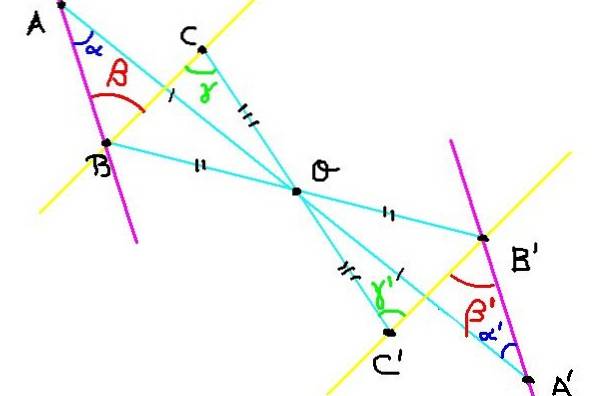
Der er tre punkter A, B og C på flyet. Dens symmetri A ', B' og C 'er konstrueret i forhold til centrum for symmetri O, som vist i figur 4.
Nu skal vi vise, at vinklen ∡ABC = β har samme mål som vinklen ∡A'B'C '= β'.
Da C og C 'er symmetriske, er OC = OC'. Tilsvarende OB = OB 'og OA = OA'. På den anden side er vinklen ∡BOC = ∡B'OC ', fordi de er modsat af toppunktet.
Derefter er trekanterne BOC og B'OC 'kongruente, fordi de har en lige vinkel mellem to lige sider.
Da BOC er kongruent til B'OC ', så er vinklerne γ Y γ ' De er lige. Men disse vinkler ud over at opfylde γ = γ ' er interne veksler mellem linierne BC og B'C ', hvilket indebærer, at linjen BC er parallel med B'C'.
På samme måde er BOA kongruent med B'OA ', hvorfra det følger α = α ' . Men a Y α ' er alternative indvendige vinkler mellem linjer BA og B'A ', hvorfra det konkluderes, at linje BA er parallel med B'A'.
Da vinklen ∡ABC = β har siderne parallelle med vinklen ∡A'B'C '= β' og begge er akutte, konkluderes det at:
∡ABC = ∡A'B'C '= β = β'
Beviser på denne måde, at den centrale symmetri bevarer vinklenes mål.
Endnu ingen kommentarer