
Summen af polynomer, hvordan man gør det, eksempler, øvelser
Det sum af polynomer er den operation, der består i at tilføje to eller flere polynomier, hvilket resulterer i et andet polynom. For at udføre det er det nødvendigt at tilføje vilkårene i den samme rækkefølge for hver af polynomierne og angive den resulterende sum.
Lad os først kort gennemgå betydningen af "vilkår i samme rækkefølge." Ethvert polynom består af tilføjelser og / eller subtraktioner af termer.

Udtrykkene kan være produkter med reelle tal og en eller flere variabler, repræsenteret af bogstaver, for eksempel: 3xto og -√5.atobc3 er vilkår.
Vilkårene for den samme rækkefølge er dem, der har den samme eksponent eller magt, selvom de kan have en anden koefficient.
-Lige ordrebetingelser er: 5x3, √2 x3 og -1 / 2x3
-Forskellige ordrebetingelser: -2x-to, 2xy-1 og √6xtoY
Det er vigtigt at huske på, at kun vilkår i samme rækkefølge kan tilføjes eller trækkes fra, en operation kendt som reduktion. Ellers er summen blot angivet.
Når begrebet udtryk i samme rækkefølge er blevet afklaret, tilføjes polynomierne ved at følge disse trin:
-Bestille Først de polynomer, der skal tilføjes, alt på samme måde, enten på en stigende eller faldende måde, det vil sige med kræfterne fra lavere til højere eller omvendt.
-At færdiggøre, hvis der mangler strøm i sekvensen.
-Reducere lignende vilkår.
-Angive den resulterende sum.
Artikelindeks
- 1 Eksempler på tilføjelse af polynomer
- 1.1 Tilføj to eller flere polynomer med mere end en variabel
- 2 Øvelser til tilføjelse af polynomer
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referencer
Eksempler på tilføjelse af polynomer
Vi starter med at tilføje to polynomer med en enkelt variabel kaldet x, for eksempel polynomierne P (x) og Q (x) givet af:
P (x) = 2xto - 5x4 + 2x -x5 - 3x3 +12
Q (x) = x5- 25 x + xto
Efter de beskrevne trin starter du med at bestille dem i faldende rækkefølge, hvilket er den mest almindelige måde:
P (x) = -x5- 5x4 - 3x3 + 2xto + 2x +12
Q (x) = x5+ xto - 25x
Polynomet Q (x) er ikke komplet, man ser, at der mangler kræfter med eksponenterne 4, 3 og 0. Sidstnævnte er simpelthen det uafhængige udtryk, det, der ikke har noget bogstav.
Q (x) = x5+ 0x4 + 0x3 + xto - 25x + 0
Når dette trin er gjort, er de klar til at tilføje. Du kan tilføje lignende vilkår og derefter angive summen eller placere de ordnede polynomer under hinanden og reducere med kolonner på denne måde:
- x5 - 5x4 - 3x3 + 2xto + 2x +12
+ x5 + 0x4 + 0x3 + xto - 25x + 0 +
--
0x5-5x4 - 3x3 +3xto - 23x + 12 = P (x) + Q (x)
Det er vigtigt at bemærke, at når det tilføjes, gøres det algebraisk under overholdelse af tegnreglen, på denne måde 2x + (-25 x) = -23x. Det vil sige, hvis koefficienterne har et andet tegn, trækkes de, og resultatet bærer tegnet på det større.
Tilføj to eller flere polynomer med mere end en variabel
Når det kommer til polynomer med mere end en variabel, vælges en af dem til at bestille den. Antag for eksempel, at du beder om at tilføje:
R (x, y) = 5xto - 4yto + 8xy - 6y3
Y:
T (x, y) = ½ xto- 6yto - 11xy + x3Y
En af variablerne er valgt, for eksempel x for at bestille:
R (x, y) = 5xto + 8xy - 6y3 - 4yto
T (x, y) = + x3y + ½ xto - 11xy - 6 årto
Umiddelbart afsluttes de manglende udtryk, ifølge hvilke hvert polynom har:
R (x, y) = 0x3y + 5xto + 8xy - 6y3 - 4yto
T (x, y) = + x3y + ½ xto - 11xy + 0y3 - 6yto
Og I er begge klar til at reducere lignende vilkår:
0x3y + 5xto + 8xy - 6y3 - 4yto
+ x3y + ½ xto - 11xy + 0y3 - 6 årto +
-
+ x3og + 11 / 2xto - 3xy - 6 år3 - 10 årto = R (x, y) + T (x, y)
Polynomiske øvelser
- Øvelse 1
I den følgende sum af polynomer skal du angive det udtryk, der skal gå i det tomme rum for at opnå polynomsummen:
-5x4 + 0x3 + 2xto + 1
x5 + 2x4 - 21xto + 8x - 3
2x5 +9x3 -14x
-
-6x5+10x4 -0x3 + 5xto - 11x + 21
Opløsning
For at få -6x5 der kræves et udtryk for formen økse5, sådan at:
a + 1+ 2 = -6
Derfor:
a = -6-1-2 = -9
Og søgeudtrykket er:
-9x5
-Fortsæt på en lignende måde for at finde resten af vilkårene. Her er den til eksponent 4:
-5 + 2 + a = 10 → a = 10 + 5-2 = 13
Det manglende udtryk er: 13x4.
-For kræfterne i x3 det er øjeblikkeligt, at udtrykket skal være -9x3, således er koefficienten for det kubiske udtryk 0.
-Med hensyn til de kvadrerede kræfter: a + 8 - 14 = -11 → a = -11 - 8 + 14 = -5 og udtrykket er -5 xto.
-Det lineære udtryk opnås ved hjælp af en +8 -14 = -11 → a = -11 + 14 - 8 = -5, hvor den manglende betegnelse er -5x.
-Endelig er det uafhængige udtryk: 1 -3 + a = -21 → a = -19.
- Øvelse 2
Et fladt terræn er indhegnet som vist i figuren. Find et udtryk for:
a) Omkredsen og
b) Dets areal i form af de angivne længder:
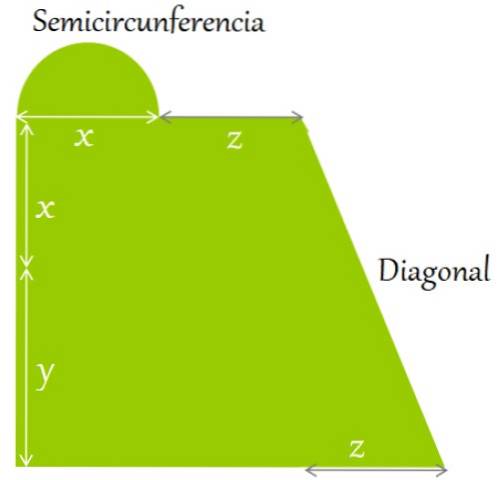
Løsning til
Omkredsen er defineret som summen af siderne og konturerne af figuren. Startende i nederste venstre hjørne med uret har vi:
Omkreds = y + x + halvcirkel længde + z + diagonal længde + z + z + x
Halvcirklen har en diameter lig med x. Da radius er halv diameter, skal vi:
Radius = x / 2.
Formlen for længden af en komplet omkreds er:
L = 2π x Radius
Derefter:
Halvcirkelens længde = ½. 2π (x / 2) = πx / 2
For sin del beregnes diagonalen med Pythagoras sætning anvendt på siderne: (x + y), som er den lodrette side og z, som er den vandrette:
Diagonal = [(x + y)to + zto]1/2
Disse udtryk er erstattet i en med omkredsen for at opnå:
Omkreds = y + x + πx / 2 + z + [(x + y)to + zto]1/2+ z + x + z
Lignende vilkår reduceres, da tilføjelsen kræver, at resultatet forenkles så meget som muligt:
Omkreds = y + [x + π (x / 2) + x] + z + z + z + [(x + y)to + zto]1/2 = y + (2 + π / 2) x + 3z
Løsning b
Det resulterende område er summen af arealet af rektanglet, halvcirklen og den højre trekant. Formlerne for disse områder er:
-Rektangel: base x højde
-Halvcirkel: ½ π (Radius)to
-Trekant: bund x højde / 2
Rektangelområde
(x + y). (x + z) = xto + xz + yx + yz
Halvcirkelområde
½ π (x / 2)to = π xto / 8
Trekantsområde
½ z (x + y) = ½ zx + ½ zy
Samlet areal
For at finde det samlede areal tilføjes de fundne udtryk for hvert delområde:
Samlet areal = xto + xz + yx + yz + (π xto / 8) + ½ zx + ½ zy
Og til sidst reduceres alle de udtryk, der ligner hinanden:
Samlet areal = (1 + π / 8) xto + 3/2 xy + 3 / 2yz + yx
Referencer
- Baldor, A. 1991. Algebra. Redaktionel Cultural Venezolana S.A.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematik er sjovt. Tilføjelse og fratrækning af polynomer. Gendannet fra: mathsisfun.com.
- Monterey Institute. Tilføjelse og fratrækning af polynomer. Gendannet fra: montereyinstitute.org.
- UC Berkeley. Algebra af polynomer. Gendannet fra: math.berkeley.edu.



Endnu ingen kommentarer