
Bayes sætning forklaring, applikationer, øvelser
Det Bayes sætning er en procedure, der giver os mulighed for at udtrykke den betingede sandsynlighed for en tilfældig begivenhed A givet B med hensyn til sandsynlighedsfordelingen af begivenhed B givet A og sandsynlighedsfordelingen kun A.
Denne sætning er meget nyttig, da takket være den kan vi relatere sandsynligheden for, at en begivenhed A opstår, idet vi ved, at B opstod, med sandsynligheden for, at det modsatte sker, det vil sige, at B forekommer givet A.
Bayes 'sætning var et sølvforslag fra præsten Thomas Bayes, en engelsk teolog fra det 18. århundrede, som også var matematiker. Han var forfatter til adskillige værker i teologi, men på nuværende tidspunkt er han kendt for et par matematiske afhandlinger, blandt hvilke den allerede nævnte Bayes sætning skiller sig ud som hovedresultatet.
Bayes behandlede denne sætning i et værk med titlen "Et essay mod løsning af et problem i læren om chancer", udgivet i 1763, og som der er udviklet et stort antal studier med applikationer inden for forskellige vidensområder..
Artikelindeks
- 1 Forklaring
- 2 Anvendelser af Bayes 'sætning
- 2.1 Løste øvelser
- 3 Referencer
Forklaring
For at få en bedre forståelse af denne sætning er det grundlæggende nødvendigt med nogle grundlæggende forestillinger om sandsynlighedsteori, især multiplikationsteoremet for betinget sandsynlighed, som siger, at
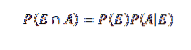
For E og A vilkårlige begivenheder i et prøveområde S.
Og definitionen af partitioner, som fortæller os, at hvis vi har A1 ,TILto,… , TILn begivenheder i et prøveområde S, vil disse danne en partition af S, hvis Ajeg udelukker hinanden gensidigt, og deres forening er S.
I betragtning af dette, lad B være en anden begivenhed. Så vi kan se B som
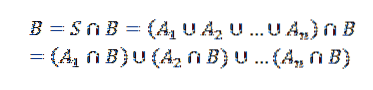
Hvor Ajeg krydset med B er gensidigt eksklusive begivenheder.
Og som konsekvens,
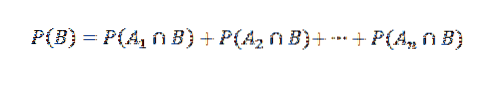
Anvend derefter multiplikationssætningen
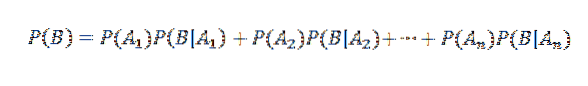
På den anden side er den betingede sandsynlighed for Ai givet B defineret af
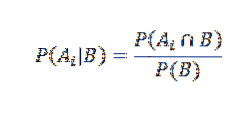
Udskiftning passende Vi har det for enhver i
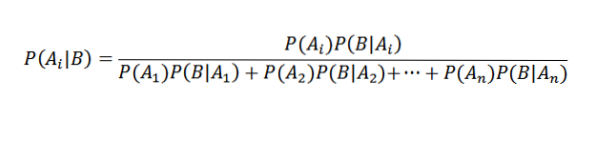
Anvendelser af Bayes 'sætning
Takket være dette resultat har forskergrupper og forskellige virksomheder formået at forbedre systemer, der er baseret på viden..
F.eks. Kan Bayes 'sætning i undersøgelsen af sygdomme hjælpe med at skelne sandsynligheden for, at en sygdom findes i en gruppe mennesker med en given egenskab, idet de tager som data sygdommens samlede hastighed og dominansen af de nævnte egenskaber i begge raske og syge mennesker.
På den anden side har det i verden med høje teknologier påvirket store virksomheder, der takket være dette resultat har udviklet "vidensbaseret" software.
Som et dagligt eksempel har vi Microsoft Office-assistenten. Bayes 'sætning hjælper softwaren med at evaluere de problemer, som brugeren præsenterer, og bestemme, hvilken rådgivning de skal levere og dermed være i stand til at tilbyde en bedre service i henhold til brugerens vaner.
Det skal bemærkes, at denne formel blev ignoreret indtil for nylig, dette er hovedsageligt fordi da dette resultat blev udviklet for 200 år siden, var der kun lidt praktisk brug af dem. Imidlertid har forskere i vores tid takket være store teknologiske fremskridt fundet måder at omsætte dette resultat til.
Løst øvelser
Øvelse 1
Et mobiltelefonfirma har to maskiner A og B. 54% af de producerede mobiltelefoner er fremstillet af maskine A og resten af maskine B. Ikke alle producerede mobiltelefoner er i god stand.
Andelen af defekte mobiltelefoner fremstillet af A er 0,2 og af B er 0,5. Hvad er sandsynligheden for, at en mobiltelefon fra fabrikken er defekt? Hvad er sandsynligheden for, at den, der vides at en mobiltelefon er defekt, kommer fra maskine A?
Opløsning
Her har du et eksperiment, der udføres i to dele; i første del forekommer begivenhederne:
A: celle fremstillet af maskine A.
B: celle fremstillet af maskine B.
Da maskine A producerer 54% af mobiltelefoner, og resten produceres af maskine B, følger det derfor, at maskine B producerer 46% af mobiltelefoner. Sandsynligheden for disse begivenheder er angivet, nemlig:
P (A) = 0,54.
P (B) = 0,46.
Begivenhederne i anden del af eksperimentet er:
D: defekt mobiltelefon.
E: ikke-defekt mobiltelefon.
Som anført i erklæringen afhænger sandsynligheden for disse begivenheder af resultatet opnået i første del:
P (D | A) = 0,2.
P (D | B) = 0,5.
Ved hjælp af disse værdier kan sandsynligheden for komplementerne til disse begivenheder også bestemmes, det vil sige:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
Y
p (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Nu kan begivenhed D skrives som følger:
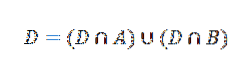
Brug af multiplikationssætningen til resultater med betinget sandsynlighed:
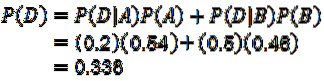
Med hvilket det første spørgsmål besvares.
Nu skal vi kun beregne P (A | D), som Bayes-sætningen anvendes til:
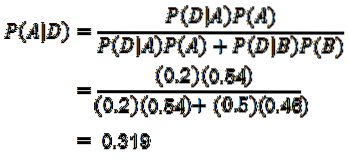
Takket være Bayes 'sætning kan det fastslås, at sandsynligheden for, at en mobiltelefon er lavet af maskine A, vel vidende, at mobiltelefonen er defekt, er 0,319.
Øvelse 2
Tre kasser indeholder sorte og hvide kugler. Sammensætningen af hver af dem er som følger: U1 = 3B, 1N, U2 = 2B, 2N, U3 = 1B, 3N.
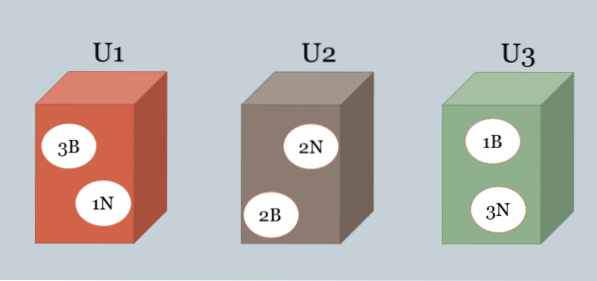
Et af felterne vælges tilfældigt, og en bold trækkes tilfældigt, som viser sig at være hvid. Hvad er den boks, der mest sandsynligt er blevet valgt?
Opløsning
Ved hjælp af U1, U2 og U3 repræsenterer vi også det valgte felt.
Disse begivenheder udgør en partition af S, og det er verificeret, at P (U1) = P (U2) = P (U3) = 1/3, da valget af felt er tilfældigt.
Hvis B = den trukkede kugle er hvid, har vi P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
Det, vi ønsker at opnå, er sandsynligheden for, at bolden er taget ud af feltet Ui vel vidende, at bolden var hvid, det vil sige P (Ui | B), og se hvilken af de tre værdier, der var den højeste at vide hvoraf boksen sandsynligvis har været udvinding af den hvide kugle.
Anvendelse af Bayes sætning på den første af felterne:
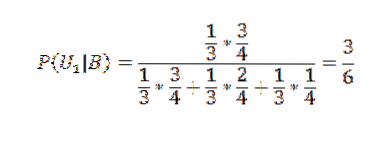
Og for de to andre:
P (U2 | B) = 2/6 og P (U3 | B) = 1/6.
Derefter er den første af boksene den med størst sandsynlighed for at være valgt til udvinding af den hvide kugle..
Referencer
- Kai Lai Chung. Elementær sandsynlighedsteori med stokastiske processer. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskret matematik og dens anvendelser. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sandsynlighed og statistiske anvendelser. S.A. MEXICAN ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Løste problemer med diskret matematik. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Problemer med teori og sandsynlighed. McGRAW-HILL.


Endnu ingen kommentarer