
Bernoullis sætningsligning, applikationer og løst øvelse
Det Bernoullis sætning, der beskriver en væskes opførsel i bevægelse, blev underkendt af matematikeren og fysikeren Daniel Bernoulli i hans arbejde Hydrodynamik. Ifølge princippet vil en ideel væske (uden friktion eller viskositet), der cirkulerer gennem en lukket ledning, have en konstant energi i sin vej.
Teoremet kan udledes af princippet om bevarelse af energi og endda fra Newtons anden bevægelseslov. Derudover fastslår Bernoullis princip også, at en stigning i en væskes hastighed indebærer et fald i det tryk, som den udsættes for, et fald i dens potentielle energi eller begge på samme tid..

Teoremet har mange forskellige anvendelser, både i videnskabens verden og i folks hverdag..
Dets konsekvenser er til stede i flyets løftekraft, i skorstene i hjem og industrier, i vandrør, blandt andre områder..
Artikelindeks
- 1 Bernoullis ligning
- 1.1 Forenklet form
- 2 applikationer
- 3 Øvelse løst
- 4 Referencer
Bernoullis ligning
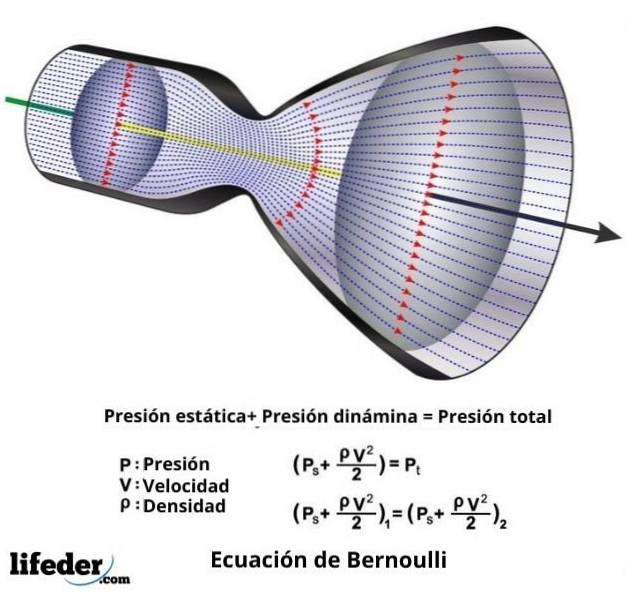
Selvom Bernoulli var den, der udledte, at trykket falder, når strømningshastigheden stiger, er sandheden, at det var Leonhard Euler, der faktisk udviklede Bernoulli-ligningen i den form, som den er kendt i dag..
Under alle omstændigheder er Bernoullis ligning, som ikke er andet end det matematiske udtryk for hans sætning, følgende:
vto ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = konstant
I dette udtryk er v væskens hastighed gennem det betragtede afsnit, ƿ er væskens tæthed, P er væskets tryk, g er værdien af tyngdeacceleration, og z er højden målt i tyngdekraftsretning.
Det er implicit i Bernoullis ligning, at energien i en væske består af tre komponenter:
- En kinetisk komponent, som er den, der skyldes den hastighed, hvormed væsken bevæger sig.
- En potentiel eller tyngdekomponent, der skyldes den højde, hvor væsken er.
- En trykenergi, som er den, som væsken besidder som en konsekvens af det tryk, den udsættes for.
På den anden side kan Bernoullis ligning også udtrykkes således:
v1 to ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtoto ∙ ƿ / 2 + Pto + ƿ ∙ g ∙ zto
Dette sidste udtryk er meget praktisk til at analysere de ændringer, som en væske oplever, når nogle af de elementer, der udgør ligningen, ændres.
Forenklet form
Ved visse lejligheder er ændringen i ρgz-begrebet i Bernoullis ligning minimal sammenlignet med den, der opleves af de andre udtryk, så den kan overses. For eksempel sker dette i strømme, der opleves af et fly under flyvning..

Ved disse lejligheder udtrykkes Bernoullis ligning som følger:
P + q = P0
I dette udtryk er q dynamisk tryk og svarer til v to ∙ ƿ / 2 og P0 er det, der kaldes total tryk og er summen af det statiske tryk P og det dynamiske tryk q.
Ansøgninger

Bernoullis sætning har mange og forskellige anvendelser inden for så forskellige områder som videnskab, teknik, sport osv..
En interessant applikation findes i designet af pejse. Skorstene er bygget højt for at opnå en større trykforskel mellem basen og skorstenens udløb, takket være hvilken det er lettere at ekstrahere forbrændingsgasserne.
Bernoullis ligning gælder selvfølgelig også for undersøgelse af bevægelse af væskestrømme i rør. Af ligningen følger det, at en reduktion i rørets tværsnitsareal for at øge hastigheden af væsken, der passerer gennem det, også indebærer et fald i tryk.
Bernoulli-ligningen bruges også i luftfart og i formel 1. Køretøjer. I tilfælde af luftfart er Bernoulli-effekten oprindelsen til løft af fly.
Flyvinger er designet med det mål at opnå større luftstrøm øverst på vingen.
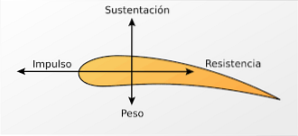
Således er lufthastigheden i den øverste del af vingen høj, og trykket er derfor lavere. Denne trykforskel producerer en lodret opadrettet kraft (løftekraft), der gør det muligt for flyet at svæve i luften. En lignende virkning opnås i kørebanerne i Formel 1-biler.
Træning løst
Gennem et rør med et tværsnit på 4,2 cmto en strøm af vand strømmer ved 5,18 m / s. Vandet ned fra en højde på 9,66 m til et lavere niveau med en højde på nul, mens rørets tværsnitsareal stiger til 7,6 cmto.
a) Beregn hastigheden på vandstrømmen på det lavere niveau.
b) Bestem trykket på det lavere niveau, vel vidende at trykket på det øverste niveau er 152000 Pa.
Opløsning
a) I betragtning af at strømmen skal bevares, er det rigtigt, at:
SpørgsmålØvre niveau = Qlavere niveau
v1 . S1 = vto . Sto
5,18 m / s. 4,2 cmto = vto . 7,6 cm ^to
Løsning for opnås, at:
vto = 2,86 m / s
b) Anvendelse af Bernoullis sætning mellem de to niveauer og under hensyntagen til, at tætheden af vand er 1000 kg / m3 , det opnås, at:
v1 to ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtoto ∙ ƿ / 2 + Pto + ƿ ∙ g ∙ zto
(1/2). 1000 kg / m3 . (5,18 m / s)to + 152000 + 1000 kg / m3 . 10 m / sto . 9,66 m =
= (1/2). 1000 kg / m3 . (2,86 m / s)to + Pto + 1000 kg / m3 . 10 m / sto . 0 m
Løsning for Pto du kommer til:
Pto = 257926,4 Pa
Referencer
- Bernoullis princip. (nd). På Wikipedia. Hentet den 12. maj 2018 fra es.wikipedia.org.
- Bernoullis princip. (nd). I Wikipedia. Hentet den 12. maj 2018 fra en.wikipedia.org.
- Batchelor, G.K. (1967). En introduktion til væskedynamik. Cambridge University Press.
- Lamb, H. (1993). Hydrodynamik (6. udgave). Cambridge University Press.
- Mott, Robert (1996). Anvendt væskemekanik (4. udgave). Mexico: Pearson Education.



Endnu ingen kommentarer