
Eksistens og unikhed sætning bevis, eksempler og øvelser
Det Eksistens og unikhedssætning fastlægger de nødvendige og tilstrækkelige betingelser, så en første ordens differentialligning med en given starttilstand har en løsning, og at denne løsning også er den eneste.
Teoremet giver dog ingen teknik eller indikation af, hvordan man finder en sådan løsning. Eksistens- og unikhedssætningen udvides også til højere ordens differentialligninger med indledende betingelser, som er kendt som Cauchy-problemet..
Den formelle erklæring om eksistens- og unikhedssætningen er som følger:
"For en differentialligning y '(x) = f (x, y) med oprindelig tilstand y (a) = b, eksisterer mindst en løsning i et rektangulært område af planet XY indeholder til punktet (a, b), Ja f (x, y) det er kontinuerligt i denne region. Og hvis den delvise afledte af F med respekt for Y: g = ∂f / ∂og er kontinuerlig i det samme rektangulære område, så er løsningen unik i et punkt af punktet (a, b) indhold i kontinuitetsregionen i F Y g."
Nytten af denne sætning ligger først i at vide, hvilke regioner i XY-planet, hvor en løsning kan eksistere, og også at vide, om den fundne løsning er den eneste mulige, eller om der er andre..
Bemærk, at hvis den unikke betingelse ikke er opfyldt, kan sætningen ikke forudsige, hvor mange løsninger i alt Cauchy-problemet har: måske er det en, to eller flere.
Artikelindeks
- 1 Bevis for eksistens- og unikhedssætningen
- 2 Eksempler
- 2.1 - Eksempel 1
- 2.2 - Eksempel 2
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Bevis for eksistens og unikhedssætning

Til denne sætning kendes to mulige beviser, den ene er beviset for Charles Émile Picard (1856-1941), og den anden skyldes Giuseppe Peano (1858-1932) baseret på værkerne fra Augustin Louis Cauchy (1789-1857 ).
Det er bemærkelsesværdigt, at de mest geniale matematiske sind i det nittende århundrede deltog i beviset for denne sætning, så det kan fortolkes, at ingen af de to er enkle.
For formelt at bevise sætningen er det nødvendigt først at etablere en række mere avancerede matematiske begreber, såsom funktioner af Lipschitz-typen, Banach-rum, Carathéodory's eksistenssætning og flere andre, som ligger uden for artiklens anvendelsesområde..
En stor del af de differentialligninger, der håndteres i fysik, beskæftiger sig med kontinuerlige funktioner i regionerne af interesse, derfor begrænser vi os til at vise, hvordan sætningen anvendes i enkle ligninger.
Eksempler
- Eksempel 1
Lad os overveje følgende differentialligning med en indledende tilstand:
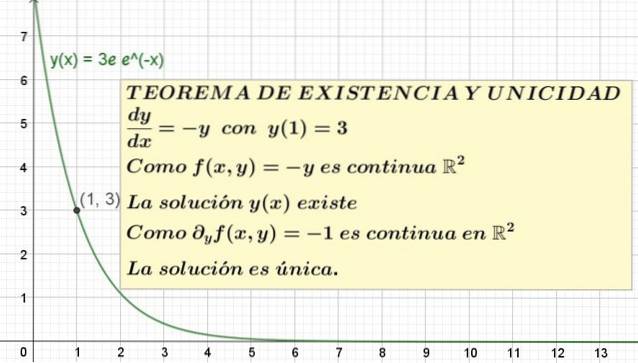
y '(x) = - y; med y (1) = 3
Er der en løsning på dette problem? Er det den eneste mulige løsning?
Svar
For det første evalueres eksistensen af løsningen af differentialligningen, og at den også opfylder den oprindelige betingelse.
I dette eksempel f (x, y) = - y eksistensbetingelsen kræver at vide, om f (x, y) er kontinuerlig i en region af planet XY der indeholder punktet for koordinaterne x = 1, y = 3.
Men f (x, y) = - y er affin funktion, som er kontinuerlig inden for domænet for reelle tal og findes i hele rækkevidden af reelle tal.
Derfor konkluderes det, at f (x, y) er kontinuerlig i Rto, så sætningen garanterer eksistensen af mindst én løsning.
Når man ved dette, er det nødvendigt at evaluere, om løsningen er unik, eller om der tværtimod er mere end en. Til dette er det nødvendigt at beregne delderivatet af F med hensyn til variablen Y:
∂f / ∂y = ∂ (-y) / ∂y = -1
Derefter g (x, y) = -1 som er en konstant funktion, som også er defineret for alle Rto og det er også kontinuerligt der. Det følger heraf, at eksistens- og unikhedssætningen garanterer, at dette indledende værdiproblem har en unik løsning, selvom det ikke fortæller os, hvad det er..
- Eksempel 2
Overvej følgende første ordens almindelige differentialligning med starttilstand:
y '(x) = 2√y; y (0) = 0.
Er der en løsning y (x) for dette problem? I så fald skal du afgøre, om der er en eller flere end en.
Svar
Vi overvejer funktionen f (x, y) = 2√y. Funktionen F er kun defineret til y≥0, da vi ved, at et negativt tal mangler en reel rod. Hvad mere er f (x, y) er kontinuerligt i det øverste halvplan af Rto inklusive X-aksen, så eksistensen og unikheden sætning garanterer mindst en løsning i denne region.
Nu er den oprindelige betingelse x = 0, y = 0 på kanten af løsningsområdet. Derefter tager vi delafledningen af f (x, y) med hensyn til y:
.F/ ∂y = 1 / √y
I dette tilfælde er funktionen ikke defineret for y = 0, præcis hvor den oprindelige tilstand er.
Hvad fortæller sætningen os? Det fortæller os, at selvom vi ved, at der er mindst én løsning, er det øverste halvplan af X-aksen inklusive X-aksen, da unikhedsbetingelsen ikke er opfyldt, er der ingen garanti for, at der vil være en unik løsning.
Dette betyder, at der kan være en eller flere end en løsning i kontinuitetsområdet for f (x, y). Og som altid fortæller sætningen os ikke, hvad de kunne være.
Løst øvelser
- Øvelse 1
Løs Cauchy-problemet i eksempel 1:
y '(x) = - y; med y (1) = 3.
Find funktionen y (x), der opfylder differentialligningen og starttilstanden.
Opløsning
I eksempel 1 blev det bestemt, at dette problem har en løsning og også er unikt. For at finde løsningen er den første ting at bemærke, at det er en differentialligning af den første grad af adskillelige variabler, der skrives som følger:
dy / dx = - y → dy = -y dx
Opdeling mellem og i begge medlemmer for at adskille de variabler, vi har:
dy / y = - dx
Den ubestemte integral anvendes i begge medlemmer:
∫ (1 / y) dy = - ∫dx
Løsning af de ubestemte integraler, vi har:
ln (y) = -x + C
hvor C er en konstant integration, der bestemmes af den oprindelige tilstand:
ln (3) = -1 + C, det vil sige C = 1 + ln (3)
Udskiftning af værdien af C og omarrangering forbliver:
ln (y) - ln (3) = -x + 1
Anvendelse af følgende logaritmeegenskaber:
Forskellen mellem logaritmer er kvotientens logaritme
Ovenstående udtryk kan omskrives således:
ln (y / 3) = 1 - x
Den eksponentielle funktion med base e i begge medlemmer anvendes til at opnå:
y / 3 = e(1 - x)
Hvilket svarer til:
y = 3e e-x
Dette er den unikke opløsning af ligningen y '= -y med y (1) = 3. Grafen for denne opløsning er vist i figur 1.
- Øvelse 2
Find to løsninger på problemet i eksempel 2:
y '(x) = 2√ (y); y (0) = 0.
Opløsning
Det er også en ligning af adskillelige variabler, der, skrevet i differentiel form, ser sådan ud:
D y / √ (y) = 2 dx
At tage den ubestemte integral i begge medlemmer forbliver:
to √ (y) = 2 x + C.
Hvordan kan du vide, at y≥0 i løsningsområdet har vi:
y = (x + C)to
Men da den oprindelige betingelse x = 0, y = 0 skal være opfyldt, er konstanten C nul, og følgende løsning forbliver:
y (x) = xto.
Men denne løsning er ikke unik, funktionen y (x) = 0 er også en løsning på det stillede problem. Eksistens- og unikhedssætningen anvendt på dette problem i eksempel 2 havde allerede forudsagt, at der kunne være mere end en løsning.
Referencer
- Coddington, Earl A.; Levinson, Norman (1955), Theory of Ordinary Differential Equations, New York: McGraw-Hill.
- Encyklopædi for matematik. Cauchy-Lipschitz sætning. Gendannet fra: encyclopediaofmath.org
- Lindelöf, Sur l'application de la méthode des approximations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l'Académie des sciences. Bind 116, 1894, s. 454-457. Gendannet fra: gallica.bnf.fr.
- Wikipedia. Picards successive tilnærmelsesmetode. Gendannet fra: es.wikipedia.com
- Wikipedia. Picard-Lindelöf sætning. Gendannet fra: es.wikipedia.com.
- Zill, D. 1986. Elementære differentialligninger med applikationer. Læresal.



Endnu ingen kommentarer