
Horisontale skudkarakteristika, formler og ligninger, øvelser
Det vandret skud Det er lanceringen af et projektil med vandret hastighed fra en bestemt højde og tilbage til tyngdekraften. Uden at tage højde for luftmodstand vil stien, der er beskrevet af mobilen, have form som en parabelbue.
At projicere objekter vandret er ret almindeligt. Projektilerne lanceres til alle mulige formål: fra stenene, som dæmningerne blev slået med i begyndelsen af historien, til dem, der blev udført i boldsports og følges tæt af folkemængder.
Artikelindeks
- 1 Funktioner
- 2 Formler og ligninger
- 2.1 Position, hastighed, flyvetid og maksimalt vandret rækkevidde
- 3 Løst øvelser
- 3.1-Øvelse løst 1
- 3.2 -Løst øvelse 2
- 4 Referencer
Egenskaber
De vigtigste egenskaber ved det vandrette skud er:
-Projektilets starthastighed er vinkelret på tyngdekraften.
-Bevægelsen finder sted i et plan, så det tager to koordinater: x Y Y.
-Det gøres fra en bestemt højde H over jordoverfladen.
-Den tid projektilet varer i luften kaldes flyvetid.
-Faktorer som luftmodstand og udsving i værdien af g.
-Projektilets form, størrelse og masse påvirker ikke dets bevægelse.
-Bevægelsen nedbrydes i to samtidige bevægelser: en lodret nedad under handling af g; den anden, vandret, med konstant hastighed.
Formler og ligninger
De kinematiske ligninger til vandret lancering fås fra ligningerne for frit fald og dem for ensartet retlinet bevægelse..
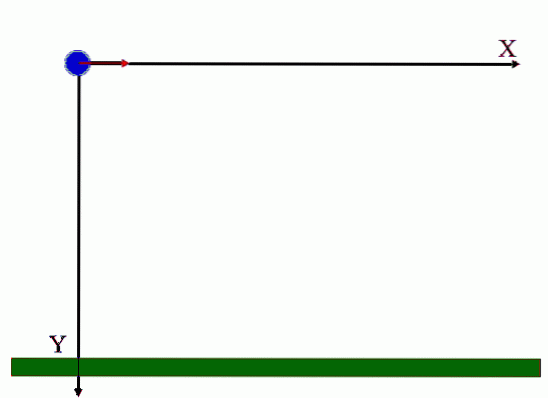
Som animationen i figur 1 tydeligt viser, får projektilet en vandret starthastighed, betegnet som veller = vokse jeg (fed i trykt tekst angiver, at det er en vektor).
Bemærk, at starthastigheden har størrelse vokse og er rettet langs aksen x, hvad er retningen af enhedsvektoren jeg. Animationen viser også, at starthastigheden ikke har en lodret komponent, men når den falder, stiger denne komponent ensartet takket være handlingen af g, tyngdekraftsacceleration.
Hvad angår den vandrette komponent af hastighed, forbliver den konstant i bevægelsens varighed.
Ifølge ovennævnte etableres positionerne som en funktion af tiden, både på den vandrette akse og på den lodrette akse. Retningen til højre tages som + x-aksen, mens retningen ned er -y-retningen. Værdien af tyngdekraften er g = -9,8 m / sto eller -32 fod / sto:
x (t) = xeller + vokse.t (vandret position); vokse det er konstant
y (t) = yeller + vHej.t - ½ g.tto (lodret position); vY = vHej - g.t (lodret hastighed)
Position, hastighed, flyvetid og maksimalt vandret rækkevidde
Ligningerne forenkles ved at vælge følgende startpositioner: xeller = 0, Yeller = 0 på lanceringsstedet. Hvad mere er vHej = 0, da mobilen projiceres vandret. Med dette valg er bevægelsesligningerne sådan:
x (t) = vokse.t; vx = vokse
y (t) = - ½ g.tto; vY = - g.t
Når tiden ikke er tilgængelig, er ligningen, der vedrører hastigheder og forskydninger, nyttig. Dette gælder for den lodrette hastighed, da den vandrette forbliver konstant under hele bevægelsen:
vYto = vHejto + 2.g .y = 2.g.y
Flyvetid
For at beregne flyvetid tflyvningen, Antag, at mobilen projiceres fra en højde H på gulvet. Da oprindelsen til referencesystemet er valgt ved startpunktet, når det når jorden, er det i position -H. Ved at erstatte dette i ligning 2) får vi:
-H = - ½ g.ttoflyvningen
tflyvningen = (2H / g)½
Maksimal rækkevidde
Det vandret rækkevidde opnås ved at erstatte denne gang i x (t):
xmaks = vokse. (2H / g)½
Løst øvelser
-Løst øvelse 1
En helikopter flyver vandret og opretholder en konstant højde på 580 m, når den smider en kasse med mad over en flygtningelejr. Kassen lander i en vandret afstand på 150 m fra startpunktet. Find: a) Kassens flyvetid.
b) Helikopterens hastighed.
c) Hvor hurtigt rørte kassen jorden??
Opløsning
a) Højden H, hvorfra maden tabes, er H = 500 m. Med disse data når vi erstatter, opnår vi:
tflyvningen = (2H / g)½= (2 x 580 / 9,8) ½s = 10,9 s
b) Helikopteren har den oprindelige vandrette hastighed vokse af pakken, og da en af dataene er xmaks:
xmaks = vokse. (2H / g)½ ® vokse = xmaks / (2H / g)½= xmaks / tflyvningen = 150 m / 10,9 s = 13,8 m / s
c) Projektilets hastighed til enhver tid er:
vY = -g.t = -9,8 m / sto x 10,9 s = -106,82 m / s = - 384,6 km / t
Det negative tegn indikerer, at mobilen bevæger sig nedad.
-Træning løst 2
Fra et fly, der flyver vandret i en højde H = 500 m Y 200 km / t en pakke falder og skal falde på et åbent køretøj, der kører ved 18 km / t på vejen. I hvilken position skal flyet tabe pakken, så den falder i køretøjet? Tag ikke højde for luftmodstand eller vindhastighed.
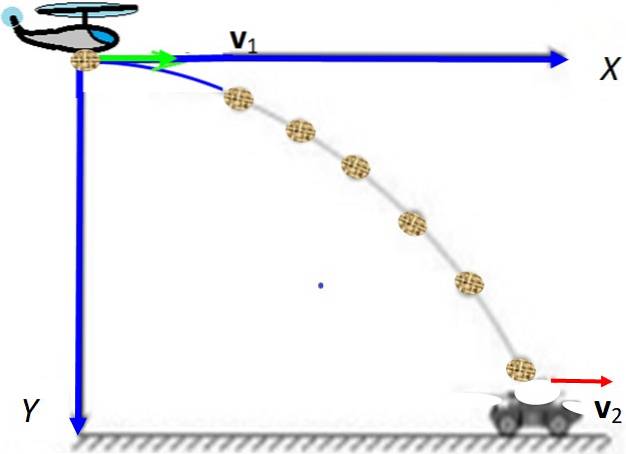
Opløsning
Det er praktisk først at overføre alle enhederne til det internationale system:
18 km / t = 6 m / s
200 km / t = 55 m / s
Der er to mobiltelefoner: fly (1) og køretøj (2), og det er nødvendigt at vælge et koordinatsystem for at lokalisere dem begge. Det er praktisk at gøre det ved startpunktet for pakken på flyet. Pakken projiceres vandret med den hastighed, som flyet bærer: v1, mens køretøjet kører på vto antages konstant.
-Fly
Udgangsposition: x = 0; y = 0
Starthastighed = v1 (vandret)
Ligninger af position: y (t) = -½g.tto ; x (t) = v1.t
-Køretøj
Udgangsposition: x = 0, y = -H
Starthastighed = vto (konstant)
x (t) = xeller + vto. t
Varigheden af pakkens flyvning er:
tflyvningen = (2H / g)½ = (2 × 500 / 9,8)½s = 10,1 s
På denne tid har pakken oplevet en vandret forskydning af:
xmaks = vokse . (2H / g)½= 55 m / s x 10,1 s = 556 m.
På denne tid har køretøjet også bevæget sig vandret:
x (t) = v1.t = 6 m / s x10,1 s = 60,6 m
Hvis flyet taber pakken med det samme, når det ser køretøjet passere under det, får det ikke det til at falde lige ned i det. For at dette skal ske, skal du smide det længere tilbage:
d = 556 m - 60,6 m = 495,4 m.
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill. 74-84.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 1. kinematik. Redigeret af Douglas Figueroa (USB). 117 - 164.
- Projektilbevægelse. Gendannet fra: phys.libretexts.org.
- Rex, A. 2011. Grundlæggende fysik. Pearson. 53-58.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. McGraw Hill. 126-131.



Endnu ingen kommentarer