
Diskrete Fourier-transformationsegenskaber, applikationer, eksempler
Det diskret Fourier-transformation er en numerisk metode, der bruges til at definere prøver, der henviser til de spektrale frekvenser, der udgør et signal. Undersøg periodiske funktioner i lukkede parametre, hvilket giver et andet diskret signal.
For at opnå den diskrete Fourier-transformation af N-punkter på et diskret signal skal følgende 2 betingelser være opfyldt på en sekvens x [n]
x [n] = 0 n < 0 ˄ n > N - 1
Hvis disse betingelser er opfyldt, kan den diskrete Fourier-transformation defineres som
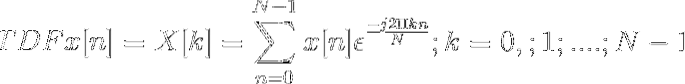
Den diskrete Fourier-transformation kan defineres som en N-punkt prøveudtagning af Fourier-transformeringen.
Artikelindeks
- 1 Fortolkning af den diskrete Fourier-transformation
- 2 egenskaber
- 2.1 Lineæritet
- 2.2 Dualitet
- 2.3 Konvolution
- 2.4 Rulning
- 2.5 Konjugatsymmetri
- 2.6 Modulation
- 2.7 Produkt
- 2.8 Symmetri
- 2.9 Konjugat
- 2.10 Parseval ligning
- 3 Ligheder og forskelle med Fourier-transformationen
- 4 Hvad er den diskrete Fourier-transformation til?
- 5 Historie
- 6 Diskret Fourier-transformation og dens inverse
- 7 vinget
- 8 applikationer
- 8.1 Beregning af den grundlæggende løsning
- 8.2 Signalteori
- 9 Fourier-serien
- 10 Andre former for Fourier-serien
- 11 Eksempler
- 12 Øvelser
- 12.1 Øvelse 1
- 12.2 Øvelse 2
- 13 Referencer
Fortolkning af den diskrete Fourier-transformation

Der er to synspunkter, hvorfra de opnåede resultater på en sekvens x kan fortolkess[n] gennem den diskrete Fourier-transformation.
-Den første svarer til de spektrale koefficienter, der allerede er kendt fra Fourier-serien. Det observeres i diskrete periodiske signaler, hvor prøver falder sammen med sekvensen xs[n].
-Den anden handler om spektret af et diskret aperiodisk signal med prøver svarende til sekvensen xs[n].
Den diskrete transformation er en tilnærmelse til spektret af det originale analoge signal. Dens fase afhænger af prøverne, mens dens størrelse afhænger af prøveintervallet..
Ejendomme
De algebraiske fundamenter af strukturen udgør de logiske baser i de følgende afsnit.
Lineæritet
C. Sn → C. F [Sk]; Hvis en sekvens ganges med en skalar, vil dens transformation også være.
Tn + Vn = F [Tk] + F [Vk]; Transformationen af en sum er lig med summen af transformationerne.
Dualitet
F [Sn] → (1 / N) S-k; Hvis den diskrete Fourier-transformation genberegnes til et allerede transformeret udtryk, opnås det samme udtryk, skaleret i N og inverteret i forhold til den lodrette akse.
Konvolution
Ved at forfølge lignende mål som i Laplace-transformen henviser sammensmeltning af funktioner til produktet mellem deres Fourier-transformationer. Konvolution gælder også for diskrete tider og er ansvarlig for mange moderne procedurer..
xn * Rn → F [Xn] .F [Rn]; Transformationen af en konvolution er lig med transformationsproduktet.
xn . Rn→ F [Xn] * F [Rn]; Transformationen af et produkt er lig med transformationen.
Forskydning
xn-m → F [Xk] e -i (2π / N) km ; Hvis en sekvens er forsinket i m-prøver, vil dens virkning på den diskrete transformation være en ændring af vinklen defineret med (2π / N) km.
Symmetri konjugeret
xt [-k] = X *t[k] = Xt [N - K]
Modulation
W-nmN . x [n] ↔ Xt[k - m]
Produkt
x [n] y [n] ↔ (1 / N) Xt[k] * Yt[k]
Symmetri
X [-n] ↔ Xt[-k] = X *t[k]
Konjugat
x * [n] ↔ X *t[-k]
Parseval ligning
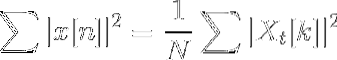
Ligheder og forskelle med Fourier-transformationen
Med hensyn til den konventionelle Fourier-transformation har den flere ligheder og forskelle. Fourier-transformeringen konverterer en sekvens til en solid linje. På denne måde siges det, at resultatet af Fourier-variablen er en kompleks funktion af en reel variabel.
Den diskrete Fourier-transformation modtager i modsætning til et diskret signal og omdanner det til et andet diskret signal, det vil sige en sekvens.
Hvad er den diskrete Fourier-transformation til?
De tjener primært til at forenkle ligninger betydeligt, samtidig med at afledte udtryk omdannes til magtelementer. Betegnelse af differentielle udtryk i form af integrerbare polynomer.
I optimering, modulering og modellering af resultater fungerer det som et standardiseret udtryk og er en hyppig ressource til teknik efter flere generationer.
Historie
Dette matematiske koncept blev præsenteret af Joseph B. Fourier i 1811, mens han udviklede en afhandling om varmespredning. Det blev hurtigt vedtaget af forskellige grene inden for videnskab og teknik.
Det blev etableret som det vigtigste arbejdsredskab i studiet af ligninger med delvise derivater, endda sammenlignet med det eksisterende arbejdsforhold mellem Laplace-transformation og almindelige differentialligninger.
Hver funktion, der kan arbejdes med en Fourier-transformation, skal præsentere null uden for en defineret parameter.
Diskret Fourier-transformation og dens inverse
Den diskrete transformation opnås gennem udtrykket:
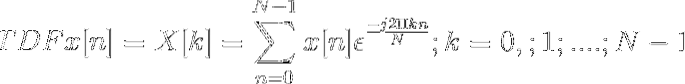
Efter at have givet en diskret sekvens X [n]
Den inverse af den diskrete Fourier-transformation er defineret gennem udtrykket:
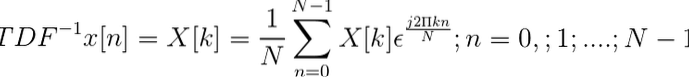
Når den diskrete transformation er opnået, tillader den at definere sekvensen i tidsdomænet X [n].
Bevinget
Parametriseringsprocessen svarende til den diskrete Fourier-transformation ligger i vinduesvinduet. For at udføre transformationen skal vi begrænse sekvensen i tid. I mange tilfælde har de pågældende signaler ikke disse begrænsninger.
En sekvens, der ikke opfylder størrelseskriterierne, der skal anvendes på den diskrete transformation, kan ganges med en "vindues" -funktion V [n], der definerer sekvensens opførsel i en kontrolleret parameter.
X [n]. V [n]
Spektrumets bredde afhænger af vinduets bredde. Når vinduets bredde øges, vil den beregnede transformation være smallere.
Ansøgninger
Beregning af den grundlæggende løsning
Den diskrete Fourier-transformation er et kraftfuldt værktøj til undersøgelse af diskrete sekvenser.
Den diskrete Fourier-transformation forvandler en kontinuerlig variabel funktion til en diskret variabel transformation.
Cauchy-problemet for varmeligningen præsenterer et hyppigt anvendelsesområde for den diskrete Fourier-transformation. Hvor funktionen genereres varmekerne eller Dirichlet-kerne, hvilket gælder for prøveudtagning af værdier i en defineret parameter.
Signal teori
Den generelle årsag til anvendelsen af den diskrete Fourier-transformation i denne gren skyldes hovedsageligt den karakteristiske nedbrydning af et signal som en uendelig superposition af lettere behandlingsbare signaler.
Det kan være en lydbølge eller en elektromagnetisk bølge, den diskrete Fourier-transformation udtrykker den i en superposition af enkle bølger. Denne repræsentation er ret hyppig inden for elektroteknik.
Fourier-serien
De er serier defineret i form af Cosines og Sines. De tjener til at lette arbejdet med generelle periodiske funktioner. Når de anvendes, er de en del af teknikkerne til løsning af almindelige og delvise differentialligninger..
Fourier-serien er endnu mere generel end Taylor-serien, fordi de udvikler periodiske diskontinuerlige funktioner, der ikke har en Taylor-serierepræsentation..
Andre former for Fourier-serien
For at forstå Fourier-transformationen analytisk er det vigtigt at gennemgå de andre måder, hvorpå Fourier-serien kan findes, indtil vi kan definere Fourier-serien i dens komplekse notation..
-Fourier-serier på en 2L periode-funktion:
Mange gange er det nødvendigt at tilpasse strukturen i en Fourier-serie til periodiske funktioner, hvis periode er p = 2L> 0 i intervallet [-L, L].
-Fourier-serier i ulige og lige funktioner
Intervallet [-π, π] betragtes, hvilket giver fordele, når man udnytter funktionernes symmetriske egenskaber.
Hvis f er jævn, etableres Fourier-serien som en serie Cosines.
Hvis f er ulige, etableres Fourier-serien som en serie af Sines.
-Kompleks notation af Fourier-serien
Hvis vi har en funktion f (t), der opfylder alle kravene i Fourier-serien, er det muligt at angive den i intervallet [-t, t] ved hjælp af dens komplekse notation:
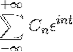
Eksempler
Med hensyn til beregningen af den grundlæggende løsning præsenteres følgende eksempler:
Laplace ligning
Varmeligning
Schrödinger ligning
Bølge ligning
På den anden side er følgende eksempler på anvendelsen af den diskrete Fourier-transformation inden for signalteori:
-Problemer med systemidentifikation. Etableret f og g
-Problem med udgangssignalkonsistens
-Problemer med signalfiltrering
Uddannelse
Øvelse 1
Beregn den diskrete Fourier-transformation for den følgende sekvens.
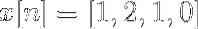
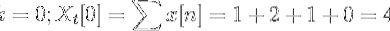
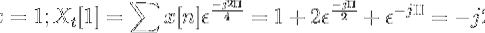
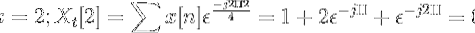
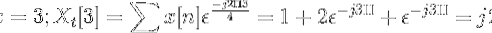
Du kan definere PTO på x [n] som:
xt[k] = 4, -j2, 0, j2 for k = 0, 1, 2, 3
Øvelse 2
Vi ønsker ved hjælp af en digital algoritme at bestemme det spektrale signal defineret af udtrykket x (t) = e-t. Hvor den maksimale frekvens, der anmoder om koefficient, er fm= 1Hz. En harmonisk svarer til f = 0,3 Hz. Fejlen er begrænset til mindre end 5%. Beregn Fs , D og N.
Under hensyntagen til prøveeksemplet Fs = 2fm = 2 Hz
En frekvensopløsning på F0 = 0,1 Hz, hvorfra du får D = 1 / 0,1 = 10s
0,3 Hz er frekvensen svarende til indekset k = 3, hvor N = 3 × 8 = 24 prøver. Angiver det Fs = N / A = 24/10 = 2,4> 2
Da målet er at få den lavest mulige værdi for N, kan følgende værdier betragtes som en løsning:
F0 = 0,3 Hz
D = 1 / 0,3 = 3,33 s
k = 1
N = 1 × 8 = 8
Referencer
- At mestre den diskrete Fourier-transformation i en, to eller flere dimensioner: faldgruber og artefakter. Isaac Amidror. Springer Science & Business Media, 19. juli. 2013
- DFT: En brugervejledning til diskret Fourier-transformation. William L. Briggs, Van Emden Henson. SIAM, 1. jan. nitten femoghalvfems
- Digital signalbehandling: Teori og praksis. D. Sundararajan. World Scientific, 2003
- Transformationer og hurtige algoritmer til signalanalyse og repræsentationer. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6. dec. 2012
- Diskrete og kontinuerlige Fourier-transformationer: Analyse, applikationer og hurtige algoritmer. Eleanor Chu. CRC Press, 19. mar. 2008


Endnu ingen kommentarer