
Ligesidede trekantkarakteristika, egenskaber, formler, areal
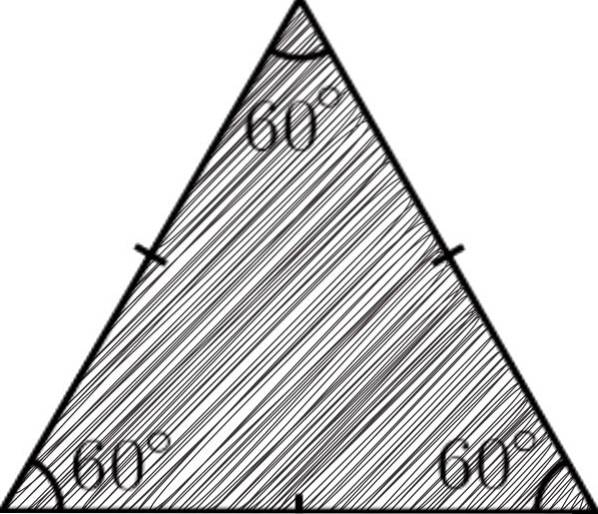
EN ligesidet trekant det er en polygon med tre sider, hvor alle er ens; det vil sige, de har samme mål. For denne egenskab fik den navnet ligesidet (lige sider).
Trekanter er polygoner, der betragtes som de enkleste i geometri, fordi de består af tre sider, tre vinkler og tre hjørner. I tilfældet med den ligesidede trekant, da den har lige sider, betyder det, at dens tre vinkler også vil være ens..
Artikelindeks
- 1 Karakteristika for ligesidede trekanter
- 1.1 - Lige sider
- 1.2 - Komponenter
- 2 egenskaber
- 2.1 Indvendige vinkler
- 2.2 Eksterne vinkler
- 2.3 Summen af siderne
- 2.4 Kongruente sider
- 2.5 Kongruente vinkler
- 3 Sådan beregnes omkredsen?
- 4 Sådan beregnes højden?
- 5 Sådan beregnes siderne?
- 6 Sådan beregnes arealet?
- 7 Øvelser
- 7.1 - Første øvelse
- 7.2 - Anden øvelse
- 7.3 - Tredje øvelse
- 8 Referencer
Karakteristika for ligesidede trekanter
- Lige sider
Ligesidede trekanter er flade og lukkede tal, der består af tre linjesegmenter. Trekanter er klassificeret efter deres egenskaber i forhold til deres sider og vinkler; den ligesidede blev klassificeret ved hjælp af målene på dens sider som en parameter, da disse er nøjagtigt de samme, det vil sige de er kongruente.
Den ligesidede trekant er et særligt tilfælde af den ligebenede trekant, fordi to af dens sider er kongruente. Derfor er alle ligesidede trekanter også ligebenede, men ikke alle ligebenede trekanter vil være ligesidede.
På denne måde har ligesidede trekanter de samme egenskaber som en ligebenet trekant..
Ligesidede trekanter kan også klassificeres efter bredden af deres indre vinkler som en ligesidet akut trekant, som har tre sider og tre indvendige vinkler med samme mål. Vinklerne vil være akutte, dvs. de vil være mindre end 90eller.
- Komponenter (rediger)
Trekanter har generelt flere linjer og punkter, der komponerer det. De bruges til at beregne arealet, siderne, vinklerne, medianen, halveringen, halveringen og højden..
- Median: er en linje, der starter fra midtpunktet på den ene side og når det modsatte toppunkt. De tre medianer konvergerer på et punkt kaldet barycenter eller centroid..
- Bisector: det er en stråle, der deler vinklerne på hjørnerne i to lige store vinkler, det er derfor, den er kendt som symmetriaksen. Den ligesidede trekant har tre akser af symmetri. I den ligesidede trekant er halveringslinjen trukket fra hjørnet af en vinkel til dens modsatte side og skærer det ved midtpunktet. Disse mødes på et punkt kaldet incenter.
- Mediatrixen: er et segment vinkelret på den side af trekanten, der har sin oprindelse i midten af det. Der er tre lægemidler i en trekant, og de mødes på et punkt kaldet circumcenter.
- Højden: er linjen, der går fra toppunktet til den side, der er modsat, og også denne linje er vinkelret på den side. Alle trekanter har tre højder, der falder sammen på et punkt kaldet ortocentret..
I den følgende graf ser vi en scalene trekant, hvor nogle af de nævnte komponenter er detaljerede
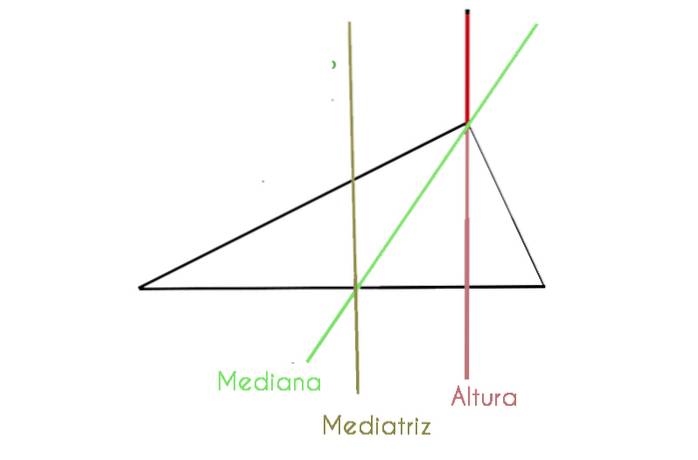
Halveringen, medianen og halveringen er sammenfaldende
Halvdelen deler siden af en trekant i to dele. I ligesidede trekanter vil den side blive opdelt i to nøjagtigt lige dele, det vil sige trekanten vil blive opdelt i to kongruente højre trekanter.
Således er halveringen trukket fra en hvilken som helst vinkel i en ligesidet trekant sammenfaldende med medianen og halveringsgraden på siden modsat denne vinkel..
Eksempel:
Den følgende figur viser trekanten ABC med et midtpunkt D, der deler en af siderne i to segment AD og BD.
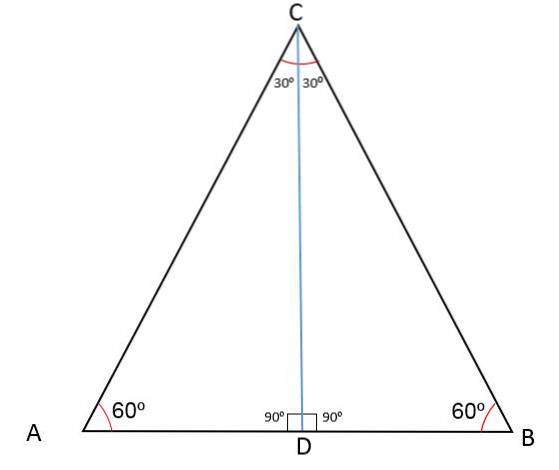
Ved at tegne en linje fra punkt D til det modsatte toppunkt opnås pr. Definition median-CD'en, som er relativ til toppunkt C og side AB.
Da segmentet CD opdeler trekanten ABC i to lige store trekanter CDB og CDA, betyder det, at kongruenssagen vil være: side, vinkel, side, og derfor vil CD også være bisector af BCD.
Plottesegment CD deler toppunktvinklen i to lige store vinkler på 30eller, vinklen på toppunkt A måler stadig 60eller og linie-CD'en danner en vinkel på 90eller med hensyn til midtpunktet D.
Segmentet CD danner vinkler, der har samme mål for trekanterne ADC og BDC, det vil sige, de er supplerende på en sådan måde, at målene for hver enkelt vil være:
Med. (ADB) + Med. (ADC) = 180eller
to * Med. (ADC) = 180eller
Med. (ADC) = 180eller ÷ 2
Med. (ADC) = 90eller.
Og så har vi, at segmentet CD også er halveringen af side AB.
Halvsnittet og højden er sammenfaldende
Ved at trække halveringen fra toppunktet i den ene vinkel til midtpunktet på den modsatte side opdeler den den ligesidede trekant i to kongruente trekanter.
På en sådan måde, at der dannes en vinkel på 90eller (ret). Dette indikerer, at linjesegmentet er helt vinkelret på den side, og pr. Definition ville linjen være højden.
På denne måde falder halveringen af en hvilken som helst vinkel i en ligesidet trekant sammen med højden i forhold til den modsatte side af denne vinkel..
Ortocenter, barycenter, incenter og sammenfaldende circumcenter
Da højden, medianen, bisektoren og den halverede del er repræsenteret af det samme segment på samme tid, i en ligesidet trekant vil mødepunkterne for disse segmenter - orthocentret, bisector, incenter og circumcenter - blive fundet på samme punkt:
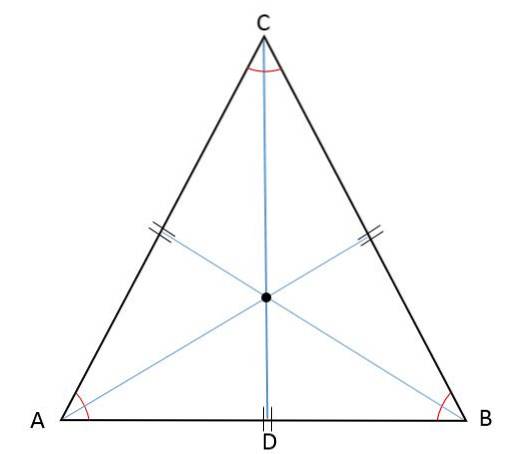
Ejendomme
Hovedegenskaben ved ligesidede trekanter er, at de altid vil være ligebenede trekanter, da ligebenede er dannet af to kongruente sider og ligesidede af tre..
På denne måde arvede de ligesidede trekanter alle egenskaberne af den ligebenede trekant:
Indvendige vinkler
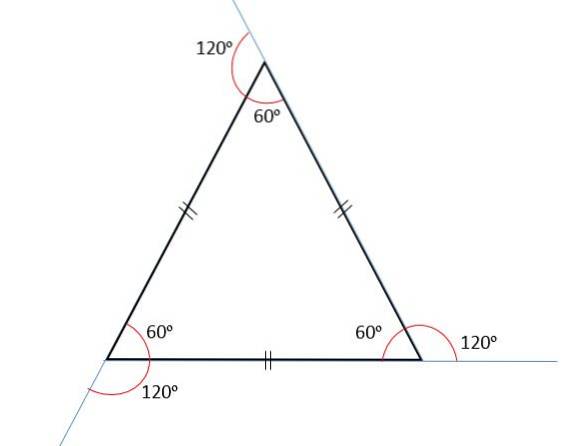
Summen af de indvendige vinkler er altid lig med 180eller, og da alle dens vinkler er kongruente, vil hver af disse måle 60eller.
Eksterne vinkler
Summen af de udvendige vinkler vil altid være 360eller, derfor måler hver udvendige vinkel 120eller. Dette skyldes, at de interne og eksterne vinkler er supplerende, dvs. når de tilføjes, vil de altid være lig med 180eller.
Summen af siderne
Summen af målene fra to sider skal altid være større end målene for den tredje side, det vil sige a + b> c, hvor a, b og c er målene for hver side.
Kongruente sider
Ligesidede trekanter har alle tre sider med samme mål eller længde; de er kongruente. Derfor har vi i det forrige punkt, at a = b = c.
Kongruente vinkler
Ligesidede trekanter er også kendt som ligekantede trekanter, fordi deres tre indvendige vinkler er kongruente med hinanden. Dette skyldes, at alle dets sider også har den samme måling.
Sådan beregnes omkredsen?
Omkredsen af en polygon beregnes ved at tilføje siderne. Som i dette tilfælde har den ligesidede trekant alle sine sider med samme mål, dens omkreds beregnes med følgende formel:
P = 3 * side.
Sådan beregnes højden?
Da højden er linjen vinkelret på basen, deler den den i to lige store dele ved at strække sig til det modsatte toppunkt. Sådan dannes to lige højre trekanter.
Højden (h) repræsenterer det modsatte ben (a), halvdelen af siden AC til det tilstødende ben (b) og siden BC repræsenterer hypotenusen (c).
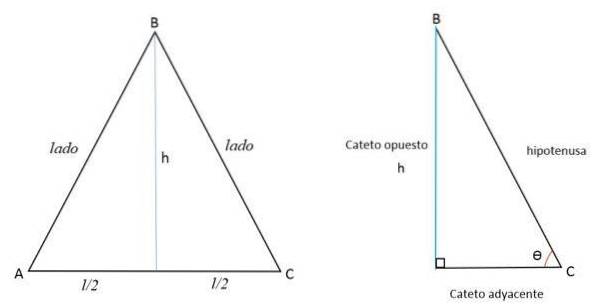
Ved hjælp af Pythagoras sætning kan værdien af højden bestemmes:
tilto + bto = cto
Hvor:
tilto = højde (h).
bto = side b / 2.
cto = side a.
Ved at erstatte disse værdier i Pythagoras sætning og løse højden har vi:
hto + ( l / to)to = lto
hto + lto/ 4 = lto
hto = lto - lto/ 4
hto = (4*lto - lto) / 4
hto = 3*lto /4
√hto = √ (3*lto /4)

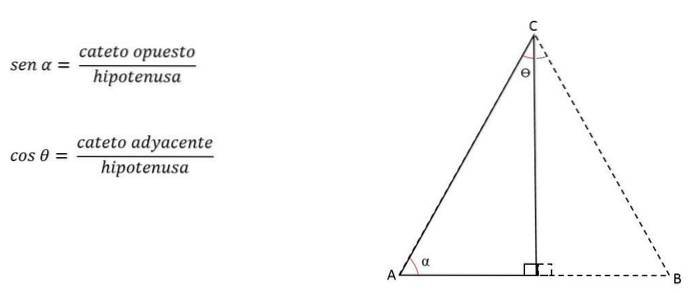
Hvis vinklen dannet af de kongruente sider er kendt, kan højden (repræsenteret af et ben) beregnes ved at anvende de trigonometriske forhold.
Benene kaldes modsatte eller tilstødende afhængigt af vinklen taget som reference..
For eksempel vil i figuren ovenfor benet h være modsat for vinkel C, men støder op til vinkel B:
Således kan højden beregnes med:
Sådan beregnes siderne?
Der er tilfælde, hvor målingerne af trekantens sider ikke er kendt, men deres højde og vinklerne dannet ved hjørnerne.
For at bestemme området i disse tilfælde er det nødvendigt at anvende de trigonometriske forhold.
Ved at kende vinklen på en af dens hjørner identificeres benene, og det tilsvarende trigonometriske forhold anvendes:
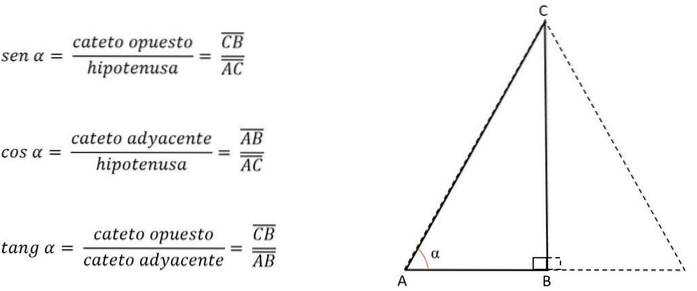
Ben AB vil således være modsat for vinkel C, men støder op til vinkel A. Afhængig af den side eller det ben, der svarer til højden, ryddes den anden side for at opnå sin værdi, idet man ved, at de tre sider altid vil have den samme måling.
Sådan beregnes arealet?
Arealet af trekanterne beregnes altid med den samme formel, gangende basis gange højden og divideres med to:
Areal = (b * h) ÷ 2
At vide, at højden er angivet med formlen:

Uddannelse
- Første øvelse
Siderne af en ligesidet trekant ABC er 20 cm hver. Beregn højden og arealet af den polygon.
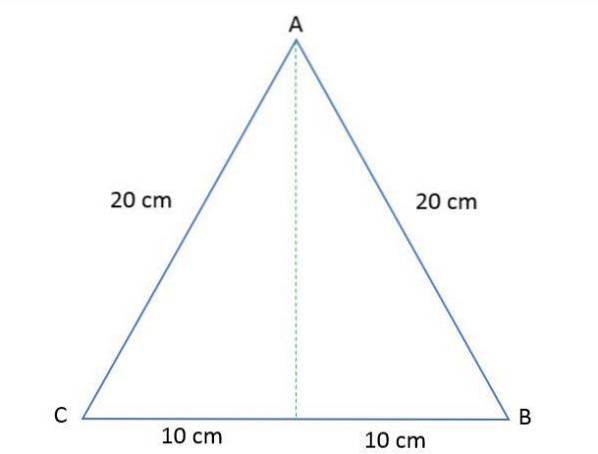
Opløsning
For at bestemme arealet af denne ligesidede trekant er det nødvendigt at beregne højden, idet man ved, at når man tegner den, deler den trekanten i to lige store trekanter.
På denne måde kan Pythagoras sætning bruges til at finde det:
tilto + bto = cto
Hvor:
a = 20/2 = 10 cm.
b = højde.
c = 20 cm.
Data er erstattet i sætningen:
10to + bto = 20to
100 cm + bto = 400 cm
bto = (400 - 100) cm
bto = 300 cm
b = √300 cm
b = 17,32 cm.
Det vil sige, at trekants højde er lig med 17,32 cm. Nu er det muligt at beregne arealet af den givne trekant ved at erstatte i formlen:
Areal = (b * h) ÷ 2
Areal = (20 cm * 17,32 cm) ÷ 2
Areal = 346,40 cmto ÷ 2
Areal = 173,20 cmto.
En anden enklere måde at løse øvelsen på er ved at erstatte dataene i den direkte formel for området, hvor værdien af højden også findes implicit:

- Anden øvelse
Blomster plantes på et stykke jord, der har form af en ligesidet trekant. Hvis landets omkreds er lig med 450 m, skal du beregne antallet af kvadratmeter, som blomsterne vil besætte.
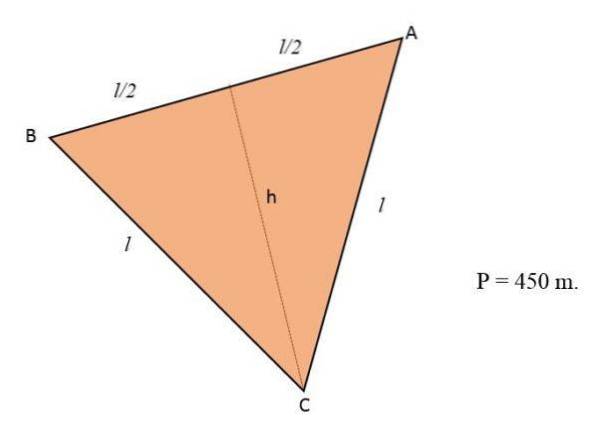
Opløsning
At vide, at omkredsen af en trekant svarer til summen af dens tre sider, og da terrænet har form af en ligesidet trekant, vil de tre sider af dette have samme mål eller længde:
P = side + side + side = 3 * l
3 * l = 450 m.
l = 450 m ÷ 3
l = 150 m.
Nu er det kun nødvendigt at beregne højden på den trekant.
Højden deler trekanten i to kongruente højre trekanter, hvor det ene ben repræsenterer højden og den anden halvdel basen. Ved den Pythagoras sætning kan højden bestemmes:
tilto + bto = cto
Hvor:
til = 150 m ÷ 2 = 75 m.
c = 150 m.
b = højde
Data er erstattet i sætningen:
(75 m)to + bto = (150 m)to
5.625 m + bto = 22.500 m
bto = 22.500 m - 5.625 m
bto = 16.875 m
b = √16,875 m
b = 129,90 m.
Således vil det område, som blomsterne besætter, være:
Areal = b * h ÷ 2
Areal = (150 m * 129,9 m) ÷ 2
Areal = (19.485 mto) ÷ 2
Areal = 9.742,5 mto
- Tredje øvelse
Den ligesidede trekant ABC er delt med et linjesegment, der går fra toppunktet C til midtpunktet D, der er placeret på den modsatte side (AB). Dette segment måler 62 meter. Beregn arealet og omkredsen af den ligesidede trekant.
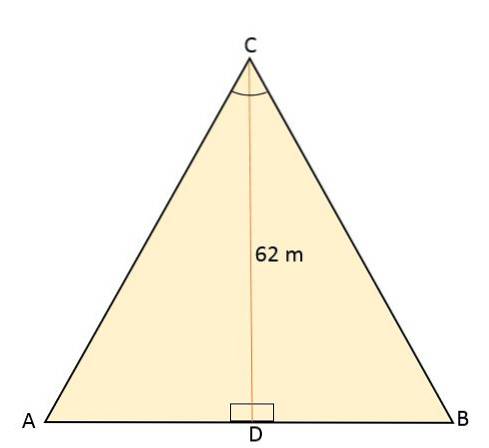
Opløsning
Ved at vide, at den ligesidede trekant er delt af et linjesegment, der svarer til højden og således danner to kongruente højre trekanter, deler dette igen også vinklen på toppunktet C i to vinkler med samme måleller hver.
Højden danner en vinkel på 90eller med hensyn til segment AB, og vinklen på toppunkt A måler derefter 60eller.
Brug derefter vinklen 30 som referenceeller, højde-CD'en er indstillet som benet ved siden af vinklen og BC som hypotenusen.
Fra disse data kan værdien af en af siderne af trekanten bestemmes ved hjælp af de trigonometriske forhold:
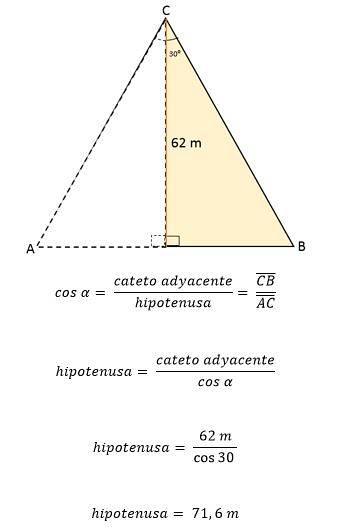
Da i den ligesidede trekant har alle sider nøjagtigt samme mål eller længde, betyder det, at hver side af den ligesidede trekant ABC er lig med 71,6 meter. Ved at vide det er det muligt at bestemme dets område:
Areal = b * h ÷ 2
Areal = (71,6 m * 62 m) ÷ 2
Areal = 4.438,6 mto ÷ 2
Areal = 2.219,3 mto
Omkredsen er givet af summen af dens tre sider:
P = side + side + side = 3 * l
P = 3*l
P = 3 * 71,6 m
P = 214,8 m.
Referencer
- Álvaro Rendón, A. R. (2004). Teknisk tegning: aktivitetsbog.
- Arthur Goodman, L. H. (1996). Algebra og trigonometri med analytisk geometri. Pearson Uddannelse.
- Baldor, A. (1941). Algebra. Havana: Kultur.
- BARBOSA, J. L. (2006). Plan euklidisk geometri. SBM. Rio de Janeiro, .
- Coxford, A. (1971). Geometri En transformationsmetode. USA: Laidlaw Brothers.
- Euclid, R. P. (1886). Euclids elementer af geometri.
- Héctor Trejo, J. S. (2006). Geometri og trigonometri.
- León Fernández, G. S. (2007). Integreret geometri. Metropolitan Technological Institute.
- Sullivan, J. (2006). Algebra og trigonometri. Pearson Uddannelse.


Endnu ingen kommentarer