Det statistiske variabler De er egenskaber, som mennesker, ting eller steder har, og som kan måles. Eksempler på hyppigt anvendte variabler er alder, vægt, højde, køn, civilstand, akademisk niveau, temperatur, antallet af timer en glødepære varer og mange andre..
Et af videnskabens mål er at vide, hvordan et systems variabler opfører sig for at forudsige dets fremtidige opførsel. I henhold til sin art kræver hver variabel en specifik behandling for at opnå den maksimale information fra den..
Antallet af variabler, der skal undersøges, er enormt, men når vi undersøger den førnævnte gruppe nøje, bemærker vi straks, at nogle kan udtrykkes numerisk, mens andre ikke kan..
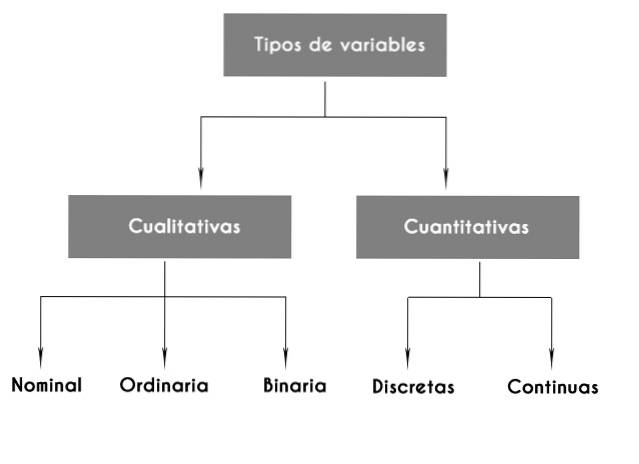
Dette giver anledning til en indledende klassificering af statistiske variabler i to grundlæggende typer: kvalitativ og numerisk..
Artikelindeks
Som navnet antyder, bruges kvalitative variabler til at betegne kategorier eller kvaliteter.
Et velkendt eksempel på denne type variabler er civilstand: enlig, gift, skilt eller enke. Ingen af disse kategorier er større end den anden, men kun en anden situation.
Flere variabler af denne type er:
-Fagligt niveau
-Måned af året
-Mærke af bil, der køres
-Erhverv
-Nationalitet
-Lande, byer, distrikter, amter og andre territoriale divisioner.
En kategori kan også betegnes med et nummer, for eksempel telefonnummer, husnummer, gade eller postnummer, uden at dette repræsenterer en numerisk vurdering, men snarere en etiket.
De kvalitative variabler kan være igen:
-Nominel, der tildeler et navn til kvaliteten, f.eks. farven.
-Ordinaler, der repræsenterer orden, som i tilfældet med en skala af socioøkonomiske lag (høj, medium, lav) eller meninger om en slags forslag (for, ligegyldig, imod). *
-Binær, ringer også dikotom, Der er kun to mulige værdier, såsom køn. Denne variabel kan tildeles en numerisk etiket, såsom 1 og 2, uden at repræsentere numerisk evaluering eller nogen form for rækkefølge.
*Nogle forfattere inkluderer ordinale variabler i gruppen af kvantitative variabler, som er beskrevet nedenfor. Det er fordi de udtrykker orden eller hierarki.
Disse variabler tildeles et nummer, da de repræsenterer mængder, såsom løn, alder, afstande og karakterer opnået i en eksamen.
De bruges i vid udstrækning til at kontrastere præferencer og estimere tendenser. Kan associeres med kvalitative variabler og oprette søjlediagrammer og histogrammer, der letter visuel analyse.
Nogle numeriske variabler kan omdannes til kvalitative variabler, men det modsatte er ikke muligt. For eksempel kan den numeriske variabel "alder" opdeles i intervaller med tildelte etiketter, såsom spædbørn, børn, unge, voksne og ældre.
Det skal dog bemærkes, at der er operationer, der kan udføres med numeriske variabler, som naturligvis ikke kan udføres med kvalitative, for eksempel beregning af gennemsnit og andre statistiske estimatorer..
Hvis du vil foretage beregninger, skal du holde variablen "alder" som en numerisk variabel. Men andre applikationer kræver muligvis ikke numeriske detaljer, for disse er det nok at efterlade de navngivne etiketter.
Numeriske variabler er igen opdelt i to store kategorier: diskrete variabler og kontinuerlige variabler..
Diskrete variabler tager kun bestemte værdier og er karakteriseret ved at kunne tælles, for eksempel antallet af børn i en familie, antallet af kæledyr, antallet af kunder, der besøger en butik dagligt, og abonnenter på et kabelfirma, for at nævne nogle eksempler.
Definere for eksempel variablen "antal kæledyr", det tager dens værdier fra sættet med naturlige tal. En person kan have 0, 1, 2, 3 eller flere kæledyr, men for eksempel aldrig 2,5 kæledyr.
Imidlertid har en diskret variabel nødvendigvis naturlige eller heltal værdier. Desimaltal er også nyttige, da kriteriet for at bestemme, om en variabel er diskret, er at den kan tælles eller tælles.
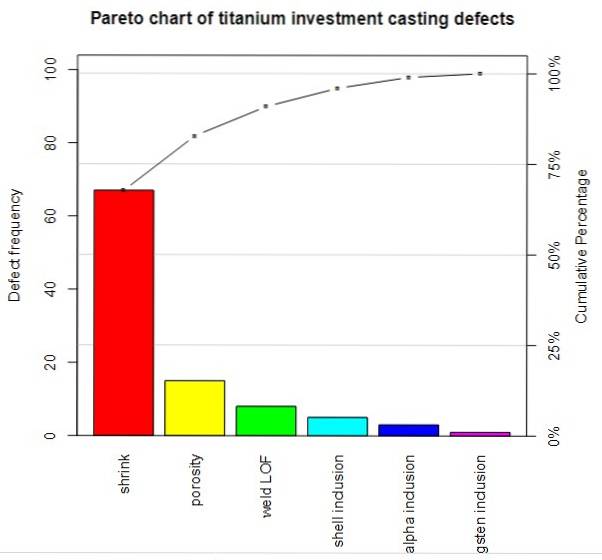
Antag for eksempel, at brøkdelen af defekte pærer i en fabrik, taget fra en stikprøve på 50, 100 eller N-pærer tilfældigt, er defineret som en variabel..
Hvis ingen pærer er defekte, tager variablen værdien 0. Men hvis 1 af N pærer er defekt, er variablen 1 / N, hvis der er to defekte, er den 2 / N og så videre indtil den begivenhed, at N pærer var defekte, og i dette tilfælde ville fraktionen være 1.
I modsætning til diskrete variabler kan kontinuerlige variabler have en hvilken som helst værdi. For eksempel vægten af studerende, der tager et bestemt emne, højde, temperatur, tid, længde og mange flere.
Da den kontinuerlige variabel tager uendelige værdier, kan alle slags beregninger foretages med den med den ønskede præcision, bare ved at justere antallet af decimaler..
I praksis er der kontinuerlige variabler, der kan udtrykkes som diskrete variabler, for eksempel en persons alder.
En persons nøjagtige alder kan tælles i år, måneder, uger, dage og mere afhængigt af den nøjagtighed, der ønskes, men den afrundes normalt i år og bliver dermed diskret.
En persons indkomst er også en kontinuerlig variabel, men det arbejdes normalt bedre, hvis der er etableret intervaller.
De afhængige variabler er de, der måles under et eksperiment for at undersøge det forhold, de har med andre, hvilket ville blive betragtet som de uafhængige variabler.
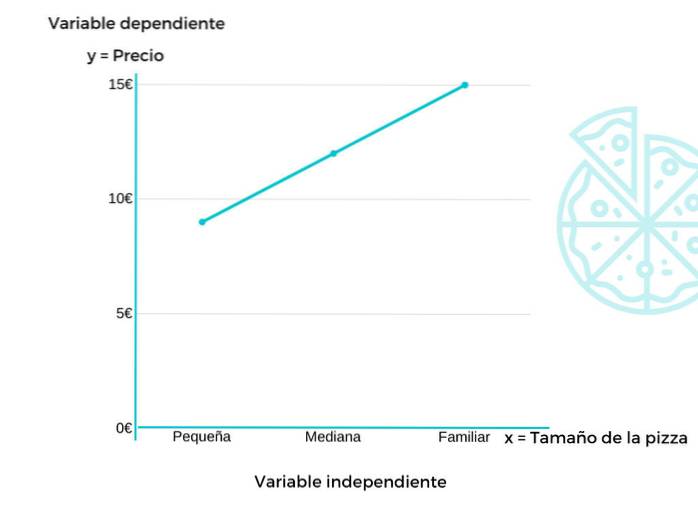
I dette eksempel vil vi se udviklingen i priser, som en fødevarevirksomheds pizzaer har lidt, afhængigt af deres størrelse.
Den afhængige variabel (y) er prisen, mens den uafhængige variabel (x) er størrelsen. I dette tilfælde koster den lille pizza € 9, den mellemste € 12 og familien en € 15.
Når pizzaens størrelse øges, koster det mere. Derfor vil prisen være afhængig af størrelsen.
Denne funktion ville være y = f (x)
Et simpelt eksempel: vi ønsker at undersøge effekten produceret af ændringer i strømmen I gennem en metaltråd, for hvilken spændingen V mellem enderne af denne ledning måles.
Den uafhængige variabel (årsagen) er strømmen, mens den afhængige variabel (effekten) er spændingen, hvis værdi afhænger af strømmen, der passerer gennem ledningen..
I eksperimentet er det, der søges, at vide, hvordan loven er for V, når jeg varieres. Hvis spændingens afhængighed med strømmen viser sig at være lineær, det vil sige: V ∝ I, lederen er ohmsk, og proportionalitetskonstanten er ledningens modstand.
Men det faktum, at en variabel er uafhængig i et eksperiment, betyder ikke, at det er sådan i et andet. Dette vil afhænge af det fænomen, der undersøges, og hvilken type forskning der skal udføres..
For eksempel bliver strømmen I, der passerer gennem en lukket leder, der roterer i et konstant magnetfelt, den afhængige variabel med hensyn til tid t, som bliver den uafhængige variabel.
Endnu ingen kommentarer