
Vektorer teamlinser definition, notation, øvelser
To eller flere vektorer er teamlinser hvis de har det samme modul, den samme retning og den samme sans, selvom deres oprindelsessted er forskelligt. Husk at egenskaberne ved en vektor er nøjagtigt: oprindelse, modul, retning og sans.
Vektorer er repræsenteret af et orienteret segment eller en pil. Figur 1 viser repræsentationen af flere vektorer i planet, hvoraf nogle er teamlinser i henhold til den oprindeligt angivne definition..
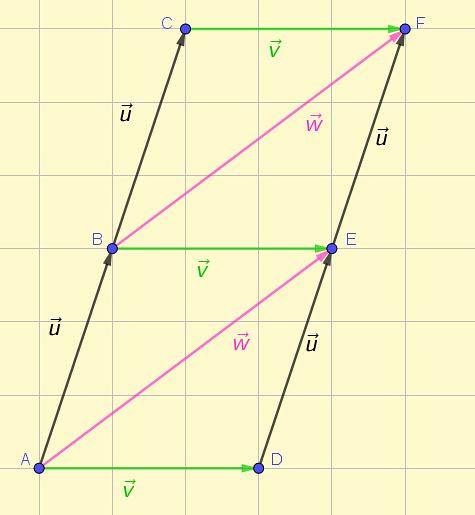
Ved første øjekast er det muligt at se, at de tre grønne vektorer har samme størrelse, samme retning og samme sans. Det samme kan siges om de to lyserøde vektorer og de fire sorte vektorer.
Mange størrelser af naturen har en vektor-lignende opførsel, sådan er tilfældet med hastighed, acceleration og kraft, for blot at nævne nogle få. Derfor er det vigtigt at karakterisere dem korrekt.
Artikelindeks
- 1 Notation for vektorer og udstyr
- 1.1 Gratis, glidende og modsatte vektorer
- 2 Øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 2.3-Øvelse 3
- 3 Referencer
Notation for vektorer og udstyr
For at skelne vektormængder fra skalære størrelser bruges ofte den fed skrift eller en pil over bogstavet. Når du arbejder med vektorer i hånden på den bærbare computer, er det nødvendigt at skelne dem med pilen, og når du bruger et trykt medium, anvendes fed skrift.
Vektorer kan betegnes ved at angive deres udgangspunkt eller oprindelsessted og deres ankomststed. For eksempel AB, F.Kr., FRA Y EF i figur 1 er vektorer i stedet for AB, F.Kr., FRA Y EF er skalære størrelser eller tal, der angiver størrelsen, modulet eller størrelsen af deres respektive vektorer.
For at indikere, at to vektorer er holdorienterede, er symbolet "∼ ". Med denne notation kan vi i figuren påpege følgende vektorer, der er holdorienterede over for hinanden:
AB∼BC∼DE∼EF
De har alle samme størrelse, retning og betydning. Derfor overholder de ovennævnte regler..
Gratis, glidende og modsatte vektorer
Enhver af vektorerne i figuren (for eksempel AB) er repræsentativt for sættet med alle faste objektiv-vektorer. Dette uendelige sæt definerer klassen af gratis vektorer eller.
eller = AB, BC, DE, EF, ...
En alternativ notation er følgende:
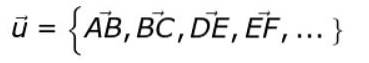
Hvis den fed eller den lille pil ikke er placeret over brevet eller, er, at vi vil henvise til vektormodulet eller.
Gratis vektorer anvendes ikke til et bestemt punkt.
For deres del glidende vektorer De er teamlængdevektorer til en given vektor, men deres anvendelsessted skal være indeholdt i handlingslinjen for den givne vektor.
Og modsatte vektorer De er vektorer, der har samme størrelse og retning, men modsatte sanser, selvom de i engelske tekster kaldes de modsatte retninger da retningen også angiver sansen. Modsatte vektorer er ikke hold.
Uddannelse
-Øvelse 1
Hvilke andre vektorer fra dem, der er vist i figur 1, er holdlinser over for hinanden??
Opløsning
Bortset fra dem, der allerede er angivet i det foregående afsnit, observeres det fra figur 1, at AD, VÆRE Y EF De er også teamlængdevektorer:
AD ∼ BE ∼ CE
Enhver af dem er repræsentativ for klassen af gratis vektorer v.
Vektorerne AE Y BF :
AE ∼ BF
Hvem er repræsentanter for klassen w.
-Øvelse 2
Punkt A, B og C er på det kartesiske plan XY og deres koordinater er:
A = (- 4.1), B = (- 1.4) og C = (- 4, -3)
Find koordinaterne for et fjerde punkt D, således at vektorerne AB Y CD være teamorienteret.
Opløsning
Så det CD være teamorienteret AB skal have det samme modul og den samme adresse som AB .
Modulet AB i kvadrat er:
|AB| ^ 2 = (-1 - (-4)) ^ 2 + (4 -1) ^ 2 = 9 + 9 = 18
Koordinaterne for D er ukendte, så vi kan sige: D = (x, y)
Derefter: |CD| ^ 2 = (x - (- 4)) ^ 2 + (y - (-3)) ^ 2
Som |AB| = |CD| er en af betingelserne for AB Y CD vær teamorienteret, du har:
(x + 4) ^ 2 + (y + 3) ^ 2 = 18
Da vi har to ukendte, kræves en anden ligning, som kan opnås ud fra den betingelse, at AB Y CD er parallelle og i samme forstand.
Hældning af vektor AB
Vektorhældningen AB angiver din adresse:
Hældning AB = (4-1) / (- 1 - (-4)) = 3/3 = 1
Angiver, at vektoren AB 45º med X-aksen.
Vector CD hældning
Hældningen af CD beregnes på samme måde:
Hældning CD = (y - (-3)) / (x - (- 4)) = (y + 3) / (x + 4)
Ligestilling af dette resultat med hældningen af AB vi har følgende ligning:
y + 3 = x + 4
Hvilket betyder, at y = x + 1.
Hvis dette resultat erstattes af ligningen af modulerne i ligningen, har vi:
(x + 4) ^ 2 + (x + 1 + 3) ^ 2 = 18
Forenkling forbliver:
2 (x + 4) ^ 2 = 18,
Hvilket svarer til:
(x + 4) ^ 2 = 9
Det vil sige x + 4 = 3, hvilket betyder, at x = -1. Så koordinaterne for D er (-1, 0).
kontrollere
Komponenterne i vektoren AB er (-1 - (- 4), 4 -1) = (3, 3)
og vektoren CD er (-1 - (- 4)); 0 - (- 3)) = (3, 3)
Hvilket betyder, at vektorerne er teamorienterede. Hvis to vektorer har de samme kartesiske komponenter, har de samme modul og retning, derfor er de teamlinser..
-Øvelse 3
Den gratis vektor eller har styrke 5 og retning 143.1301º.
Find deres kartesiske komponenter, og bestem koordinaterne for punkterne B og C, vel vidende at de faste vektorer AB og CD er holdorienterede over for dig. Koordinaterne for A er (0, 0) og koordinaterne for punkt C er (-3,2).
Opløsning
Situationen ved øvelsen kan repræsenteres ved følgende figur:
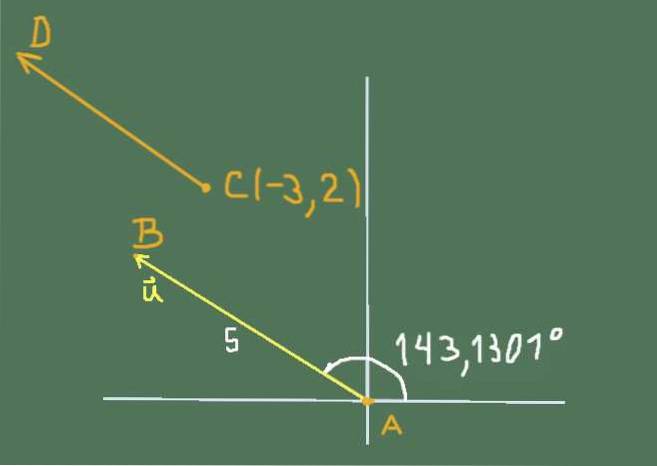
De kartesiske komponenter i eller De er
eller = (5 * cos (143.1301º); 5 * sin (143.1301º))
Udførelse af beregningerne forbliver:
eller = (-4,3)
Koordinaterne for B er ukendte, så vi placerer B (x, y)
Koordinaterne for vektoren AB er (x-0; y-0), men da u er team-linse, skal ligestillingen af komponenter være opfyldt, det følger derfor, at koordinaterne for B er (-4, 3).
Tilsvarende koordinaterne for vektoren CD er (x - (- 3)); (og - 2) at det skal være holdorienteret u, leller fører til:
x + 3 = -4 og y -2 = 3
Derefter vil koordinaterne for punkt D være (-7, 5).
Referencer
- Calculus.cc. Fast vektor. Gratis vektor. Gendannet fra: calculo.cc
- Descartes 2d. Faste vektorer og gratis flyvektorer. Gendannet fra: recursostic.educacion.es
- Guao-projekt. Vektorer holdlinser. Gendannet fra: guao.org
- Resnick, R., Krane, K. (2001). Fysik. New York: John Wiley & Sons.
- Serway, R. Jewett, John W. (2004). Fysik for forskere og ingeniører (6. udgave). Brooks / Cole.
- Tipler, Paul A. (2000). Fysik til videnskab og teknologi. Bind I. Barcelona: Ed. Reverté.
- Weisstein, E. "Vector." I Weisstein, Eric W. MathWorld. Wolfram Research.



Endnu ingen kommentarer