
Formler for gennemsnitshastighed, hvordan det beregnes og træning løses
Det gennemsnitshastighed for en mobil partikel defineres det som forholdet mellem variationen i den position, den oplever, og det tidsinterval, der anvendes i ændringen. Den enkleste situation er en, hvor partiklen bevæger sig langs en lige linje repræsenteret af x-aksen..
Antag at det bevægelige objekt indtager positioner x1 og xto i tider t1 og digto henholdsvis. Definitionen af gennemsnitshastighed vm repræsenteres matematisk sådan:

Enhederne i vm i det internationale system er de meter / sekund (m / s). Andre almindeligt anvendte enheder, der vises i tekster og mobile enheder, er: km / h, cm / s, miles / h, fødder / s og mere, så længe de er af formens længde / tid.
Det græske bogstav "Δ" læses "delta" og bruges til kort at angive forskellen mellem to størrelser..
Artikelindeks
- 1 Karakteristika for middelhastighedsvektoren vm
- 2 Tegnene på gennemsnitshastighed
- 3 Gennemsnitlig hastighed: en skalar mængde
- 4 Øvelse løst
- 5 Referencer
Karakteristika for den gennemsnitlige hastighedsvektor vm

Gennemsnitlig hastighed er en vektor, da den er relateret til ændringen i position, som igen er kendt som rulle vektor.
Denne kvalitet er gengivet med fed eller med en pil over det bogstav, der angiver størrelsen. I en dimension er den eneste mulige retning imidlertid for x-aksen, og derfor kan vektornotationen undlades.
Da vektorer har størrelse, retning og sans, indikerer et indledende kig på ligningen, at gennemsnitshastigheden vil have samme retning og følelse som forskydningen..
Forestil dig, at partiklen i eksemplet bevæger sig langs en lige linje. For at beskrive dens bevægelse er det nødvendigt at angive et referencepunkt, som vil være "oprindelsen" og betegnes som O.
Partiklen kan bevæge sig mod eller væk fra O, enten til venstre eller til højre. Det kan også tage lang eller kort tid at komme til en bestemt position..
De størrelser, der er nævnt: position, forskydning, tidsinterval og gennemsnitshastighed, beskriver partikelens opførsel, mens den bevæger sig. Det handler om størrelsesorden kinematik.
For at skelne mellem positioner eller placeringer til venstre for O bruges tegnet (-), og de til højre for O bærer tegnet (+).
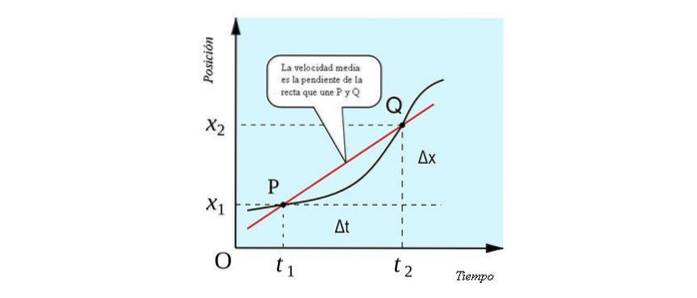
Den gennemsnitlige hastighed har en geometrisk fortolkning, der kan ses i den følgende figur. Det er linjens hældning, der passerer gennem punkterne P og Q. Når man skærer kurvepositionen vs. tid på to punkter, er det en lige linje tørring.
Tegnene på gennemsnitshastighed
Ved den følgende analyse skal det tages i betragtning tto > t1. Det vil sige, det næste øjeblik er altid større end det nuværende. På denne måde tto - t1 er altid positiv, hvilket normalt giver mening hver dag.
Derefter bestemmes tegnet på den gennemsnitlige hastighed af tegnet på xto - x1. Bemærk, at det er vigtigt at være klar over, hvor punktet O-oprindelsen er, da dette er det punkt, i forhold til hvilket partiklen siges at gå "til højre" eller "til venstre".
Enten "fremad" eller "bagud", som læseren foretrækker.
Hvis gennemsnitshastigheden er positiv, betyder det gennemsnitlig værdien af "x”Stiger med tiden, selvom det ikke betyder, at det kan være faldet på et eller andet tidspunkt i den betragtede periode. - At -.
Men globalt set i slutningen af tiden At, hun endte med en større stilling end hun havde i starten. Detaljerne i bevægelsen ignoreres i denne analyse..
Hvad hvis den gennemsnitlige hastighed viser sig at være negativ? Derefter betyder det, at partiklen slutter med en mindre koordinat end den, den startede med. Groft flyttede han tilbage. Lad os se på nogle numeriske eksempler:
Eksempel 1: Angivet start- og slutposition, angive gennemsnittets hastighedstegn. Hvor bevægede partiklen sig globalt??
a) x1 = 3 m; xto = 8 m
Svar: xto- x1 = 8 m - 3 m = 5 m. Positiv middelhastighed, partikel bevæget fremad.
b) x1 = 2 m; xto = -3 m
Svar: xto - x1 = -3 m - 2 m = -5 m. Negativ middelhastighed, partiklen bevægede sig baglæns.
c) x1 = - 5 m; xto = -12 m
Svar: xto - x1 = -12 m - (-5 m) = -7 m. Negativ middelhastighed, partiklen bevægede sig bagud.
d) x1 = - 4 m; xto = 10 m
Svar: xto - x1 = 10 m - (-4m) = 14 m. Positiv middelhastighed, partikel bevæget fremad.
Kan gennemsnitshastigheden være 0? Ja, så længe startpunktet og ankomstpunktet er det samme. Betyder dette, at partiklen nødvendigvis var i ro hele tiden??
Nej, det betyder bare, at turen var retur. Måske rejste det hurtigt eller måske meget langsomt. Indtil videre er det ikke kendt.
Gennemsnitlig hastighed: en skalar mængde
Dette får os til at definere et nyt udtryk: medium hastighed. I fysik er det vigtigt at skelne mellem vektormængder og ikke-vektormængder: skalarer.
For partiklen, der foretog rundtur, er gennemsnitshastigheden 0, men det har måske eller måske ikke været meget hurtig. For at finde ud af er gennemsnitshastigheden defineret som:

Enhederne for gennemsnitshastighed er de samme som dem for gennemsnitshastighed. Den grundlæggende forskel mellem begge størrelser er, at gennemsnitshastigheden inkluderer interessant information om retning og følelse af partiklen..
På den anden side giver gennemsnitshastigheden kun numeriske oplysninger. Med det er det kendt, hvor hurtigt eller langsomt partiklen bevægede sig, men ikke hvis den bevægede sig frem eller tilbage. Så det er en skalar størrelse. Hvordan skelner man dem, når man betegner dem? En måde er at lade fed skrift være til vektorerne eller ved at placere en pil på dem.
Og det er vigtigt at bemærke, at gennemsnitshastigheden ikke behøver at være lig med gennemsnitshastigheden. For rundtur er gennemsnitshastigheden nul, men gennemsnitshastigheden ikke. Begge har samme numeriske værdi, når de altid kører i samme retning.
Træning løst
Du kører afslappet hjem fra skolen i 95 km / t i 130 km. Det begynder at regne og sænkes ned til 65 km / t. Han kommer endelig hjem efter at have kørt i 3 timer og 20 minutter.
a) Hvor langt er dit hjem fra skolen?
b) Hvad var gennemsnitshastigheden?
Svar:
a) Nogle indledende beregninger er nødvendige:
Turen er opdelt i to dele, den samlede afstand er:
d = d1 + dto, med d1 = 130 km


t2 = 3,33 - 1,37 timer = 1,96 timer
Beregning af dto:
dto = 65 km / t x 1,96 h = 125,4 km.
Skolen er fjernt d1 + dto = 255,4 km hjemmefra.
b) Nu kan vi finde gennemsnitshastigheden:


Referencer
- Giancoli, D. Fysik. Principper med applikationer. Sjette udgave. Prentice Hall. 21-22.
- Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 20-21.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7mor. Udgave. Mexico. Cengage Learning Editors. 21-23.



Endnu ingen kommentarer