Det multiplikative problemer De undervises til børn i grundskolen efter at have lært fakta om addition og subtraktion, også kaldet addition og subtraktion..
Det er vigtigt at lære børn, at multiplikation af heltal virkelig er en sum, men det er vigtigt at lære at formere sig for at gøre disse tilføjelser hurtigere og lettere.
Det er vigtigt at vælge de første problemer, der skal bruges til at lære børn at formere sig godt, da de skal være problemer, som de kan forstå og kan se nytten af at lære at formere sig..
Det er ikke nok bare at lære dem multiplikationstabellerne mekanisk, det er meget mere attraktivt at vise dem deres brug gennem situationer, der opstår i hverdagen, som når deres forældre handler.
Der er mange problemer, der kan bruges til at lære et barn at anvende multiplikationstabeller. Nedenfor er nogle problemer med deres løsninger.
En bibliotekar skal sortere bøgerne i bibliotekshylderne. I slutningen af fredag eftermiddag indser bibliotekaren, at han stadig har brug for at bestille 78 kasser med bøger, der hver har 5 bøger. Hvor mange bøger skal bibliotekaren bestille i næste uge?
Opløsning: I dette problem skal det bemærkes, at alle felter har det samme antal bøger. Derfor repræsenterer 1 kasse 5 bøger, 2 kasser repræsenterer 5 + 5 = 10 bøger, 3 kasser repræsenterer 5 + 5 + 5 = 15 bøger. Men at gøre alle disse summer er en meget omfattende proces.
Udførelse af alle ovenstående summer svarer til at multiplicere antallet af bøger i hver kasse med antallet af resterende kasser til ordre. Nemlig, 5 × 78, derfor har bibliotekaren brug for at bestille 390 bøger.
En landmand har brug for at pakke den kaffe, der blev opnået i sin sidste høst, i kasser. Den samlede høst er 20.000 kilo, og de kasser, hvor du skal pakke dem, har en maksimal kapacitet på 100 kilo. Hvor mange kasser har landmanden brug for for at pakke hele høsten?
Opløsning: Den første ting at bemærke er, at alle kasser har samme kapacitet (100 kg). Så hvis landmanden bruger 2 kasser, kan han kun pakke 100 + 100 = 200 kg. Hvis du bruger 4 kasser, pakker du 200 + 200 = 400 kilo.
Som før er det en meget lang proces at gøre al denne mængde tilsætning. Nøglen er at finde et tal, der når det ganges med 100, er resultatet 20.000.
Ved at undersøge i detaljer kan det ses, at dette tal er 200, da 200 × 100 = 20.000.
Derfor har landmanden brug for 200 kasser til at pakke hele høsten..
Maria flyttede lige ind i en bygning og vil gerne vide, hvor mange vinduer bygningen har foran. Bygningen har 13 etager og på hver etage er der 3 vinduer.
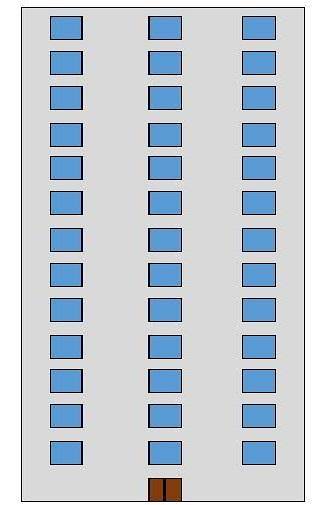
Opløsning: i dette problem kan du tælle antallet af vinduer etage for etage og tilføje dem for at få svaret.
Men da hver etage har det samme antal vinduer, er det meget hurtigere at gange antallet af etager med antallet af vinduer på hver etage. Det vil sige 13 × 3, derfor har bygningen 39 vinduer.
Javier er en murer, der bygger et badeværelsesgulv. Indtil videre har Javier placeret 9 fliser (firkanter) på badeværelsesgulvet som vist i nedenstående figur. Hvor mange fliser skal der til for at dække hele badeværelsesgulvet?
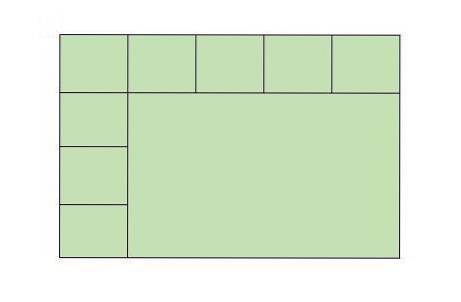
Opløsning- En måde at løse dette problem på er at udfylde figuren ved at tegne de manglende fliser og derefter tælle dem.
Men ifølge billedet kan badeværelsesgulvet passe 5 fliser vandret og 4 lodret. Derfor vil hele badeværelsesgulvet have i alt 5 × 4 = 20 fliser.
Månederne januar, marts, maj, juli, august, oktober og december har hver 31 dage. Hvad er det samlede antal dage, som alle disse måneder udgør??
Opløsning: i denne øvelse angives data eksplicit, hvilket er antallet af dage (31). De andet data gives implicit i måneder (7). Derfor er de samlede dage mellem alle disse måneder 7 × 31 = 217.
Endnu ingen kommentarer