
Absorbans hvad er det, eksempler og løste øvelser
Det absorbans er logaritmen med et negativt tegn på kvotienten mellem den fremkomne lysintensitet og den indfaldende lysintensitet på en prøve af gennemskinnelig opløsning, der er blevet belyst med monokromatisk lys. Dette kvotient er transmission.
Den fysiske proces med passage af lys gennem en prøve kaldes lystransmission, og absorbansen er et mål for den. Derfor bliver absorbansen den mindste logaritme for transmittansen og er vigtige data til bestemmelse af koncentrationen af en prøve, der generelt opløses i et opløsningsmiddel, såsom vand, alkohol eller en hvilken som helst anden..
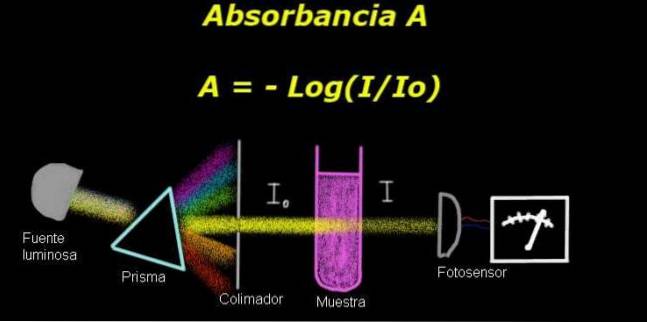
For at måle absorbans skal du bruge en enhed, der kaldes elektrofotometer, med hvilken en strøm, der er proportional med den indfaldende lysintensitet på dens overflade, måles.
Ved beregning af transmittans måles normalt intensitetssignalet svarende til opløsningsmidlet alene først, og dette resultat registreres som Io.
Derefter anbringes den opløste prøve i opløsningsmidlet under de samme lysforhold. Signalet målt af elektrofotometeret betegnes som jeg, som gør det muligt at beregne transmittansen T ifølge følgende formel:
T = I / Ieller
Det er en dimensionsløs størrelse. Det absorbans A udtrykkes således som:
A = - log (T) = - log (I / Ieller)
Artikelindeks
- 1 Molær absorbans og absorptivitet
- 1.1 Beer-Lamberts lov
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 4 Referencer
Molær absorbans og absorptivitet
Molekylerne, der udgør et kemisk stof, er i stand til at absorbere lys, og et mål for dette er netop absorbans. Det er resultatet af interaktionen mellem fotoner og molekylære elektroner.
Derfor er det en størrelsesorden, der vil afhænge af densiteten eller koncentrationen af de molekyler, der udgør prøven, og også af den optiske sti eller afstand, som lyset har kørt..
De eksperimentelle data indikerer, at absorbansen TIL er lineært proportional med koncentrationen C og på afstand d krydset af lys. Så for at beregne det baseret på disse parametre kan følgende formel etableres:
A = ε⋅C⋅d
I ovenstående formel, ε er en konstant af proportionalitet kendt som molær absorptionsevne.
Molær absorptivitet afhænger af typen af stof og den bølgelængde, hvormed absorbansen måles. Det molær absorptionsevne det er også følsomt over for prøvetemperatur og prøve pH.
Beer-Lambert Law
Dette forhold mellem absorbans, absorptionsevne, koncentration og afstand af tykkelsen på den vej, som lyset følger inden for prøven, er kendt som Beer-Lambert-loven..

Her er nogle eksempler på, hvordan du bruger det.
Eksempler
Eksempel 1
Under et eksperiment belyses en prøve med rødt lys fra en helium-neon-laser, hvis bølgelængde er 633 nm. Et elektro-fotometer måler 30 mV, når laserlys rammer direkte og 10 mV, når det passerer gennem en prøve..
I dette tilfælde er transmissionen:
T = I / Io = 10 mV / 30 mV = ⅓.
Og absorbansen er:
A = - log (⅓) = log (3) = 0,48
Eksempel 2
Hvis det samme stof placeres i en beholder, der er halvdelen af tykkelsen af den, der er anvendt i eksempel 1, skal du angive, hvor meget elektrofotometeret vil markere, når lyset fra heliumneonlaseren føres gennem prøven.
Det skal overvejes, at hvis tykkelsen falder med halvdelen, så absorberes absorbansen, der er proportional med den optiske tykkelse, med halvdelen, det vil sige A = 0,28. Transmissionen T gives af følgende forhold:
T = 10-A = 10 ^ (- 0,28) = 0,53
Elektrofotometeret læser 0,53 * 30 mV = 15,74 mV.
Løst øvelser
Øvelse 1
Vi ønsker at bestemme molær absorptionsevne for en bestemt proprietær forbindelse, der er i opløsning. For at gøre dette belyses opløsningen med lys fra en 589 nm natriumlampe. Prøven placeres i en 1,50 cm tyk prøveholder.
Udgangspunktet er en opløsning med en koncentration på 4,00 × 10 ^ -4 mol pr. Liter, og transmittansen måles, hvilket resulterer i 0,06. Brug disse data til at bestemme molens absorptionsevne for prøven..
Opløsning
For det første bestemmes absorbansen, der er defineret som den mindste logaritme til at basere ti af transmittansen:
A = - log (T)
A = - log (0,06) = 1,22
Derefter anvendes Lambert-Beer-loven, der etablerer et forhold mellem absorbans, molabsorption, koncentration og optisk længde:
A = ε⋅C⋅d
Løsning for molær absorptionsevne opnås følgende forhold:
e = A / (Cdd)
erstatter de givne værdier, vi har:
ε = 1,22 / (4,00 × 10 ^ -4 M1,5 cm) = 2030 (M⋅cm) ^ - 1
Ovenstående resultat er afrundet til tre signifikante cifre.
Øvelse 2
For at forbedre præcisionen og bestemme fejlen ved målingen af prøvenes molære absorptionsevne i øvelse 1 fortyndes prøven successivt til halvdelen af koncentrationen, og transmittansen måles i hvert tilfælde..
Fra Co = 4 × 10 ^ -4 M med transmittans T = 0,06 opnås følgende sekvens af data for transmission og absorbans beregnet ud fra transmission:
Co / 1-> 0,06-> 1,22
Co / 2-> 0,25-> 0,60
Co / 4-> 0,50-> 0,30
Co / 8-> 0.71-> 0.15
Co / 16-> 0,83-> 0,08
Co / 32-> 0,93-> 0,03
Co / 64-> 0,95-> 0,02
Co / 128-> 0,98-> 0,01
Co / 256-> 0,99-> 0,00
Udfør med disse data:
a) En graf over absorbans versus koncentration.
b) En lineær tilpasning af dataene og find hældningen.
c) Fra den opnåede hældning beregnes molær absorptionsevne.
Opløsning
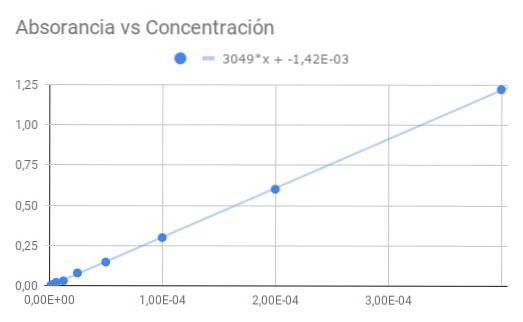
Den opnåede hældning er produktet af den molære absorberingsevne og den optiske afstand, så ved at dividere hældningen med længden 1,5 cm opnår vi den molære absorptionsevne
ε = 3049 / 1,50 = 2033 (M⋅cm) ^ - 1
Øvelse 3
Med data fra øvelse 2:
a) Beregn absorptionsevnen for hver data.
b) Bestem en gennemsnitsværdi for molær absorptionsevne, dens standardafvigelse og den statistiske fejl, der er knyttet til gennemsnittet..
Opløsning
Den molære absorptionsevne beregnes for hver af de testede koncentrationer. Husk, at lysforholdene og den optiske afstand forbliver faste.
Resultaterne for molær absorptionsevne er:
2033, 2007, 2007, 1983, 2158, 1681, 2376, 1.872, 1862 i enheder på 1 / (M * cm).
Fra disse resultater kan vi tage den gennemsnitlige værdi:
<ε> = 1998 (M * cm) ^ - 1
Med en standardafvigelse på: 184 (M * cm) ^ - 1
Den gennemsnitlige fejl er standardafvigelsen divideret med kvadratroden af antallet af data, det vil sige:
Δ<ε>= 184/9 ^ 0,5 = 60 (M * cm) ^ - 1
Endelig konkluderes det, at det patenterede stof har en molær absorptionsevne ved frekvensen 589 nm produceret af en natriumlampe på:
<ε> = (2000 ± 60) (M * cm) ^ - 1
Referencer
- Atkins, s. 1999. Fysisk kemi. Omega-udgaver. 460-462.
- Guiden. Transmittans og absorbans. Gendannet fra: quimica.laguia2000.com
- Miljøtoksikologi. Transmittans, absorbans og Lamberts lov. Gendannet fra: repositorio.innovacionumh.es
- Fysisk eventyr. Absorbans og transmission. Gendannet fra: rpfisica.blogspot.com
- Spektrofotometri. Gendannet fra: chem.libretexts.org
- Miljøtoksikologi. Transmission, absorbans og Lamberts lov. Gendannet fra: repositorio.innovacionumh.es
- Wikipedia. Absorbans Gendannet fra: wikipedia.com
- Wikipedia. Spektrofotometri. Gendannet fra: wikipedia.com


Endnu ingen kommentarer