Gennemsnitlig acceleration, hvordan det beregnes og øvelser løses

Det gennemsnitlig acceleration til_m Det er størrelsen, der beskriver variationen i en partikels hastighed i løbet af tiden. Det er vigtigt, fordi det viser de variationer, som bevægelsen oplever.

For at udtrykke denne størrelse i matematiske termer er det nødvendigt at overveje to hastigheder og to tidspunkter, der henholdsvis betegnes som v₁ og V_to, og dig₁ og dig_to.

Ved at kombinere værdierne i henhold til den tilbudte definition opnås følgende udtryk:

I det internationale SI-system er enhederne til en_m vil være m / s^to, selvom andre enheder, der involverer længde pr. tidsenhed i kvadrat, vil gøre.

For eksempel er der km / h.s, der læses "kilometer i timen og i sekundet". Bemærk, at tidsenheden vises to gange. Når man tænker på en mobil, der bevæger sig langs en lige linje, betyder det, at for hvert forløbet sekund øger mobilen sin hastighed med 1 km / t. Enten mindsker den den med 1 km / t for hvert sekund, der passerer.

Artikelindeks

• 1 Acceleration, hastighed og hastighed
• 2 Hvordan gennemsnitlig acceleration beregnes
• 3 tegn på acceleration i en-dimensionel bevægelse
• 4 Frit fald: en bevægelse med konstant acceleration
• 5 Øvelse løst
  • 5.1 Svar
• 6 Referencer

Acceleration, hastighed og hastighed

Selvom acceleration er forbundet med en stigning i hastighed, er sandheden, at nøje overholdelse af definitionen viser sig, at enhver hastighedsændring indebærer eksistensen af ​​en acceleration.

Og hastighed ændres ikke nødvendigvis altid i størrelsesorden. Det kan ske, at mobilen kun skifter retning og holder sin hastighed konstant. Der er stadig en ansvarlig acceleration af denne ændring.

Et eksempel på dette er en bil, der laver en kurve med en konstant hastighed på 60 km / t. Køretøjet udsættes for acceleration, som er ansvarlig for at ændre hastighedsretningen, så bilen følger kurven. Føreren anvender det ved hjælp af rattet.

En sådan acceleration er rettet mod midten af ​​den buede sti for at forhindre, at bilen går ud af den. Det modtager navnet på acceleration radial eller normal. Hvis den radiale acceleration pludselig blev annulleret, ville bilen ikke længere være i stand til at fortsætte rundt om kurven og ville fortsætte i en lige linje.

En bil, der kører rundt i en kurve, er et eksempel på bevægelse i to dimensioner, mens når den kører i en lige linje, er dens bevægelse endimensionel. I dette tilfælde er accelerationens eneste effekt at ændre bilens hastighed..

Denne acceleration kaldes acceleration tangentiel. Det er ikke eksklusivt for endimensionel bevægelse. Bilen, der går rundt på kurven ved 60 km / t, kan samtidig accelerere til 70 km / t, mens den tager den. I dette tilfælde skal føreren bruge både rattet og speederen..

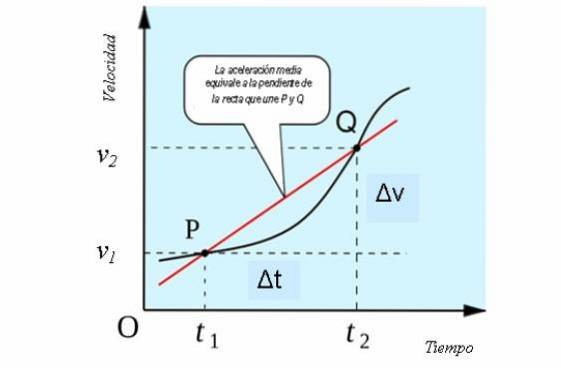
Hvis vi betragter en endimensionel bevægelse, har middelaccelerationen en geometrisk fortolkning svarende til gennemsnittets hastighed som hældningen af ​​den sekantlinie, der skærer kurven ved punkterne P og Q for hastigheden versus tidsgrafen..

Dette kan ses i følgende figur:

Hvordan beregnes gennemsnitlig acceleration

Lad os se på nogle eksempler for at beregne den gennemsnitlige acceleration i forskellige situationer:

I) På et bestemt tidspunkt har en mobil, der bevæger sig langs en lige linje, en hastighed på + 25 km / t og 120 sekunder senere har den en anden på -10 km / t. Hvad var den gennemsnitlige acceleration?

Svar

Da bevægelsen er endimensionel, kan vektornotationen udelades, i hvilket tilfælde:

v_eller = +25 km / t = +6,94 m / s

v_F = -10 km / t = - 2,78 m / s

Δt = 120 s

Når du har en øvelse med blandede størrelser som denne, hvor der er timer og sekunder, er det nødvendigt at videregive alle værdier til de samme enheder.

At være en endimensionel bevægelse, er vektornotationen udeladt.

II) En cyklist kører mod øst med en hastighed på 2,6 m / s og går 5 minutter senere mod syd med 1,8 m / s. Find dens gennemsnitlige acceleration.

Svar

Bevægelsen ikke den er endimensionel, derfor bruges vektornotationen. Enhedsvektorerne jeg Y j anvis retningerne sammen med følgende tegnkonvention, hvilket letter beregningen:

• Nord: +j
• Syd: -j
• Øst: +jeg
• Vest: -jeg

v_to = - 1,8 j Frk

v₁ = + 2,6 jeg Frk

Δt = 5 minutter = 300 sekunder

Tegn på acceleration i en-dimensionel bevægelse

Som altid med gennemsnitlige eller gennemsnitlige størrelser er de leverede oplysninger globale. De tilbyder ikke detaljer om, hvad der skete med mobilen på hvert øjeblik, men hvad de bidrager med er stadig værdifuldt til beskrivelsen af ​​bevægelsen.

Ved hjælp af tegn på både hastighed og acceleration er det muligt at vide, om en mobil, der bevæger sig på en lige linje, accelererer eller sænker farten. I begge situationer er accelerationen til stede, da hastigheden ændrer sig.

Her er nogle interessante overvejelser vedrørende tegnene på disse to størrelser:

• Gennemsnitlig hastighed og acceleration, begge med samme tegn, betyder, at set globalt går mobilen hurtigere og hurtigere.
• Hastighed og acceleration med forskellige skilte er et tegn på en mobil, der har været ret bremsende.

Det menes normalt, at når det er en negativ acceleration, bremser mobilen. Dette gælder, hvis mobilens hastighed er positiv. Men hvis det er negativt, øges hastigheden faktisk.

Som altid når du studerer bevægelse, tænk på specielle tilfælde. Hvad sker der for eksempel, når den gennemsnitlige acceleration er nul? Betyder det, at mobilen altid har holdt sin hastighed konstant??

Svaret er nej. Mobilen kunne have varieret sin hastighed i det betragtede interval, men de indledende og endelige hastigheder var de samme. I øjeblikket er detaljerne om, hvad der skete i intervallet ukendt, da den gennemsnitlige acceleration ikke giver mere information.

Hvad hvis den gennemsnitlige acceleration til_m svarer til acceleration til når som helst i tidsintervallet? Dette er en meget interessant situation kaldet Uniformly Varied Rectilinear Motion eller kort sagt MRUV..

Det betyder, at hastigheden ændres ensartet over tid. Derfor er accelerationen konstant. I naturen er der en sådan bevægelse, som alle er fortrolige med: frit fald.

Frit fald: en bevægelse med konstant acceleration

Det er en kendt kendsgerning, at jorden tiltrækker genstande mod dets centrum, og at når man frigøres i en bestemt højde, oplever den tyngdeacceleration, hvis værdi er omtrent konstant og lig med 9,8 m / s^to tæt på overfladen.

Hvis luftmodstand ikke griber ind, er bevægelsen lodret og er kendt som frit fald. Når accelerationen er konstant og vælger t₀ = 0, ligningen for den gennemsnitlige acceleration bliver:

v_F = v₀ + ved = gt (v₀= 0)

Hvor a = g = 9,8 m / s^to

Træning løst

En genstand tabes fra tilstrækkelig højde. Find hastighed efter 1,25 sekund.

Svar

v_eller = 0, da objektet er droppet, så:

v_F = gt = 9,8 x 1,25 m / s = 12,25 m / s, rettet lodret mod jorden. (Den lodrette nedadgående retning er taget som positiv).

Når objektet nærmer sig jorden, øges dets hastighed med 9,8 m / s for hvert forløbne sekund. Objektets masse er ikke involveret. To forskellige objekter, der falder fra samme højde og på samme tid, udvikler den samme hastighed, som de falder.

Referencer

1. Giancoli, D. Fysik. Principper med applikationer. Sjette udgave. Prentice Hall. 21-35.
2. Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 20-34.
3. Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7^mor. Udgave. Mexico. Cengage Learning Editors. 21-39.