Elastiske stød i en dimension, specielle tilfælde, øvelser

Det elastiske stød eller elastiske kollisioner består af korte, men intense interaktioner mellem objekter, hvor både momentum og kinetisk energi bevares. Nedbrud er meget hyppige begivenheder i naturen: fra subatomære partikler til galakser til billardkugler og kofangerbiler i forlystelsesparker, de er alle genstande, der kan kollidere.

Under en kollision eller kollision er interaktionskræfterne mellem objekter meget stærke, meget mere end dem, der kan handle eksternt. På denne måde kan det siges, at partiklerne under kollisionen danner et isoleret system.

I dette tilfælde er det rigtigt, at:

P_eller = P_F

Mængden af ​​bevægelse P_eller før kollisionen er den samme som efter kollisionen. Dette gælder for enhver form for kollision, både elastisk og uelastisk..

Overvej nu følgende: under en kollision gennemgår genstande en vis deformation. Når chokket er elastisk, genvinder genstande hurtigt deres oprindelige form.

Artikelindeks

• 1 Bevaring af kinetisk energi
• 2 Elastiske stød i en dimension
  • 2.1 -Formler til elastiske kollisioner
• 3 Særtilfælde i elastiske kollisioner
  • 3.1 To identiske masser
  • 3.2 To identiske masser, hvoraf den ene oprindeligt var i ro
  • 3.3 To forskellige masser, hvoraf den ene oprindeligt var i ro
• 4 Restitutionskoefficient eller Huygens-Newton-reglen
• 5 Øvelser løst
  • 5.1 -Løst øvelse 1
  • 5.2 -Løst øvelse 2
  • 5.3 -Løst øvelse 3
  • 5.4 -Løst øvelse 4
• 6 Referencer

Bevaring af kinetisk energi

Normalt under et nedbrud bruges en del af genstandens energi til varme, deformation, lyd og undertiden endda til at producere lys. Så den kinetiske energi i systemet efter kollisionen er mindre end den oprindelige kinetiske energi.

Når den kinetiske energi K bevares, så:

K_eller = K_F

Hvilket betyder, at de kræfter, der virker under kollisionen, er konservative. Under kollisionen omdannes den kinetiske energi kortvarigt til potentiel energi og derefter tilbage til kinetisk energi. De respektive kinetiske energier varierer, men summen forbliver konstant.

Perfekt elastiske kollisioner er sjældne, selv om billardkugler er en forholdsvis god tilnærmelse, ligesom kollisioner, der forekommer mellem ideelle gasmolekyler..

Elastiske stød i en dimension

Lad os undersøge en kollision af to partikler af dette i en enkelt dimension; det vil sige de interagerende partikler bevæger sig f.eks. langs x-aksen. Antag at de har masser m₁ Y m_to. De indledende hastigheder for hver er eller₁ Y eller_to henholdsvis. Endelige hastigheder er v₁ Y v_to.

Vi kan dispensere med vektornotationen, da bevægelsen udføres langs x-aksen, men tegnene (-) og (+) indikerer bevægelsesretningen. Til venstre er negativ og til højre positiv efter konvention.

-Formler til elastiske kollisioner

For bevægelsesmængden

m₁eller₁ + m_toeller_to = m₁v₁ + m_tov_to

Til kinetisk energi

½ m₁eller^to₁ + ½ m_toeller^to_to = ½ m₁v^to₁ +  ½ m_tov^to_to

Forudsat at masserne og de indledende hastigheder er kendt, kan ligningerne omgrupperes for at finde de endelige hastigheder.

Problemet er, at det i princippet er nødvendigt at udføre en lidt kedelig algebra, da ligningerne for kinetisk energi indeholder kvadraterne for hastighederne, hvilket gør beregningen lidt besværlig. Det ideelle ville være at finde udtryk, der ikke indeholder dem.

Den første ting er at undvære faktoren ½ og omarrangere begge ligninger på en sådan måde, at der vises et negativt tegn, og masserne kan tages med i beregningen:

m₁eller₁ - m₁v₁ = M_tov_to - m_toeller_to

m₁eller^to₁ - m₁v^to₁  = + M_tov^to_to - m_toeller^to_to

At blive udtrykt på denne måde:

m₁(eller₁ - v₁ ) = m_to(v_to - eller_to)

m₁(eller^to₁ - v^to₁ ) = m_to (v^to_to - eller^to_to)

Forenkling for at eliminere kvadraterne i hastighederne

Nu skal vi gøre brug af produktets bemærkelsesværdige sum ved dens forskel i den anden ligning, hvormed vi får et udtryk, der ikke indeholder kvadraterne, som oprindeligt ønsket:

m₁(eller₁ - v₁ ) = m_to(v_to - eller_to)

m₁(eller₁ - v₁ ) (eller₁ + v₁ ) = m_to (v_to - eller_to) (v_to + eller_to)

Det næste trin er at erstatte den første ligning i den anden:

m_to(v_to - eller_to) (eller₁ + v₁ ) = m_to (v_to - eller_to) (v_to + eller_to)

Og når udtrykket gentages m_to(v_to - eller_to) på begge sider af ligestillingen annulleres den nævnte periode og ser sådan ud:

(eller₁ + v₁) = (v_to + eller_to)

Eller endnu bedre:

eller₁ - eller_to= v_to -  v₁

Endelige hastigheder v₁ og V_to af partiklerne

Nu har du to lineære ligninger, der er lettere at arbejde med. Vi sætter dem tilbage den ene under den anden:

m₁eller₁ + m_toeller_to = m₁v₁ + m_tov_to

eller₁ - eller_to= v_to -  v₁

Multiplicere den anden ligning med m₁ og tilføjelse af term til term er:

m₁eller₁ + m_toeller_to = m₁v₁ + m_tov_to

m₁eller₁ - m₁eller_to= m₁v_to - m₁ v₁

-

2 m₁eller₁ + (m_to - m₁) eller_to = (m_to + m₁) v_to

Og det er allerede muligt at rydde v_to. For eksempel:

Særlige tilfælde ved elastiske kollisioner

Nu hvor ligninger er tilgængelige for de endelige hastigheder for begge partikler, er det tid til at analysere nogle specielle situationer.

To identiske masser

Derefter m₁ = m_to = m Y:

v₁ = u_to

v_to = u₁

Partiklerne udveksler simpelthen deres hastigheder efter kollisionen.

To identiske masser, hvoraf den ene oprindeligt var i ro

Igen  m₁ = m_to = m og antager det eller₁ = 0:

v₁ = u_to

v_to = 0

Efter kollisionen får den partikel, der var i ro, den samme hastighed som den partikel, der bevægede sig, og dette stopper igen.

To forskellige masser, en af ​​dem oprindeligt i hvile

Antag i dette tilfælde det eller₁ = 0, men masserne er forskellige:

Hvad hvis m₁ er meget større end m_to?

Det sker, at m₁ er stadig i ro og m_to vender tilbage så hurtigt som det ramte.

Restitutionskoefficient eller Huygens-Newton-reglen

Tidligere blev følgende forhold mellem hastighederne afledt for to objekter i elastisk kollision: eller₁ - eller_to = v_to -  v₁. Disse forskelle er de relative hastigheder før og efter kollisionen. Generelt gælder det for en kollision, at:

eller₁ - eller_to = - (v₁ -  v_to)

Begrebet relativ hastighed værdsættes bedst, hvis læseren forestiller sig, at han befinder sig på en af ​​partiklerne, og fra denne position observerer han den hastighed, hvormed den anden partikel bevæger sig. Ovenstående ligning omskrives således:

Løst øvelser

-Løst øvelse 1

En billardkugle bevæger sig mod venstre ved 30 cm / s og kolliderer frontalt med en anden identisk kugle, der bevæger sig til højre ved 20 cm / s. De to kugler har samme masse, og kollisionen er perfekt elastisk. Finde hastigheden på hver kugle efter stød.

Opløsning

eller₁ = -30 cm / s

eller_to = +20 cm / s

Det er det specielle tilfælde, hvor to identiske masser kolliderer elastisk i en dimension, hvorfor hastighederne udveksles.

v₁ = +20 cm / s

v_to = -30 cm / s

-Træning løst 2

Restitutionskoefficienten for en bold, der hopper ned fra jorden, er lig med 0,82. Hvis den falder fra hvile, hvilken brøkdel af dens oprindelige højde når bolden efter at have hoppet en gang? Og efter 3 hopp?

Opløsning

Jord kan være objekt 1 i koefficienten for restitutionligning. Og det forbliver altid i ro, så:

Med denne hastighed hopper den:

+ Tegnet angiver, at det er en stigende hastighed. Og ifølge det når bolden en maksimal højde på:

Nu vender den tilbage til jorden igen med en hastighed af samme størrelse, men det modsatte tegn:

Dette opnår en maksimal højde på:

Gå tilbage til jorden med:

Efterfølgende hopp

Hver gang bolden hopper og stiger, skal du gange hastigheden igen med 0,82:

Nu er h₃ er ca. 30% af h_eller. Hvad ville være højden til det 6. hopp uden behov for at foretage så detaljerede beregninger som de foregående?

Ville det h₆ = 0,82¹² h_eller = 0,092 timer_eller eller kun 9% af h_eller.

-Træning løst 3

En blok på 300 g bevæger sig nordpå ved 50 cm / s og kolliderer med en 200 g blok mod syd ved 100 cm / s. Antag, at chokket er helt elastisk. Find hastighederne efter stød.

Data

m₁ = 300 g; eller₁ = + 50 cm / s

m_to = 200 g; eller_to = -100 cm / s

-Træning løst 4

En masse på m frigives₁ = 4 kg fra det angivne punkt på det friktionsfrie spor, indtil det kolliderer med m_to = 10 kg i hvile. Hvor høj stiger m?₁ efter kollisionen?

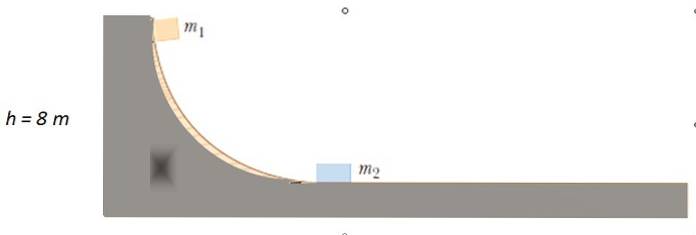
Opløsning

Da der ikke er nogen friktion, bevares mekanisk energi for at finde hastigheden eller₁ Med hvad m₁ påvirkninger  m_to. Oprindeligt er den kinetiske energi 0, siden m₁ del af hvile. Når den bevæger sig på den vandrette overflade, har den ingen højde, så den potentielle energi er 0.

mgh = ½ mu₁ ^to

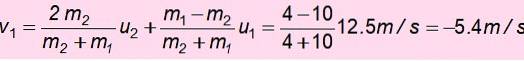
eller_to = 0

Nu er hastigheden på m₁ efter kollisionen:

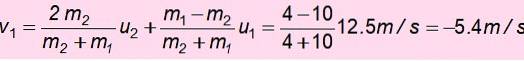
Det negative tegn betyder, at det er returneret. Med denne hastighed stiger den, og den mekaniske energi bevares igen for at finde h ', den højde, som du kan stige op efter styrtet:

½ mv₁^to = mgh '

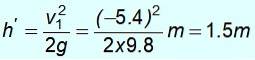
Bemærk, at det ikke vender tilbage til startpunktet i en højde på 8 m. Det har ikke nok energi, fordi massen gav en del af sin kinetiske energi m_1.

Referencer

1. Giancoli, D. 2006. Fysik: Principper med applikationer. 6^th. Ed Prentice Hall. 175-181
2. Rex, A. 2011. Grundlæggende fysik. Pearson. 135-155.
3. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^na Cengage læring. 172-182
4. Tipler, P. (2006) Fysik til videnskab og teknologi. 5. udg. Bind 1. Editorial Reverté. 217-238
5. Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. MacGraw Hill. 185-195