
Brayton-cyklusproces, effektivitet, applikationer, øvelser
Det Brayton cyklus er en termodynamisk cyklus, der består af fire processer og påføres en komprimerbar termodynamisk væske såsom en gas. Dens første omtale stammer fra slutningen af det 18. århundrede, selvom det var nogen tid, før det først blev rejst af James Joule. Derfor er det også kendt som Joule-cyklus..
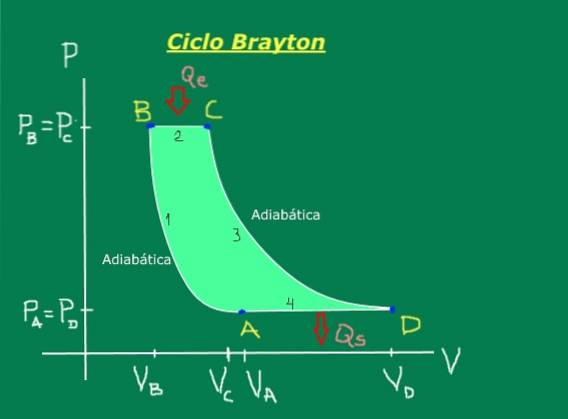
Den består af følgende trin, som bekvemt illustreres i tryk-volumen-diagrammet i figur 1: adiabatisk kompression (ingen varme udveksles), isobar ekspansion (forekommer ved konstant tryk), adiabatisk ekspansion (ingen varme udveksles) og isobar kompression (forekommer ved konstant tryk).
Artikelindeks
- 1 Proces og beskrivelse
- 1.1 Adgang
- 1.2 Kompression
- 1.3 Forbrænding
- 1.4 Udvidelse
- 1.5 Udstødning
- 2 Effektivitet som funktion af temperatur, varme og tryk
- 2.1 Indgående varme, udgående varme og effektivitet
- 2.2 Varme og tryk i Brayton-cyklussen
- 2.3 Forenklet resultat
- 2.4 Effektivitet som funktion af trykforholdet
- 3 applikationer
- 4 Løst øvelser
- 4.1-Øvelse 1
- 4.2-Øvelse 2
- 5 Referencer
Proces og beskrivelse
Brayton-cyklussen er den ideelle termodynamiske cyklus, der bedst anvendes til at forklare den termodynamiske drift af gasturbiner og luft-brændstofblanding, der bruges til generering af elektrisk energi og i flymotorer.
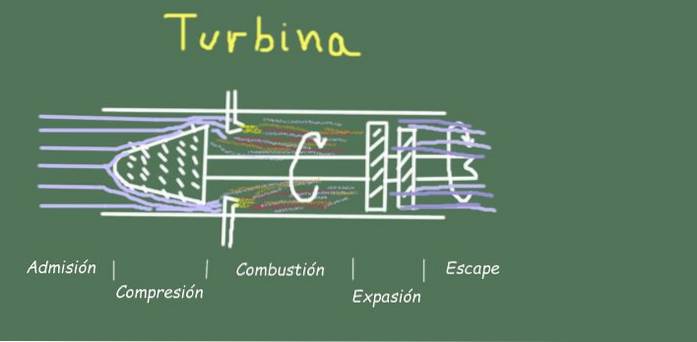
For eksempel er der i driften af en turbine flere trin i den operationelle gasstrøm, som vi vil se nedenfor.
Adgang
Den består af luftindgang ved omgivelsestemperatur og tryk gennem turbinens indgangsåbning.
Kompression
Luft komprimeres ved at rotere vinger mod faste vinger i turbinens kompressorsektion. Denne kompression er så hurtig, at der praktisk talt ikke er nogen varmeveksling, så den er modelleret af den adiabatiske proces AB i Brayton-cyklussen. Luften ved kompressorudgangen har øget sit tryk og temperatur.
Forbrænding
Luften blandes med propangas eller pulveriseret brændstof, der indføres gennem injektorerne i forbrændingskammeret. Blandingen frembringer en kemisk reaktion med forbrænding.
Denne reaktion er, hvad der giver varmen, der øger temperaturen og den kinetiske energi af de gaspartikler, der ekspanderer i forbrændingskammeret ved konstant tryk. I Brayton-cyklussen er dette trin modelleret med BC-processen, der finder sted ved konstant tryk.
Udvidelse
I selve sektionen af turbinen ekspanderer luft fortsat mod turbinebladene, hvilket får den til at rotere og frembringe mekanisk arbejde. I dette trin sænker luften sin temperatur, men uden praktisk at udveksle varme med miljøet..
I Brayton-cyklussen simuleres dette trin som en CD-adiabatisk udvidelsesproces. En del af turbinens arbejde overføres til kompressoren, og den anden bruges til at drive en generator eller propel.
Flugt
Den udgående luft har et konstant tryk svarende til det omgivende tryk og overfører varme til den enorme masse af udvendig luft, så det tager på kort tid den samme temperatur som indgangsluften. I Brayton-cyklussen simuleres dette trin med DA-processen med konstant tryk, der lukker den termodynamiske cyklus.
Effektivitet som funktion af temperatur, varme og tryk
Vi foreslår at beregne effektiviteten af Brayton-cyklussen, for hvilken vi starter med definitionen af den.
I en varmemotor defineres effektivitet som maskinens nettoarbejde divideret med den leverede varmeenergi.

Det første princip for termodynamik siger, at nettovarmen, der bidrager til en gas i en termodynamisk proces, er lig med ændringen i den indre energi af gassen plus det arbejde, den udfører..
Men i en komplet cyklus er variationen af den indre energi nul, så den nettovarme, der tilføres i cyklussen, er lig med det udførte nettoarbejde..

Indgående varme, udgående varme og effektivitet
Det forrige udtryk giver os mulighed for at skrive effektiviteten som en funktion af den absorberede eller indkommende varme Qe (positiv) og den overførte eller udgående varme Qs (negativ).

Varme og tryk i Brayton-cyklussen
I Brayton-cyklussen kommer varme ind i den isobariske proces BC og ud i den isobare proces DA.
Antages det, at n mol gas ved konstant tryk forsynes med følsom varme Qe i proces BC, så stiger temperaturen fra Tb til Tc i henhold til følgende forhold:

Udgående varme Qs kan beregnes på samme måde ved hjælp af følgende forhold, der gælder for konstanttryksprocessen DA:

Ved at erstatte disse udtryk i det udtryk, der giver os effektiviteten som en funktion af den indgående varme og udgående varme, hvilket gør de relevante forenklinger, opnås følgende forhold for effektiviteten:

Forenklet resultat
Det er muligt at forenkle det tidligere resultat, hvis vi tager højde for det Pa = Pd Og hvad så Pb = Pc da processer AD og BC er isobariske, dvs. ved samme tryk.
Da processerne AB og CD er adiabatiske, opfyldes Poissons forhold også for begge processer:

Hvor gamma repræsenterer den adiabatiske kvotient, det vil sige kvotienten mellem varmekapaciteten ved konstant tryk og varmekapaciteten ved konstant volumen.
Ved hjælp af disse forhold og forholdet fra den ideelle gasligning af tilstand kan vi få et alternativt udtryk for Poissons forhold:

Hvordan ved vi det Pa = Pd Og hvad så Pb = Pc udskiftning og opdeling af medlem efter medlem opnås følgende forhold mellem temperaturer:

Hvis hvert medlem af den foregående ligning trækkes af enheden, løses forskellen, og vilkårene arrangeres, kan det vises, at:


Ydeevne som en funktion af trykforholdet
Udtrykket opnået for effektiviteten af Brayton-cyklussen som en funktion af temperaturer kan omskrives for at blive formuleret som en funktion af kvotienten af trykket ved kompressorens udløb og indløb.
Dette opnås, hvis Poissons forhold mellem punkterne A og B er kendt som en funktion af tryk og temperatur, idet man opnår, at effektiviteten af cyklussen udtrykkes som følger:

Et typisk trykforhold er 8. I dette tilfælde har Brayton-cyklussen et teoretisk udbytte på 45%..
Ansøgninger
Brayton-cyklussen som model anvendes på gasturbiner, der bruges i termoelektriske anlæg for at flytte generatorer, der producerer elektricitet.
Det er også en teoretisk model, der er velegnet til driften af turbopropmotorer, der anvendes i fly, men den kan slet ikke anvendes i flyturbojets..
Når du vil maksimere det arbejde, der produceres af turbinen for at flytte generatorerne eller propellerne til et fly, så anvendes Brayton-cyklussen..

På turbojet med fly er det derimod ikke interessant at konvertere forbrændingsgassernes kinetiske energi til at producere arbejde, hvilket ville være lige nok til at genoplade turboladeren.
Tværtimod er det vigtigt at opnå den højest mulige kinetiske energi af den udstødte gas, således at flyets momentum opnås ifølge handlings- og reaktionsprincippet..
Løst øvelser
-Øvelse 1
En gasturbine, der anvendes i termoelektriske kraftværker, har et tryk ved kompressorudløbet på 800 kPa. Den indkommende gastemperatur er omgivende og er 25 Celsius, og trykket er 100 kPa.
I forbrændingskammeret stiger temperaturen op til 1027 Celsius for at komme ind i turbinen.
Bestem cykluseffektiviteten, gastemperaturen ved kompressorudgangen og gastemperaturen ved turbineudgangen.
Opløsning
Da vi har trykket fra gassen ved kompressorens udløb, og vi ved, at indgangstrykket er atmosfærisk tryk, er det muligt at opnå trykforholdet:
r = Pb / Pa = 800 kPa / 100 KPa = 8
Da den gas, som turbinen arbejder med, er en blanding af luft og propangas, anvendes den adiabatiske koefficient derefter til en diatomisk idealgas, det vil sige en gamma på 1,4.
Effektiviteten beregnes derefter således:
Hvor vi har anvendt det forhold, der giver effektiviteten af Brayton-cyklussen som en funktion af trykforholdet i kompressoren.

Beregning af temperatur
For at bestemme temperaturen ved kompressorens udløb, eller hvad er den samme temperatur, som gassen kommer ind i forbrændingskammeret, anvender vi forholdet mellem effektiviteten og kompressorens ind- og udløbstemperaturer.
Hvis vi løser temperaturen Tb fra dette udtryk, opnår vi:

Som data for øvelsen har vi, at temperaturen efter forbrænding stiger til 1027 Celsius for at komme ind i turbinen. En del af gassens termiske energi bruges til at flytte turbinen, så temperaturen ved dens udløb skal være lavere.
For at beregne temperaturen ved turbinens udløb vil vi bruge et forhold mellem tidligere opnået temperatur:

Derfra løser vi for Td for at opnå temperaturen ved turbinens udløb. Efter udførelse af beregningerne er den opnåede temperatur:
Td = 143,05 Celsius.
-Øvelse 2
En gasturbine følger Brayton-cyklussen. Trykforholdet mellem kompressorens indgang og udløb er 12.
Antag omgivelsestemperaturen på 300 K. Som yderligere data er det kendt, at temperaturen på gassen efter forbrænding (før den kommer ind i turbinen) er 1000 K.
Bestem temperaturen ved kompressorens udløb og temperaturen ved turbinens udløb. Bestem også, hvor mange kilo gas der cirkulerer gennem turbinen i hvert sekund, idet du ved, at dens effekt er 30 KW.
Antag gassens specifikke varme som konstant og tag dens værdi ved stuetemperatur: Cp = 1,0035 J / (kg K).
Antag også, at kompressionseffektiviteten i kompressoren og dekompressionseffektiviteten i turbinen er 100%, hvilket er en idealisering, fordi der i praksis altid opstår tab..
Opløsning
For at bestemme temperaturen ved kompressorudgangen, idet vi kender indløbstemperaturen, skal vi huske, at det er en adiabatisk kompression, så Poissons forhold kan anvendes til AB-processen.



For enhver termodynamisk cyklus vil nettearbejdet altid svare til nettovarmen, der udveksles i cyklussen..

Nettoarbejdet pr. Driftscyklus kan derefter udtrykkes som en funktion af massen af gas, der cirkulerede i denne cyklus, og temperaturerne.

I dette udtryk m er den gasmasse, der cirkulerer gennem turbinen i en driftscyklus og Cp specifik varme.
Hvis vi tager det afledte med hensyn til tidspunktet for det foregående udtryk, opnår vi netto middeleffekten som en funktion af massestrømmen.

Rydder ud m punkt, og ved at erstatte temperaturerne, kraften og varmekapaciteten for gassen opnår vi en massestrøm på 1578,4 kg / s.
Referencer
- Alfaro, J. Thermodynamic Cycles. Gendannet fra: fis.puc.cl.
- Fernandez J.F. Brayton cyklus. Gasturbine. U.T.N. (Mendoza). Gendannet fra: edutecne.utn.edu.ar.
- Sevilla Universitet. Fysikafdeling. Brayton cyklus. Gendannet fra: laplace.us.es.
- Táchira National Experimental University. Transportfenomener. Gaseffektcyklusser. Gendannet fra: unet.edu.ve.
- Wikipedia. Brayton cyklus. Gendannet fra: wikiwand.com
- Wikipedia. Gasturbine. Gendannet fra: wikiwand.com.



Endnu ingen kommentarer