
Konstant proportionalitet, hvad er det, beregning, øvelser
Det konstant af proportionalitet Det er et relationelt numerisk element, der bruges til at definere mønsteret for lighed mellem 2 størrelser, der ændres samtidigt. Det er meget almindeligt at repræsentere det som en lineær funktion på en generisk måde ved hjælp af udtrykket F (X) = k.X. Dette er imidlertid ikke den eneste repræsentation af en mulig proportionalitet.
For eksempel har forholdet mellem X og Y i funktionen Y = 3x en konstant proportionalitet lig med 3. Det observeres, at når den uafhængige variabel X vokser, så gør den afhængige variabel Y, tredoblet sin værdi tidligere.
Ændringerne anvendt på den ene variabel har øjeblikkelige konsekvenser for den anden, så der er en værdi kendt som proportionalitetskonstanten. Dette tjener til at relatere de forskellige størrelser, som begge variabler erhverver.
Artikelindeks
- 1 Hvad er konstanten af proportionalitet og typer
- 1.1 Direkte proportionalitet
- 1.2 Omvendt eller indirekte proportionalitet
- 2 Hvordan beregnes det?
- 2.1 Ifølge dens graf
- 2.2 I henhold til værditabellen
- 2.3 Ifølge analytisk udtryk
- 2.4 Ved direkte eller sammensat regel på tre
- 3 Historie
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Hvad er konstanten af proportionalitet og typer
I henhold til tendensen i ændringen af variablerne kan proportionaliteterne klassificeres i 2 typer.
Direkte proportionalitet
Foreslår et envejsforhold mellem to størrelser. I den, hvis den uafhængige variabel viser en vis vækst, vil den afhængige variabel også vokse. Tilsvarende vil ethvert fald i den uafhængige variabel medføre et fald i størrelsen af Y.
For eksempel den lineære funktion, der blev brugt i indledningen; Y = 3X, svarer til et direkte forhold mellem proportionalitet. Dette skyldes, at stigningen i den uafhængige variabel X vil medføre en tredobling af den tidligere værdi taget af den afhængige variabel Y.
På samme måde falder den afhængige variabel tre gange sin værdi, når X falder i størrelse.
Værdien af proportionalitetskonstanten "K" i et direkte forhold defineres som K = Y / X.
Omvendt eller indirekte proportionalitet
I denne type funktioner præsenteres forholdet mellem variablerne antonymt, hvor væksten eller faldet af den uafhængige variabel svarer til henholdsvis faldet eller væksten af den afhængige variabel..
For eksempel er funktionen F (x) = k / x et omvendt eller indirekte forhold. Da værdien af den uafhængige variabel begynder at stige, divideres værdien af k med et stigende antal, hvilket får den afhængige variabel til at falde i værdi i forhold til andelen.
Afhængig af værdien taget af K kan tendensen for den inverse proportionale funktion defineres. Hvis k> 0, falder funktionen på alle reelle tal. Og dens graf vil være i 1. og 3. kvadrant.
Tværtimod, hvis værdien af K er negativ eller mindre end nul, vil funktionen stige, og dens graf findes i 2. og 4. kvadrant.
Hvordan beregnes det?
Der er forskellige sammenhænge, hvor definitionen af proportionalitetskonstanten kan være påkrævet. I de forskellige tilfælde vises forskellige data om problemet, hvor undersøgelsen af disse endelig giver værdien af K.
På en generisk måde kan ovennævnte rekapituleres. Værdierne af K svarer til to udtryk afhængigt af den tilstedeværende proportionalitetstype:
- Direkte: K = Y / X
- Omvendt eller indirekte: K = Y.X
Ifølge dens graf
Nogle gange er grafen for en funktion kun delvis eller fuldstændig kendt. I disse tilfælde vil det være nødvendigt ved hjælp af grafisk analyse at bestemme typen af proportionalitet. Derefter bliver det nødvendigt at definere en koordinat, der gør det muligt at verificere værdierne for X og Y for at gælde for den tilsvarende formel for K.
Graferne, der henviser til direkte proportionaliteter, er lineære. På den anden side tager graferne af inverse proportionale funktioner normalt form af hyperboler.
Ifølge værditabellen
I nogle tilfælde er der en tabel over værdier med de værdier, der svarer til hver iteration af den uafhængige variabel. Normalt indebærer dette realiseringen af grafen ud over at definere værdien af K.
Ifølge analytisk udtryk
Returnerer det udtryk, der definerer funktionen analytisk. Værdien af K kan løses direkte, eller den kan også udledes fra selve udtrykket.
Ved direkte eller sammensat regel på tre
I andre øvelsesmodeller præsenteres visse data, der henviser til forholdet mellem værdierne. Dette gør det nødvendigt at anvende den direkte eller sammensatte regel på tre for at definere andre nødvendige data i øvelsen..
Historie
Begrebet proportionalitet har altid eksisteret. Ikke kun i de store matematikers sind og arbejde, men i befolkningens daglige liv på grund af dets praktiske og anvendelige.
Det er meget almindeligt at finde situationer, der kræver en proportionalitetsmetode. Disse præsenteres i hvert tilfælde, hvor det er nødvendigt at sammenligne variabler og fænomener, der har visse sammenhænge.
Gennem en tidslinje kan vi karakterisere de historiske øjeblikke, hvor matematiske fremskridt med hensyn til proportionalitet er blevet anvendt..
- 2. århundrede f.Kr. Brøkdel- og andelslagringssystemet er vedtaget i Grækenland.
- 5. århundrede f.Kr. Andelen, der relaterer til siden og diagonalen på en firkant, findes også i Grækenland.
- 600 f.Kr. Thales of Miletus præsenterer sin sætning om proportionalitet.
- År 900. Det decimalsystem, der tidligere blev brugt af Indien, udvides i forhold og proportioner. Bidrag fra araberne.
- XVII århundrede. Bidrag vedrørende proportionerne ankommer til Eulers beregning.
- XIX århundrede. Gauss bidrager med begrebet kompleks antal og andel.
- Tyvende århundrede. Proportionalitet som en funktionsmodel er defineret af Azcarate og Deulofeo.

Løst øvelser
Øvelse 1
Det er nødvendigt at beregne værdien af variablerne x, y, z og g. Kendskab til følgende forholdsmæssige forhold:
3x + 2y - 6z + 8g = 1925
x / 3 = y / 8 = z / 3 = g / 5
Vi fortsætter med at definere de relative værdier af proportionalitetskonstanten. Disse kan fås fra det andet forhold, hvor værdien, der deler hver variabel, indikerer et forhold eller et forhold, der henviser til K.
X = 3k y = 2k z = 3k g = 5k
Værdierne erstattes i det første udtryk, hvor det nye system evalueres i en enkelt variabel k.
3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925
9k + 4k -18k + 40k = 1925
35k = 1925
K = 1925/35 = 55
Ved hjælp af denne værdi af proportionalitetskonstanten kan vi finde figuren, der definerer hver af variablerne.
x = 3 (55) = 165 y = 2 (55) = 110
z = 3 (55) = 165 g = 5 (55) = 275
Øvelse 2
Beregn proportionalitetskonstanten og det udtryk, der definerer funktionen, givet dens graf.
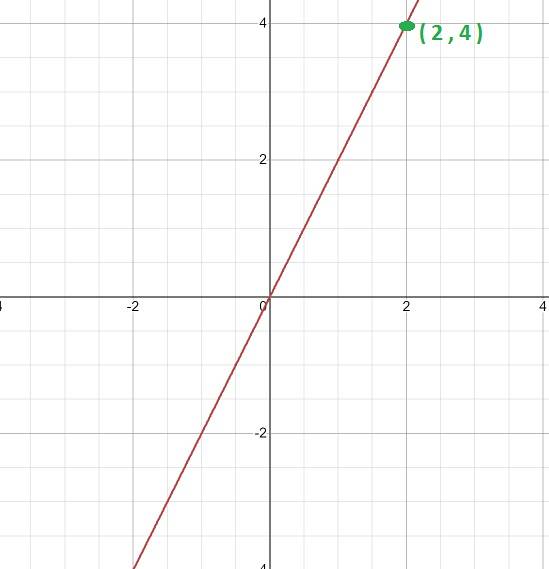
For det første analyseres grafen, idet dens lineære karakter er tydelig. Dette indikerer, at det er en funktion med direkte proportionalitet, og at værdien af K opnås gennem udtrykket k = y / x
Derefter vælges et bestemt punkt fra grafen, det vil sige et punkt, hvor koordinaterne, der komponerer det, kan ses nøjagtigt..
I dette tilfælde tages punktet (2, 4). Fra hvor vi kan etablere følgende forhold.
K = 4/2 = 2
Så udtrykket er defineret af funktionen y = kx, som i dette tilfælde vil være
F (x) = 2x
Referencer
- Matematik for elektricitet og elektronik. Dr. Arthur Kramer. Cengage Learning, 27. juli 2012
- Vision 2020: Den strategiske rolle i operationel forskning. N. Ravichandran. Allied Publishers, 11. september. 2005
- Grammatik og aritmetisk viden om statens administrative assistent. E-bog. MAD-Eduforma
- Forstærkning af matematik til støtte og diversificering af læseplaner: til støtte og diversificering af læseplaner. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29. august. 2003
- Logistik og kommerciel ledelse. Maria José Escudero Serrano. Ediciones Paraninfo, S.A., 1. sept. 2013


Endnu ingen kommentarer