
Cylindriske koordinatsystem, ændringer og øvelser
Det cylindriske koordinater de tjener til at lokalisere punkter i et tredimensionelt rum og består af en radial koordinat ρ, en azimutkoordinat φ og en højdekoordinat z.
En pointe P placeret i rummet projiceres vinkelret på flyet XY giver anledning til pointen P ' i det fly. Afstanden fra oprindelsen til punktet P ' definerer koordinaten ρ, mens vinklen dannes af aksen x med strålen OP ' definerer koordinaten φ. Endelig koordinaten z er punktets vinkelrette projektion P på aksen Z. (se figur 1).
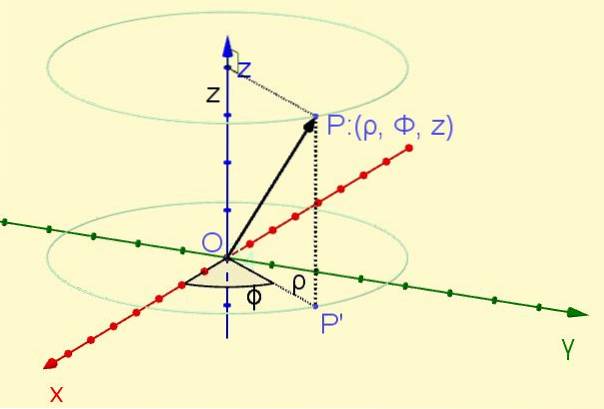
Den radiale koordinat ρ er altid positiv, den azimutale koordinat φ varierer fra nul radianer til to pi radianer, mens z-koordinaten kan have en hvilken som helst reel værdi:
0 ≤ ρ < ∞
0 ≤ φ < 2π
- ∞ < z < + ∞
Artikelindeks
- 1 Ændring af koordinater
- 1.1 Vektorbase i cylindriske koordinater
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 3.4 Øvelse 4
- 4 Referencer
Ændring af koordinater
Det er relativt let at få de kartesiske koordinater (x, y, z) til et punkt P fra dets cylindriske koordinater (ρ, φ, z):
x = ρ cos (φ)
y = ρ sin (φ)
z = z
Men det er også muligt at opnå de polære koordinater (ρ, φ, z) ud fra kendskabet til de kartesiske koordinater (x, y, z) for et punkt P:
ρ = √ (xto + Yto)
φ = arctan (y / x)
z = z
Vektor base i cylindriske koordinater
Basen på cylindriske enhedsvektorer er defineret Uρ, Uφ, Uz.
Vektoren Uρ er tangent til linjen φ = ctte og z = ctte (peger radialt udad), vektoren Uφ er tangent til linjen ρ = ctte og z = ctte og til sidst Uz har samme retning af Z-aksen.
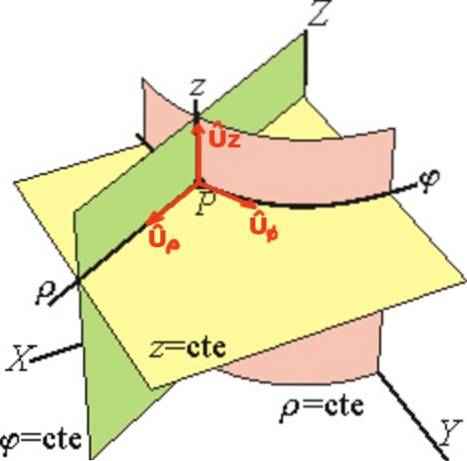
I den cylindriske enhedsbase er positionsvektoren r af et punkt P er skrevet vektorisk sådan:
r = ρ Uρ + 0 Uφ + z Uz
På den anden side er en uendelig minimal forskydning dr fra punkt P udtrykkes det som følger:
dr = dρ Uρ + ρ dφ Uφ + dz Uz
Tilsvarende er et uendeligt lille element af volumen dV i cylindriske koordinater:
dV = ρ dρ dφ dz
Eksempler
Der er utallige eksempler på anvendelse og anvendelse af cylindriske koordinater. I kartografi f.eks cylindrisk fremspring, baseret netop på disse koordinater. Der er flere eksempler:
Eksempel 1
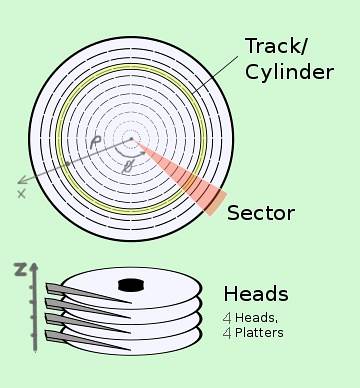
Cylindriske koordinater har anvendelser inden for teknologi. Som et eksempel har vi CHS-systemet (Cylinder-Head-Sector) til lokalisering af data på en harddisk, som faktisk består af flere diske:
- Cylinderen eller sporet svarer til koordinaten ρ.
- Sektoren svarer til positionen φ på den disk, der roterer højt Vinkelhastighed.
- Hovedet svarer til z-positionen af læsehovedet på den tilsvarende disk.
Hver informationsbyte har en præcis adresse i cylindriske koordinater (C, S, H).
Eksempel 2
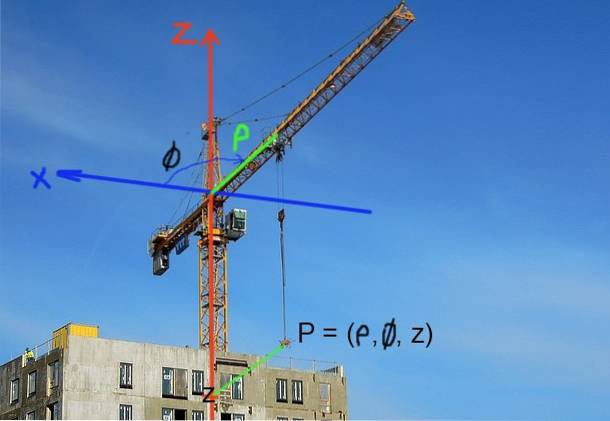
Konstruktionskraner fastgør lastens position i cylindriske koordinater. Den vandrette position defineres af afstanden til kranens ρ akse eller pil og af dens vinkelposition φ i forhold til en eller anden referenceakse. Lastens lodrette position bestemmes af z-koordinaten for højden.
Løst øvelser
Øvelse 1
Der er punkter P1 med cylindriske koordinater (3, 120º, -4) og punkt P2 med cylindriske koordinater (2, 90º, 5). Find Euklidisk afstand mellem disse to punkter.
Opløsning: Først fortsætter vi med at finde de kartesiske koordinater for hvert punkt i henhold til formlen ovenfor.
P1 = (3 * cos 120º, 3 * sin 120º, -4) = (-1,5, 2,60, -4)
P2 = (2 * cos 90º, 2 * sin 90º, 5) = (0, 2, 5)
Den euklidiske afstand mellem P1 og P2 er:
d (P1, P2) = √ ((0 - (-1,5))to+(2 - 2,60)to+(5 - (- 4))to ) = ...
… √ (2,25 + 0,36 + 81) = 9,14
Øvelse 2
Punkt P har kartesiske koordinater (-3, 4, 2). Find de tilsvarende cylindriske koordinater.
Opløsning: Vi fortsætter med at finde de cylindriske koordinater ved hjælp af forholdet ovenfor:
ρ = √ (xto + Yto) = √ ((- 3)to + 4to) = √ (9 + 16) = √ (25) = 5
φ = arctan (y / x) = arctan (4 / (- 3)) = -53,13 º + 180 º = 126,87 º
z = 2
Det skal huskes, at den arktangente funktion er multiværdier med 180º periodicitet. Vinklen φ skal også høre til den anden kvadrant, da x- og y-koordinaterne for punkt P er i den kvadrant. Dette er grunden til, at 180 ° er blevet tilføjet til resultatet φ.
Øvelse 3
Udtrykkes i cylindriske koordinater og i kartesiske koordinater overfladen af en cylinder med radius 2, og hvis akse falder sammen med Z-aksen.
Løsning: Det forstås, at cylinderen har en uendelig forlængelse i z-retning, så ligningen af overfladen i cylindriske koordinater er:
ρ = 2
For at opnå den cartesiske ligning af den cylindriske overflade tages kvadratet for begge medlemmer af den foregående ligning:
ρto = 4
Vi ganger med 1 begge medlemmer af den tidligere ligestilling og anvender grundlæggende trigonometrisk identitet (sento(φ) + costo(φ) = 1):
1 * ρto = 1 * 4
(sento(φ) + costo(φ)) * ρto = 1 * 4
Parentesen er udviklet til at opnå:
(ρ sin (φ))to + (ρ cos (φ))to = 4
Vi husker, at de første parenteser (ρ sin (φ)) er y-koordinaten for et punkt i polære koordinater, mens parenteserne (ρ cos (φ)) repræsenterer x-koordinaten, så vi har ligningen af cylinderen i kartesiske koordinater:
Yto + xto = 2to
Den forrige ligning bør ikke forveksles med en cirkel i XY-planet, da det i dette tilfælde vil se sådan ud: yto + xto = 2to ; z = 0.
Øvelse 4
En cylinder med radius R = 1 m og højde H = 1m har sin masse fordelt radialt i henhold til følgende ligning D (ρ) = C (1 - ρ / R) hvor C er en konstant med værdien C = 1 kg / m3. Find cylinderens samlede masse i kg.
Opløsning: Den første ting er at indse, at funktionen D (ρ) repræsenterer den volumetriske massedensitet, og at massetætheden fordeles i cylindriske skaller med faldende densitet fra centrum til periferien. Et uendeligt lille volumenelement i henhold til problemets symmetri er:
dV = ρ dρ 2π H
Derfor vil den uendelige masse af en cylindrisk skal være:
dM = D (ρ) dV
Derfor vil den samlede masse af cylinderen blive udtrykt ved følgende bestemt integral:
M = ∫ellerR D (ρ) dV = ∫ellerR C (1 - ρ / R) ρ dρ 2π H = 2π H C ∫ellerR (1 - ρ / R) ρ dρ
Løsningen af den angivne integral er ikke vanskelig at opnå, hvis resultat er:
∫ellerR (1 - ρ / R) ρ dρ = (⅙) Rto
Ved at inkorporere dette resultat i udtrykket af cylindermassen får vi:
M = 2π H C (⅙) Rto = ⅓ π H C Rto =
⅓ π 1m * 1kg / m3* 1mto = π / 3 kg ≈ 1,05 kg
Referencer
- Arfken G og Weber H. (2012). Matematiske metoder til fysikere. En omfattende guide. 7. udgave. Akademisk presse. ISBN 978-0-12-384654-9
- Beregning cc. Løste problemer med cylindriske og sfæriske koordinater. Gendannet fra: calculo.cc
- Weisstein, Eric W. "Cylindriske koordinater." Fra MathWorld-A Wolfram Web. Gendannet fra: mathworld.wolfram.com
- wikipedia. Cylindrisk koordinatsystem. Gendannet fra: en.wikipedia.com
- wikipedia. Vektorfelter i cylindriske og sfæriske koordinater. Gendannet fra: en.wikipedia.com



Endnu ingen kommentarer