Sfæriske koordinater eksempler og løste øvelser

Det sfæriske koordinater er et punktplaceringssystem i et tredimensionelt rum bestående af en radial koordinat og to vinkelkoordinater kaldet polarkoordinat og azimutkoordinat.

Figur 1, som vi ser nedenfor, viser de sfæriske koordinater (r, θ, φ) for et punkt M. Disse koordinater henvises til et ortogonalt system af kartesiske akser X, Y, Z med oprindelse O.

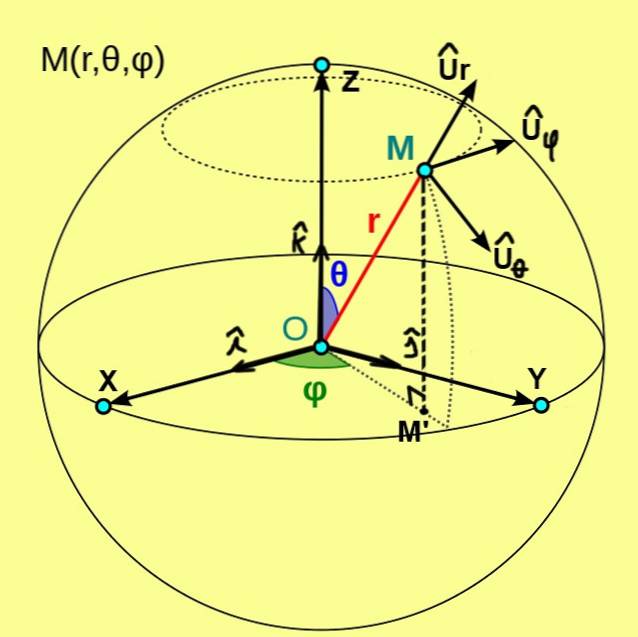
I dette tilfælde er koordinaten r for punkt M afstanden fra dette punkt til oprindelsen O. Polarkoordinaten θ repræsenterer vinklen mellem den positive halvakse Z og radiusvektoren OM. Mens den azimutale koordinat φ er vinklen mellem den positive halvakse X og radiusvektoren OM ', hvor M' er den ortogonale projektion af M på XY-planet.

Den radiale koordinat r tager kun positive værdier, men hvis et punkt er placeret ved oprindelsen, er r = 0. Den polære koordinat θ tager som minimum 0 ° for punkter placeret på den positive Z-halvakse og en maksimumsværdi 180 ° for punkterne er placeret på den negative Z-halvakse. Endelig tager azimutkoordinaten φ som minimum 0 ° og en maksimal højde på 360º.

0 ≤ r < ∞

0 ≤ θ ≤ 180º

0 ≤ φ  < 360º

Artikelindeks

• 1 Ændring af koordinater
  • 1.1 Vektorbase i sfæriske koordinater
  • 1.2 Linie- og volumenelementer i sfæriske koordinater
• 2 Forhold til geografiske koordinater
  • 2.1 Formler til at skifte fra geografisk til sfærisk
• 3 eksempler
  • 3.1 Eksempel 1
  • 3.2 Eksempel 2
• 4 Øvelser
  • 4.1 Øvelse 1
  • 4.2 Øvelse 2
• 5 Referencer

Ændring af koordinater

Formlerne, der tillader opnåelse af de kartesiske koordinater (x, y, z) for et punkt M, gives nedenfor, forudsat at de sfæriske koordinater for det samme (r, θ, φ) punkt er kendte:

x = r Sen (θ) Cos (φ)

y = r Sen (θ) Sen (φ) 

z = r Cos (θ)

På samme måde er det nyttigt at finde relationerne til at gå fra de kartesiske koordinater (x, y, z) for et givet punkt til de sfæriske koordinater for det nævnte punkt:

r = √ (x ^ 2 + y ^ 2 + z ^ 2)

θ = Arctan (√ (x ^ 2 + y ^ 2) / z)

φ = Arctan (y / x)

Vektorbase i sfæriske koordinater

Fra de sfæriske koordinater defineres et ortonormalt basis af basisvektorer, der betegnes med Ur, Uθ, Uφ. Figur 1 viser disse tre enhedsvektorer, der har følgende egenskaber:

- Ur er enhedsvektoren tangent til den radiale linje θ = ctte og φ = ctte;

- Uθ er enhedsvektoren tangent til buen φ = ctte og r = ctte;

- Uφ er enhedsvektoren tangent til buen r = ctte og θ = ctte.

Linje- og volumenelementer i sfæriske koordinater

Positionsvektoren for et punkt i rummet i sfæriske koordinater er skrevet således:

r = r Ur

Men en uendelig minimal variation eller forskydning af et punkt i et tredimensionelt rum, i disse koordinater, udtrykkes ved følgende vektorrelation:

dr = dr Ur + r dθ Uθ + r Sen (θ) dφ Uφ

Endelig skrives et uendeligt stort volumen dV i sfæriske koordinater således:

dV = r ^ 2 Sen (θ) dr dθ dφ

Disse forhold er meget nyttige til beregning af linje- og volumenintegraler i fysiske situationer, der har sfærisk symmetri..

Forholdet til geografiske koordinater

Med geografiske koordinater forstås de, der tjener til at lokalisere steder på jordens overflade. Dette system bruger koordinaterne for bredde og længdegrad til at lokalisere positionen på jordens overflade..

I det geografiske koordinatsystem antages jordoverfladen at være sfærisk med radius Rt, selvom det vides at være fladt ved polerne, og et sæt imaginære linjer kaldet paralleller og meridianer betragtes.

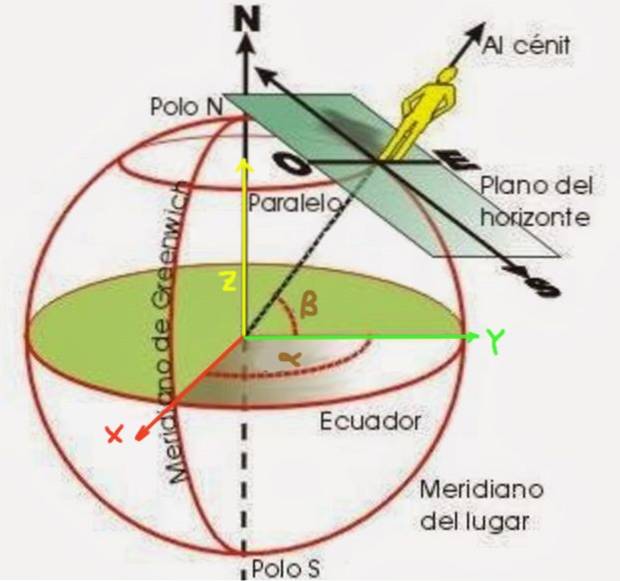
Breddegraden β er en vinkel dannet af en radius, der starter fra midten af ​​jorden til det punkt, du vil placere. Det måles fra ækvatorplanet, som vist i figur 2. På den anden side er længdegraden α den vinkel, som meridianen af ​​det punkt, der er placeret, danner i forhold til nulmeridianen (kendt som Greenwich-meridianen).

Breddegraden kan være nordlig eller sydlig, afhængigt af om det sted, du finder, er på den nordlige halvkugle eller på den sydlige halvkugle. Tilsvarende kan længdegraden være vest eller øst afhængigt af om placeringen er vest eller øst for nulmeridianen..

Formler til at skifte fra geografisk til sfærisk

For at opnå disse formler er den første ting at etablere et koordinatsystem. XY-planet vælges til at falde sammen med ækvatorialplanet, hvor den positive X-halvakse er den, der går fra midten af ​​jorden og passerer gennem nulmeridianen. Til gengæld passerer Y-aksen gennem meridianen 90º E. Jordoverfladen har en radius Rt.

Med dette koordinatsystem ser transformationerne fra geografisk til sfærisk sådan ud:

αEβN → (Rt, θ = 90º-β, φ = α)

αOβN → (Rt, θ = 90º-β, φ = 360º-α)

αEβS → (Rt, θ = 90º + β, φ = α)

αOβS → (Rt, θ = 90º + β, φ = 360º-α) 

Eksempler

Eksempel 1

De geografiske koordinater for Palma de Mallorca (Spanien) er:

Østlængdegrad 38.847º og nordlig bredde 39.570º. For at bestemme de sfæriske koordinater, der svarer til Palma de Mallorca, anvendes den første af formlerne for formlerne i det foregående afsnit:

38.847ºE39.570ºN → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)

Så de sfæriske koordinater er:

Palma de Mallorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)

I det forrige svar har vi taget r lig med jordens gennemsnitlige radius.

Eksempel 2

Ved at vide, at Falklandsøerne (Malvinas) har geografiske koordinater på 59ºO 51,75ºS, skal du bestemme de tilsvarende polære koordinater. Husk, at X-aksen går fra midten af ​​jorden til 0º-meridianen og på ækvatorialplanet; Y-aksen også i ækvatorialplanet og passerer gennem 90 ° vestmeridianen; endelig Z-aksen på Jordens rotationsakse i retning Syd-Nord.

For at finde de tilsvarende sfæriske koordinater bruger vi formlerne præsenteret i det foregående afsnit:

59ºO 51,75ºS → (r = 6371 km, θ = 90º + 51,75º, φ = 360º-59º) det vil sige

Falklandsøerne: (r = 6371 km, θ = 141.75º, φ = 301º)

Uddannelse

Øvelse 1

Find de kartesiske koordinater for Palma de Mallorca i XYZ kartesiske referencesystem vist i figur 2.

Opløsning: Tidligere blev der i eksempel 1 opnået de sfæriske koordinater startende fra de geografiske koordinater i Palma de Mallorca. Så formlerne præsenteret ovenfor kan bruges til at gå fra sfærisk til kartesisk:

x = 6371 km Sen (50.43º) Cos (38.85º)

y = 6371 km Sen (50.43º) Sen (38.85º) 

z = 6371 km Cos (50,43º)

Udførelse af de tilsvarende beregninger, vi har:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Øvelse 2

Find de kartesiske koordinater for Falklandsøerne i XYZ kartesiske referencesystem vist i figur 2.

Opløsning: Tidligere, i eksempel 2, blev de sfæriske koordinater opnået startende fra de geografiske koordinater for Falklandsøerne. Så formlerne præsenteret ovenfor kan bruges til at gå fra sfærisk til kartesisk:

x = 6371 km Sen (141,75º) Cos (301º)

y = 6371 km Sen (141,75º) Sen (301º) 

z = 6371 km Cos (141,75º)

Ved at udføre de tilsvarende beregninger opnår vi:

Falklandsøerne: (x = 2031 km, y = -3381 km, z = -5003)

Referencer

1. Arfken G og Weber H. (2012). Matematiske metoder til fysikere. En omfattende guide. 7. udgave. Akademisk presse. ISBN 978-0-12-384654-9
2. Beregning cc. Løste problemer med cylindriske og sfæriske koordinater. Gendannet fra: calculo.cc
3. Astronomi workshop. Breddegrad og længdegrad. Gendannet fra: tarifamates.blogspot.com/
4. Weisstein, Eric W. "Sfæriske koordinater." Fra MathWorld-A Wolfram Web. Gendannet fra: mathworld.wolfram.com
5. wikipedia. Sfærisk koordinatsystem. Gendannet fra: en.wikipedia.com
6. wikipedia. Vektorfelter i cylindriske og sfæriske koordinater. Gendannet fra: en.wikipedia.com