Hvad er funktionsperioden y = 3sen (4x)?

Det periode for funktionen y = 3sen (4x) er 2π / 4 = π / 2. For klart at forstå årsagen til denne erklæring, skal definitionen af ​​en funktions periode og funktionsperioden sin (x) være kendt; lidt om tegning af funktioner vil også være nyttigt.

Trigonometriske funktioner, såsom sinus og cosinus (sin (x) og cos (x)), er meget nyttige i både matematik og teknik.

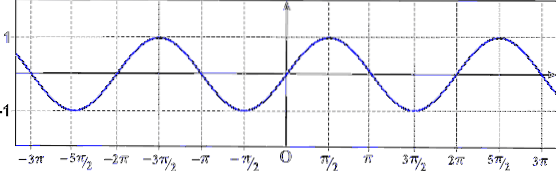
Ordet periode henviser til gentagelsen af ​​en begivenhed, så at sige, at en funktion er periodisk svarer til at sige "dens graf er gentagelsen af ​​et stykke kurve." Som det kan ses i det foregående billede, er funktionen sin (x) periodisk.

Periodiske funktioner

En funktion f (x) siges at være periodisk, hvis der findes en reel værdi p ≠ 0, således at f (x + p) = f (x) for alle x i funktionens domæne. I dette tilfælde er funktionsperioden p.

Funktionens periode kaldes generelt det mindste positive reelle tal p, der opfylder definitionen.

Som det kan ses i den forrige graf, er funktionen sin (x) periodisk, og dens periode er 2π (cosinusfunktionen er også periodisk med en periode lig med 2π).

Ændringer i grafen for en funktion

Lad f (x) være en funktion, hvis graf er kendt, og lad c være en positiv konstant. Hvad sker der med grafen for f (x), hvis f (x) ganges med c? Med andre ord, hvad er grafen for c * f (x) og f (cx)?

Graf for c * f (x)

Når en funktion multipliceres eksternt med en positiv konstant, gennemgår grafen for f (x) en udgang i outputværdierne; ændringen er lodret, og der er to tilfælde:

- Hvis c> 1, gennemgår grafen en lodret strækning med faktoren c.

- Ja 0

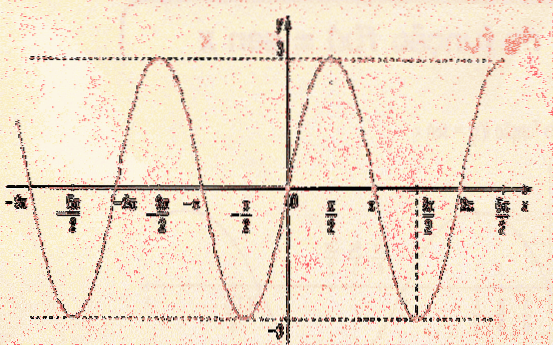
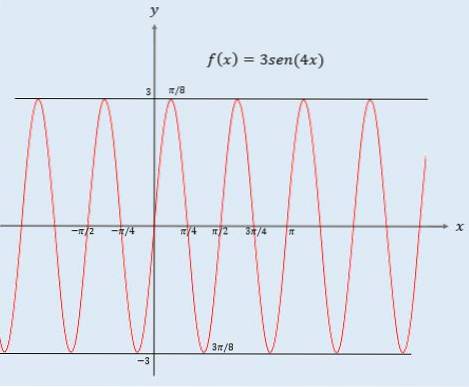
Graf for f (cx)

Når argumentet for en funktion ganges med en konstant, gennemgår grafen for f (x) en ændring af inputværdierne; ændringen er vandret, og som før kan der være to tilfælde:

- Hvis c> 1, gennemgår grafen vandret kompression med en faktor 1 / c.

- Ja 0

Funktionsperiode y = 3sen (4x)

Det skal bemærkes, at der i funktionen f (x) = 3sen (4x) er to konstanter, der ændrer grafen for sinusfunktionen: en ganges eksternt og den anden internt..

3, der er uden for sinusfunktionen, hvad den gør, forlænger funktionen lodret med en faktor 3. Dette indebærer, at grafen for funktion 3 sin (x) vil være mellem værdierne -3 og 3.

4 inden i sinusfunktionen får grafen til funktionen til at gennemgå vandret kompression med en faktor på 1/4.

På den anden side måles en funktionsperiode vandret. Da funktionsperioden sin (x) er 2π, vil i betragtning af sin (4x) periodens størrelse ændre sig.

For at finde ud af, hvad perioden af ​​y = 3sen (4x) er, skal du blot gange perioden for funktionen sin (x) med 1/4 (kompressionsfaktoren).

Med andre ord er funktionsperioden y = 3sin (4x) 2π / 4 = π / 2, som det kan ses i den sidste graf.

Referencer

1. Fleming, W., & Varberg, D. E. (1989). Præcalculus matematik. Prentice Hall PTR.
2. Fleming, W., & Varberg, D. E. (1989). Precalculus matematik: en problemløsningstilgang (2, Illustreret udgave). Michigan: Prentice Hall.
3. Larson, R. (2010). Precalculus (8. udgave). Cengage læring.
4. Pérez, C. D. (2006). Forberegning. Pearson Uddannelse.
5. Purcell, E. J., Varberg, D. og Rigdon, S. E. (2007). Beregning (9. udgave). Prentice hall.
6. Saenz, J. (2005). Differentiel beregning med tidlige transcendente funktioner til videnskab og teknik (Anden udgave udgave). Hypotenus.
7. Sullivan, M. (1997). Forberegning. Pearson Uddannelse.