Det vægtlove for kemi Det er dem, der har vist, at masserne af de stoffer, der reagerer, ikke gør det vilkårligt eller tilfældigt; men ved at opretholde en konstant matematisk andel af heltal eller submultipler deraf, hvor elementernes atomer hverken er skabt eller ødelagt.
Tidligere har det været nødvendigt at etablere disse love ekstraordinære argumenter; for skønt det synes for indlysende nu, før atom- eller molekylmasserne af henholdsvis elementerne eller forbindelserne ikke engang var kendt.
Da det ikke vides nøjagtigt, hvor meget en mol atomer af hvert element svarede til, måtte kemikere i det 18. og 19. århundrede stole på de reagerende masser. Så rudimentære analytiske balancer (øverste billede) var uadskillelige ledsagere i løbet af de hundreder af eksperimenter, der kræves for at etablere vægtloven..
Det er af denne grund, at når du studerer disse kemilove, støder du på massemålinger i hvert øjeblik. Takket være dette, ekstrapolering af resultaterne af eksperimenterne, blev det opdaget, at de kemiske forbindelser cigarer er altid dannet med den samme masseandel af deres bestanddele.
Artikelindeks
Denne lov siger, at i en kemisk reaktion er den samlede masse af reaktanterne lig med den samlede masse af produkterne; så længe det betragtede system er lukket, og der ikke er nogen udveksling af masse og energi med omgivelserne.
I en kemisk reaktion forsvinder stoffer ikke, men omdannes til andre stoffer med samme masse; deraf den berømte sætning: "intet er skabt, intet ødelægges, alt er transformeret".
Historisk blev loven om bevarelse af masse i en kemisk reaktion først foreslået i 1756 af Mikhail Lomonsov, der viste resultaterne af sine eksperimenter i sin journal..
Senere i 1774 præsenterede fransk kemiker Antoine Levoisier resultaterne af sine eksperimenter, der gjorde det muligt at fastslå dette; som nogle også kalder det Lavoisiers lov.
På Lavoisiers tid (1743-1794) var der Phlogiston-teorien, ifølge hvilken kroppe havde evnen til at antænde eller brænde. Lavoisiers eksperimenter gjorde det muligt at kassere denne teori.
Lavoisier gennemførte adskillige metalforbrændingseksperimenter. Han vejede omhyggeligt materialerne før og efter forbrændingen i en lukket beholder og fandt ud af, at der var en tilsyneladende vægtforøgelse..
Men Lavoiser, baseret på sin viden om iltens rolle i forbrændingen, konkluderede, at vægtforøgelsen ved forbrænding skyldtes inkorporering af ilt i det brændende materiale. Begrebet metaloxider blev født.
Derfor forblev summen af masserne af metaller, der blev udsat for forbrænding, og ilt uændret. Denne konklusion tillod oprettelsen af loven om bevarelse af masse.
Loven om konservering af masser fastslog behovet for at afbalancere kemiske ligninger og garanterede, at antallet af alle de grundstoffer, der deltager i en kemisk reaktion, både som reaktanter eller som produkter, er nøjagtigt det samme..
Dette er et væsentligt krav for nøjagtigheden af de støkiometriske beregninger, der skal udføres..
Hvor mange mol vand kan der produceres under forbrændingen af 5 mol methan i overskydende ilt? Vis også, at loven om bevarelse af materie er opfyldt..
CH4 + 2 Oto => COto + 2 timertoELLER
Når man observerer den afbalancerede ligning af reaktionen, konkluderes det, at 1 mol methan producerer 2 mol vand.
Problemet kan løses direkte med en enkel tilgang, da vi ikke har 1 mol, men 5 mol CH4:
Mol vand = 5 mol CH4(2 mol HtoO / 1 mol CH4)
= 10
Hvilket svarer til 180 g HtoO. Også dannet 5 mol eller 220 g COto, hvilket er lig med en samlet masse på 400 g produkter.
For at loven om konservering af stof skal være opfyldt, skal 400 g reagenser reagere; ikke mere ikke mindre. Af disse 400 g svarer 80 g til 5 mol CH4 (multipliceret med dens molekylvægt på 16 g / mol) og 320 g ved 10 mol Oto (på samme måde for dens molekylvægt på 32 g / mol).
Et 1,50 g magnesiumbånd blev brændt i en lukket beholder indeholdende 0,80 g ilt. Efter forbrænding forblev 0,25 g ilt i beholderen. a) Hvilken iltmasse reagerede? b) Hvor meget magnesiumoxid der blev dannet?
Massen af ilt, der reagerede, opnås ved en simpel forskel.
Forbrugt iltmasse = (startmasse - restmasse) ilt
= 0,80 g - 0,25 g
= 0,55 g Oto (til)
I henhold til loven om bevarelse af masse,
Masse af magnesiumoxid = masse af magnesium + masse af ilt
= 1,50 g + 0,55 g
= 2,05 g MgO (b)
Joseph Louis Proust (1754-1826), fransk kemiker, indså, at i en kemisk reaktion reagerer de kemiske grundstoffer altid i faste proportioner af masser for at danne en forbindelse ren bestemt; derfor er dens sammensætning konstant, uanset kilde eller oprindelse, eller hvordan den syntetiseres.
Proust erklærede i 1799 loven med bestemte proportioner, der siger, at: "Når to eller flere grundstoffer kombineres for at danne en forbindelse, gør de det i et fast masseforhold." Derefter er dette forhold fast og afhænger ikke af den strategi, der følges til fremstilling af forbindelsen..
Denne lov er også kendt som loven om konstant sammensætning, der siger, at: "Enhver kemisk forbindelse i en renhedstilstand indeholder altid de samme grundstoffer i en konstant andel af massen.".
Jern (Fe) reagerer med svovl (S) for at danne jernsulfid (FeS), tre situationer kan bemærkes (1, 2 og 3):
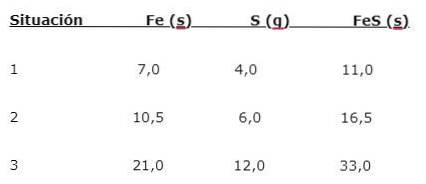
For at finde den andel, hvor elementerne kombineres, skal du dele den større masse (Fe) med den mindre masse (S). Beregningen giver et forhold på 1,75: 1. Denne værdi gentages under de tre angivne betingelser (1, 2 og 3), hvor den samme andel opnås, selvom der anvendes forskellige masser..
Det vil sige 1,75 g Fe kombineres med 1,0 g S for at give 2,75 g FeS.
Ved at anvende denne lov er det muligt at kende nøjagtigt masserne af de grundstoffer, der skal kombineres for at opnå en ønsket masse af en forbindelse..
På denne måde kan der opnås information om den overskydende masse af ethvert af elementerne, der er involveret i en kemisk reaktion, eller hvis der er et begrænsende reagens i reaktionen..
Derudover anvendes det til at kende den centesimale sammensætning af en forbindelse, og baseret på sidstnævnte kan formlen for en forbindelse etableres.
Kuldioxid (COto) dannes i følgende reaktion:
C + Oto => COto
12 g kulstof kombinerer 32 g ilt for at give 44 g kuldioxid.
Så procenten kulstof er lig
Kulstofprocent = (12 g / 44 g) 100%
= 27,3%
Oxygenprocent = (32 g / 44 g) 100%
Procent af ilt = 72,7%
Ved hjælp af erklæringen fra loven om konstant sammensætning kan det bemærkes, at kuldioxid altid består af 27,3% kulstof og 72,7% ilt.
Når 4 g og 6 g svovl (S) blev omsat med ilt (O) i forskellige beholdere, blev 10 g og 15 g svovltrioxid (SO3).
Hvorfor blev der opnået sådanne mængder svovltrioxid og ikke andre?
Beregn også den mængde svovl, der kræves for at kombinere med 36 g ilt og den opnåede masse af svovletrioxid.
I den første beholder blandes 4 svovl med X g ilt for at opnå 10 g trioxid. Hvis loven om bevarelse af masse anvendes, kan vi løse den iltmasse, der kombineres med svovlet.
Masse af ilt = 10 g ilttrioxid - 4 g svovl.
= 6 g
I beholder 2 blandes 6 g svovl med X g ilt til opnåelse af 15 svovltrioxid.
Masse af ilt = 15 g svovltrioxid - 6 g svovl
= 9 g
Vi fortsætter derefter med at beregne O / S-forholdet for hver container:
O / S-forhold i situation 1 = 6 g O / 4 g S
= 1,5 / 1
O / S-forhold i situation 2 = 9 g O / 6 g S
= 1,5 / 1
Hvilket er i overensstemmelse med det, der er angivet i loven med definerede proportioner, hvilket indikerer, at elementerne altid kombineres i samme forhold for at danne en bestemt forbindelse..
Derfor er de opnåede værdier korrekte og dem, der svarer til anvendelsen af loven.
I det foregående afsnit blev en værdi på 1,5 / 1 beregnet for O / S-forholdet.
g svovl = 36 ilt (1 g svovl / 1,5 g ilt)
= 24 g
g svovltrioxid = 36 g ilt + 24 g svovl
= 60 g
Klor og magnesium kombineres i forholdet 2,95 g klor for hver g magnesium. a) Bestem de masser af klor og magnesium, der er nødvendige for at opnå 25 g magnesiumchlorid. b) Hvad er den procentvise sammensætning af magnesiumchlorid?
Baseret på værdien 2,95 for Cl: Mg-forholdet kan følgende fremgangsmåde foretages:
2,95 g Cl + 1 g Mg => 3,95 g MgClto
Senere:
g Cl = 25 g MgClto (2,95 g Cl / 3,95 g MgClto)
= 18,67
g Mg = 25 g MgClto (1 g Mg / 3,95 g MgClto)
= 6,33
Så 18,67 g chlor kombineres med 6,33 g magnesium for at producere 25 g magnesiumchlorid..
Beregn først molekylvægten af magnesiumchlorid, MgClto:
Molekylvægt MgClto = 24,3 g / mol + (2 35,5 g / mol)
= 95,3 g / mol
Magnesiumprocent = (24,3 g / 95,3 g) x 100%
= 25,5%
Klorprocent = (71 g / 95,3 g) x 100%
= 74,5%
Loven blev udtalt i 1803 af den franske kemiker og meteorolog John Dalton, baseret på hans observationer vedrørende reaktionerne fra atmosfæriske gasser.
Loven blev udtalt på følgende måde: "Når elementer kombineres til at give mere end en forbindelse, forbinder en variabel masse af den ene af dem med en fast masse af den anden, og den første har som et forhold mellem kanoniske og utydelige tal".
Også: "Når to elementer kombineres for at stamme fra forskellige forbindelser, givet en fast mængde af en af dem, er de forskellige mængder af det andet element, der kombineres med den faste mængde for at producere forbindelserne, i forhold til enkle heltal".
John Dalton lavede den første moderne beskrivelse af atomet som en komponent i de kemiske grundstoffer, da han påpegede, at grundstofferne består af udelelige partikler kaldet atomer..
Derudover postulerede han, at forbindelser dannes, når atomer med forskellige grundstoffer kombineres med hinanden i enkle heltal..
Dalton afsluttede Prousts efterforskningsværker. Han påpegede eksistensen af to tinoxider med procentdele på 88,1% og 78,7% tin med de tilsvarende procentdele af ilt, henholdsvis 11,9% og 21,3%..
Vis, at forbindelserne vand, HtoO og hydrogenperoxid, HtoELLERto, overholde loven om flere forhold.
Elementernes atomvægt: H = 1 g / mol og ilt = 16 g / mol.
Molekylvægte af forbindelser: HtoO = 18 g / mol og HtoELLERto = 34 g / mol.
Brint er elementet med en fast mængde i HtoO og HtoELLERto, så forholdene mellem O og H i begge forbindelser vil blive etableret.
O / H-forhold i HtoO = (16 g / mol) / (2 g / mol)
= 8/1
O / H-forhold i HtoELLERto = (32 g / mol) / (2 g / mol)
= 16/1
Forholdet mellem begge proportioner = (16/1) / (8/1)
= 2
Så O / H-forholdet mellem hydrogenperoxid og vand er 2, et simpelt heltal. Derfor demonstreres overholdelse af loven om flere forhold..
Hvilken iltmasse kombineres med 3,0 g kvælstof i a) nitrogenoxid, NO og b) nitrogendioxid, NOto. Vis, at NEJ og NEJto overholde loven om flere forhold.
Masse af nitrogen = 3 g
Atomvægte: nitrogen, 14 g / mol og ilt, 16 g / mol.
I NO kombineres et N-atom med 1 O-atom, så iltmassen, der kombineres med 3 g nitrogen, kan beregnes ved hjælp af følgende tilgang:
g O = g nitrogen · (PA. O / PA. N)
= 3 g (16 g / mol / 14 g / mol)
= 3,43 g O
I NEJto, et N-atom kombineres med 2 O-atomer, så massen af ilt, der kombineres, er:
g ilt = 3 g (32 g / mol / 14 g / mol)
= 6,86 g O
O / N-forhold i NO = 3,43 g O / 3 g N
= 1.143
O / N-forhold i NOto = 6,86 g O / 3 g N
= 2.282
Værdien af forholdet mellem O / N-forholdene = 2.282 / 1.143
= 2
Så værdien af O / N-forholdet er 2, et simpelt heltal. Derfor er loven om flere forhold opfyldt..
Denne lov, der er formuleret af Richter og Carl F. Wenzel hver for sig, fastslår, at masseforholdene for to forbindelser med et element til fælles tillader at bestemme andelen af en tredje forbindelse blandt de andre grundstoffer, hvis de reagerer.
For eksempel, hvis du har de to forbindelser AB og CB, kan du se, at det fælles element er B.
Richter-Wenzel-loven eller loven om gensidige proportioner siger, at når vi ved, hvor meget af A der reagerer med B for at give AB, og hvor meget af C reagerer med B for at give CB, kan vi beregne den masse af A, der er nødvendig for at reagere med en masse af C til dannelse af AC.
Og resultatet er, at forholdet A: C eller A / C skal være et multiplum eller submultipel af A / B eller C / B. Imidlertid er denne lov ikke altid opfyldt, især når elementerne præsenterer forskellige oxidationstilstande..
Af alle de underlige love er dette måske den mest "abstrakte" eller komplicerede. Men hvis det analyseres fra et matematisk synspunkt, vil det ses, at det kun består af konverteringsfaktorer og aflysninger.
Hvis det vides, at 12 g kulstof reagerer med 32 g ilt til dannelse af kuldioxid; og at derimod 2 g hydrogen reagerer med 16 g ilt til dannelse af vand, så kan masseforholdene C / O og H / O for CO estimeresto og HtoEller henholdsvis.
Beregning af C / O og H / O har vi:
C / O = 12 g C / 32 g O
= 3/8
H / O = 2 g H / 16 g O
= 1/8
Oxygen er det fælles element, og du vil vide, hvor meget kulstof der reagerer med brint for at producere metan; det vil sige, at du vil beregne C / H (eller H / C). Derefter er det nødvendigt at foretage en opdeling af de tidligere proportioner for at vise, om gensidighed er opfyldt eller ej:
C / H = (C / O) / (H / O)
Bemærk at på denne måde annulleres O'erne, og C / H forbliver:
C / H = (3/8) / (1/8)
= 3
Og 3 er et multiplum af 3/8 (3/8 x 8). Dette betyder, at 3 g C reagerer med 1 g H for at give methan. Men for at kunne sammenligne det med COto, gang C / H med 4, hvilket er lig med 12; dette giver 12 g C, der reagerer med 4 g H til dannelse af methan, hvilket også er sandt.
Hvis det vides, at 24 g magnesium reagerer med 2 g hydrogen til dannelse af magnesiumhydrid; og at derudover reagerer 32 g svovl med 2 g hydrogen til dannelse af hydrogensulfid, elementet til fælles er hydrogen, og vi vil beregne Mg / S ud fra Mg / H og H / S.
Derefter beregner vi Mg / H og H / S separat, vi har:
Mg / H = 24 g Mg / 2 g H
= 12
H / S = 2 g H / 32 g S
= 1/16
Det er dog praktisk at bruge S / H til at annullere H. Derfor er S / H lig med 16. Når dette er gjort, fortsætter vi med at beregne Mg / S:
Mg / S = (Mg / H) / (S / H)
= (12/16)
= 3/4
Og 3/4 er en delmultipel på 12 (3/4 x 16). Mg / S-forholdet indikerer, at 3 g Mg reagerer med 4 g svovl til dannelse af magnesiumsulfid. Du skal dog multiplicere Mg / S med 8 for at kunne sammenligne det med Mg / H. Således reagerer 24 g Mg med 32 g svovl for at give dette metallsulfid.
Det er kendt, at 35,5 g Cl reagerer med 1 g H til dannelse af HCI. Ligeledes reagerer 27 g Al med 3 g H til dannelse af AlH3. Beregn andelen af aluminiumchlorid, og fortæl, om en sådan forbindelse overholder Richter-Wenzel-loven.
Igen fortsætter vi med at beregne Cl / H og Al / H separat:
Cl / H = 35,5 g Cl / 1 g H
= 35,5
Al / H = 27 g Al / 3 g H
= 9
Nu beregnes Al / Cl:
Al / Cl = (Al / H) / (Cl / H)
= 9 / 35,5
≈ 0.250 eller 1/4 (faktisk 0.253)
Det vil sige, at 0,250 g Al reagerer med 1 g Cl til dannelse af det tilsvarende salt. Men igen skal Al / Cl ganges med et tal, der gør det muligt at sammenligne det (for nemheds skyld) med Al / H.
Al / Cl ganges derefter med 108 (27 / 0.250), hvilket giver 27 g Al, der reagerer med 108 g Cl. Dette er ikke nøjagtigt tilfældet. Hvis vi f.eks. Tager værdien 0,253 gange Al / Cl og multiplicerer den med 106,7 (27 / 0,253), vil vi have, at 27 g Al reagerer med 106,7 g Cl; som er tættere på virkeligheden (AlCl3, med en PA på 35,5 g / mol for Cl).
Her er hvordan Richters lov kan begynde at svække på grund af præcision og misbrug af decimaler..
Endnu ingen kommentarer