Hvad er delene af det kartesiske fly?

Det dele af det kartesiske plan De er sammensat af to rigtige linjer, vinkelret, som deler det kartesiske plan i fire regioner. Hver af disse regioner kaldes kvadranter, og elementerne i det kartesiske plan kaldes punkter. Flyet kaldes sammen med koordinatakserne Cartesian fly til ære for den franske filosof René Descartes, der opfandt analytisk geometri.

De to linjer (eller koordinatakser) er vinkelrette, fordi de danner en vinkel på 90 ° mellem dem, og de skærer hinanden ved et fælles punkt (oprindelse). En af linjerne er vandret, kaldes oprindelsen til x (eller abscissa) og den anden linje er lodret, kaldes oprindelsen til y (eller ordinat).

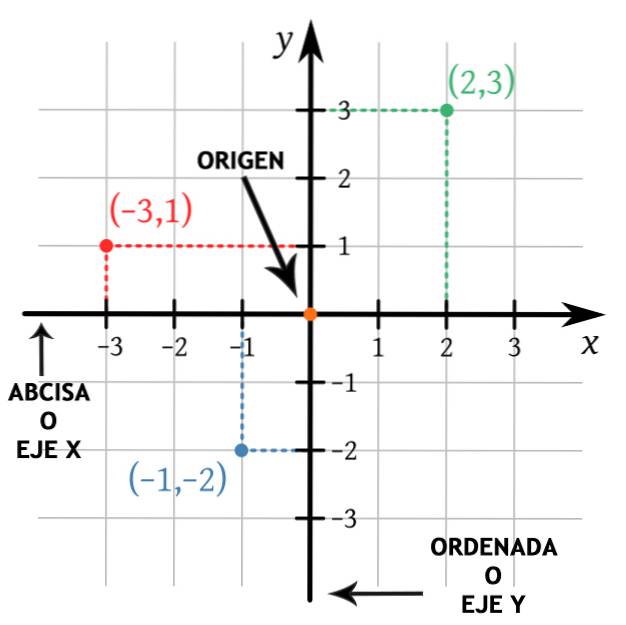
Den positive halvdel af X-aksen er til højre for oprindelsen, og den positive halvdel af Y-aksen er op fra oprindelsen. Dette gør det muligt at skelne mellem de fire kvadranter i det kartesiske plan, hvilket er meget nyttigt, når man plotter punkter i planet..

Punkter på det kartesiske plan

På hvert punkt P flyet kan tildeles et par reelle tal, der er dets kartesiske koordinater.

Hvis en vandret linje og en lodret linje passerer igennem P, og disse skærer X-aksen og Y-aksen ved punkterne til Y b henholdsvis derefter koordinaterne for P De er (til,b). Det kaldes (til,b) et ordnet par og rækkefølgen, hvor tallene skrives, er vigtig.

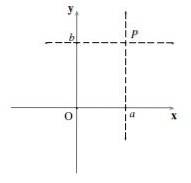
Det første nummer, til, er koordinaten i "x" (eller abscissa) og det andet tal, b, er y-koordinaten (eller ordinaten). Notationen bruges P = (til,b).

Det fremgår tydeligt af den måde, hvorpå det kartesiske plan blev konstrueret, at oprindelsen svarer til koordinaterne 0 på "x" -aksen og 0 på "y" -aksen, dvs., ELLER= (0,0).

Kvadranter af det kartesiske plan

Som det kan ses i de foregående figurer, genererer koordinatakserne fire forskellige regioner, der er kvadranterne for det kartesiske plan, som er angivet med bogstaverne I, II, III Y IV og disse adskiller sig fra hinanden i det tegn, som de punkter, der findes i hver af dem.

Kvadrant jeg

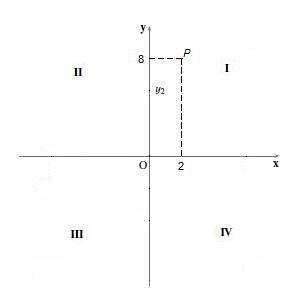
Kvadrantens punkter jeg er dem, der har begge koordinater med et positivt tegn, dvs. deres x-koordinat og y-koordinat er positive.

For eksempel pointen P = (2,8). For at tegne det er punkt 2 placeret på "x" -aksen og punkt 8 på "y" -aksen, hvorefter de lodrette og vandrette linjer trækkes henholdsvis, og hvor de skærer hinanden, er hvor punktet er. P.

Kvadrant II

Kvadrantens punkter II de har en negativ "x" -koordinat og en positiv "y" -koordinat. For eksempel pointen Q = (- 4,5). Det er tegnet som i det foregående tilfælde.

Kvadrant III

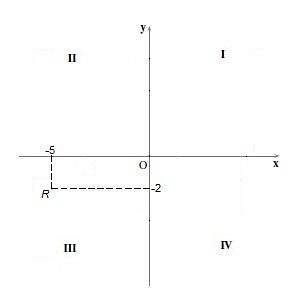
I denne kvadrant er begge koordinaters tegn negativt, det vil sige "x" -koordinaten og "y" -koordinaten er negativ. For eksempel er punktet R = (- 5, -2).

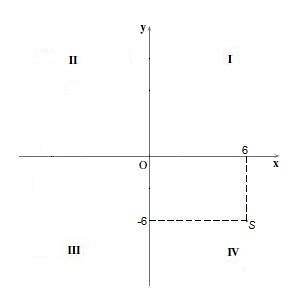
Kvadrant IV

I kvadranten IV punkterne har en positiv "x" -koordinat og en negativ "y" -koordinat. For eksempel pointen S = (6, -6).

Referencer

1. Fleming, W., & Varberg, D. (1991). Algebra og trigonometri med analytisk geometri. Pearson Uddannelse.
2. Larson, R. (2010). Precalculus (8. udgave). Cengage læring.
3. Leal, J. M., og Viloria, N. G. (2005). Flyanalytisk geometri. Mérida - Venezuela: Redaktionel Venezolana C. A.
4. Oteyza, E. (2005). Analytisk geometri (Anden udgave). (G. T. Mendoza, red.) Pearson Education.
5. Oteyza, E. d., Osnaya, E. L., Garciadiego, C. H., Hoyo, A. M., & Flores, A. R. (2001). Analytisk geometri og trigonometri (Første udgave). Pearson Uddannelse.
6. Purcell, E. J., Varberg, D. og Rigdon, S. E. (2007). Beregning (9. udgave). Prentice hall.
7. Scott, C. A. (2009). Cartesian Plane Geometry, Part: Analytical Conics (1907) (genudskrivning red.). Lynkilde.