
Hvad er forskellen mellem sti og forskydning?
Det hovedforskel mellem bane og forskydning er, at sidstnævnte er afstanden og retningen, som en genstand har rejst, mens førstnævnte er den sti eller form, som objektets bevægelse tager.
For at se mere tydeligt forskellene mellem forskydning og bane er det imidlertid bedre at specificere dens konceptualisering gennem eksempler, der giver en bedre forståelse af begge termer..
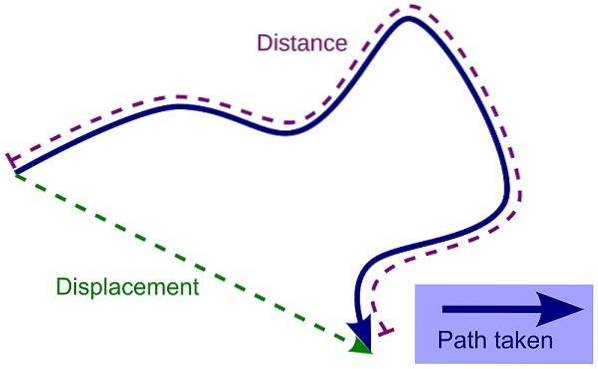
Forskydning
Det forstås som afstanden og retningen, som en genstand rejser under hensyntagen til dens oprindelige position og dens endelige position, altid i en lige linje. Da det er en vektorstørrelse, bruges målingerne af længden kendt som centimeter, meter eller kilometer..
Formlen til beregning af forskydningen er defineret som følger:
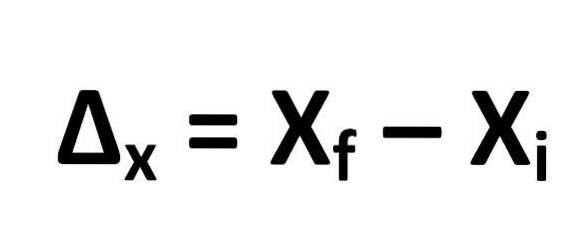
Heraf følger, at:
- Δx = forskydning
- xF = objektets endelige position
- xjeg = objektets startposition
Eksempel på forskydning
1- Hvis en gruppe børn er ved begyndelsen af en rute, hvis startposition er 50 m, bevæger sig i en lige linje, skal du bestemme forskydningen ved hvert af punkterne XF .
- xF = 120m
- xF = 90m
- xF = 60m
- xF = 40m
2- Problemets data ekstraheres ved at erstatte værdierne på Xto og X1 i forskydningsformlen:
- Δx = ?
- xjeg = 50m
- Δx = XF - xjeg
- Δx = 120m - 50m = 70m
3- I denne første tilgang siger vi, at Δx er lig med 120m, hvilket svarer til den første værdi, vi finder på XF, minus 50m, som er værdien af Xjeg, Resultatet er 70m, det vil sige, når forskydningen var 120m, var forskydningen 70m til højre.
4- Vi fortsætter med at løse på samme måde værdierne for b, c og d
- Δx = 90m - 50m = 40m
- Δx = 60m - 50m = 10m
- Δx = 40m - 50m = - 10m
I dette tilfælde gav forskydningen os negativ, det betyder, at den endelige position er i den modsatte retning af den oprindelige position.
Bane
Det er den rute eller linje, der bestemmes af et objekt under dets bevægelse, og dets evaluering i det internationale system, antager generelt geometriske former som linjen, parabolen, cirklen eller ellipsen). Det identificeres gennem en imaginær linje, og fordi det er en skalar størrelse, måles den i meter.
Det skal bemærkes, at for at beregne banen skal vi vide, om kroppen er i ro eller bevægelse, dvs. den udsættes for det referencesystem, som vi vælger.
Ligningen til beregning af et objekts bane i det internationale system er givet ved:
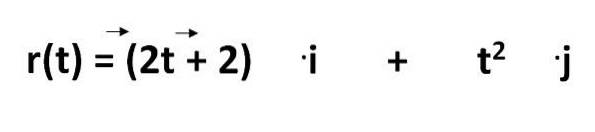
Heraf skal vi:
- r (t) = er ligningen af stien
- 2t - 2 og tto = repræsenterer koordinater som en funktion af tiden
- .jeg og .j = er enhedsvektorerne
For at forstå beregningen af den sti, som et objekt har rejst, skal vi udvikle følgende eksempel:
- Beregn ligningen af banerne for følgende positionsvektorer:
- r (t) = (2t + 7) .jeg + tto .j
- r (t) = (t - 2) .jeg + 2t .j
Første trin: Da en sti ligning er en funktion af X, defineres værdierne for henholdsvis X og Y i hver af de foreslåede vektorer for at gøre dette:
1- Løs den første positionsvektor:
- r (t) = (2t + 7) .jeg + tto .j
2- Ty = f (x), hvor X er givet af indholdet af enhedsvektoren .i og Y er angivet af indholdet af enhedsvektoren .j:
- X = 2t + 7
- Y = tto
3- y = f (x), dvs. tid er ikke en del af udtrykket, derfor skal vi løse det, vi har:
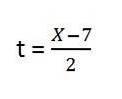
4- Vi erstatter clearingen i Y. Det forbliver:
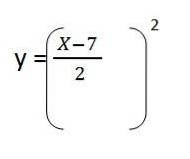
5- Vi løser indholdet af parenteserne, og vi har ligningen af den resulterende sti til den første enhedsvektor:
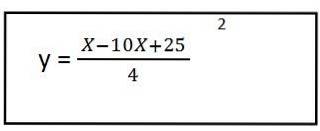
Som vi kan se, gav det os en andengrads ligning, det betyder, at banen har form af en parabel.
Andet trin: Vi fortsætter på samme måde til at beregne banen for den anden enhedsvektor
r (t) = (t - 2) .jeg + 2t .j
- X = t - 2
- Y = 2t
2- Efter at have fulgt de trin, vi tidligere har set y = f (x), skal vi rydde tiden, fordi det ikke er en del af udtrykket, vi har tilbage med:
- t = X + 2
3- Vi erstatter clearingen i Y, resterende:
- y = 2 (X + 2)
4- Løsning af parenteser har vi ligningen af den resulterende bane for den anden enhedsvektor:
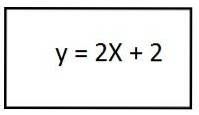
I denne procedure var resultatet en lige linje, som fortæller os, at banen har en retlinet form.
Når begreberne forskydning og bane er forstået, kan vi udlede resten af forskellene, der findes mellem begge termer.
Flere forskelle mellem forskydning og bane
Forskydning
- Det er afstanden og retningen, som en genstand rejser under hensyntagen til dens oprindelige position og dens endelige position.
- Det sker altid i en lige linje.
- Det genkendes med en pil.
- Brug længdemålinger (centimeter, meter, kilometer).
- Det er en vektormængde.
- Tag højde for retningen (til højre eller venstre)
- Den tager ikke højde for den tid, der er brugt under turen.
- Afhænger ikke af et referencesystem.
- Når startpunktet er det samme startpunkt, er forskydningen nul.
- Modulet skal falde sammen med pladsen til at rejse, så længe stien er en lige linje, og der er ingen ændringer i retningen, der skal følges.
- Modulet har en tendens til at stige eller falde, når bevægelsen sker, idet man tager i betragtning bane.
Bane
Det er den sti eller linje, der bestemmes af et objekt under dets bevægelse. Vedtager geometriske former (lige, parabolske, cirkulære eller elliptiske).
- Det er repræsenteret af en imaginær linje.
- Det måles i meter.
- Det er en skalær mængde.
- Det tager ikke højde for den kørte kørselsretning.
- Overvej tiden brugt under turen.
- Afhænger af et referencesystem.
- Når startpunktet eller startpositionen er den samme som den endelige position, angives banen af den tilbagelagte afstand.
- Banens værdi falder sammen med forskydningsvektorens modul, hvis den resulterende bane er en lige linje, men der ikke er nogen ændringer i retningen, der skal følges.
- Stiger altid, når kroppen bevæger sig, uanset bane.
Referencer
- Alvarado, N. (1972) Fysisk. Første videnskabsår. Redaktionel Fotoprin C.A. Venezuela.
- Fernández, M; Fidalgo, J. (2016). Fysik og kemi 1. Baccalaureat. Editions Paraninfo, S.A. Spanien.
- Guatemalas Institute of Radio Education. (2011) Grundlæggende fysik. Zaculeu Group første semester. Guatemala.
- Fernández, P. (2014) Videnskabelig-teknologisk felt. Paraninfo udgaver. S.A. Spanien.
- Fisica Lab (2015) Vector Displacement. Gendannet fra: fisicalab.com.
- Eksempler på. (2013) forskydning. Gendannet fra: examplesde.com.
- Living Room Home Project (2014) Hvad er forskydning? Gendannet fra: salonhogar.net.
- Fysiklaboratorium (2015) Begreb med bane og ligning af position. Gendannet fra: fisicalab.com.


Endnu ingen kommentarer