
Massefylde
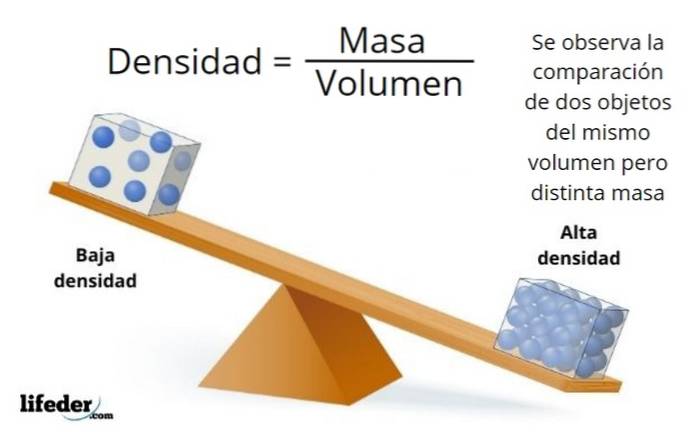
Hvad er densitet?
Det massefylde Massen af et stof er kvotienten mellem massen af prøven og det volumen, den optager, og dens måleenhed er kg / m3 i det internationale system for enheder. Det græske bogstav ρ (rho) bruges ofte til at betegne det.
Vandtætheden, som er den universelle væske, er 1000 kg / m3 eller 1 g / cm3 ved 25 ºC, da densiteten gennemgår ændringer med temperatur og tryk.
Mange gange findes genstande med de samme dimensioner, og alligevel er nogle lettere og andre er tungere, dette skyldes forskelle i tæthed. Den letteste genstand har en lavere tæthed end den tungeste.
Densitet er en intensiv egenskab af stof, som ikke afhænger af mængden af prøven, der undersøges, da det er forholdet mellem masse og volumen, der forbliver konstant for det samme stof. Dette gør det muligt at skelne et stof fra et andet.
Materialer har en bred vifte af tætheder, de laveste er dem af gasser, så enheden kg / m3 den er meget stor, og gram / liter eller g / l foretrækkes. Andre ofte anvendte enheder er gram / milliliter eller gram / kubikcentimeter.
Begrebet tæthed er især nyttigt, når man arbejder med kontinuerlige medier såsom væsker, hvad enten de er gasser eller væsker..
Densitetsformel
Ifølge den givne definition har densiteten en matematisk formel givet af:

Hvor densiteten er ρ, er m masse og V er volumen.
Hvordan måler du densiteten?
Tætheden af et objekt kan beregnes, hvis dets masse og volumen tidligere er målt. Sidstnævnte er ikke altid let, da prøven kan være uregelmæssig, men der er flere metoder.
Geometrisk metode
Hvis prøven har en regelmæssig geometrisk form, er der formler, der gør det muligt at beregne lydstyrken ud fra dens dimensioner. Med hensyn til massen kan dette opnås ved hjælp af en balance.
Testrørsmetode: volumenforskydning

Hvis genstanden ikke er regelmæssig, kan dens volumen bestemmes ved at måle det forskudte volumen ved at nedsænke det fuldstændigt i en væske såsom vand..
Til dette anvendes en gradueret beholder, og den fyldes med et nøjagtigt volumen vand V1, så er objektet helt neddykket, og det nye volumen V målesto. Objektets volumen er lig med forskellen V.to - V1.
For at anvende denne metode må prøvestoffet ikke opløses i vandet, og en målebeholder med passende størrelse skal være tilgængelig..
Tæthed ved hjælp af Archimedes 'princip
Archimedes 'princip kan bruges til at finde tætheden af en fast prøve. Princippet siger, at et legeme, der er helt eller delvist nedsænket i en væske, oplever en opadgående kraft kaldet stød, hvis størrelse er lig med vægten af den fortrængte væske, når kroppen placeres.
For at bestemme tætheden af et objekt ved hjælp af Archimedes 'princip følges følgende trin:
-
Trin 1
Bestem massen mc af objektet ved hjælp af en skala.
-
Trin 2
Fyld en beholder med en væske, hvis densitet er kendt, som normalt er destilleret vand. Denne værdi kaldes m1.
-
Trin 3
Nedsænk det faste objekt i beholderen helt med vand, og pas på, at det ikke berører væggene. Det observeres, at væsken udøver et tryk OG på det faste stof opad, og dette udøver igen ved Newtons tredje lov en reaktion af samme størrelse på vandet, men i den modsatte retning.
Ved at veje sættet, opnås den opnåede værdi, kaldet mto, vil være beholderen fyldt med vand plus denne reaktion.
-
Trin 4
Fra ligningen for densitet kan vi udtrykke kroppens volumen V, som er lig med volumenet af fortrængt væske:

Massen af den løsnede væske mF Det er simpelthen:
mF = mto −m1
Derfor:

Tæthedstyper
Absolut tæthed
Det er densiteten som defineret ovenfor: forholdet mellem masse og volumen af prøven.

Relativ tæthed
Ring også specifik tyngdekraft, Det er densiteten af et stof i forhold til et andet, der tages som reference. For faste stoffer og væsker er dette referencestof vand ved 4 ° C og 1 atm tryk, og for gasser er det tør luft. Det beregnes af:
Relativ densitet = massefylde af materiale / vandtæthed
Både materialets tæthed og vandets måling måles under de samme betingelser for tryk og temperatur og udtrykkes i de samme enheder..
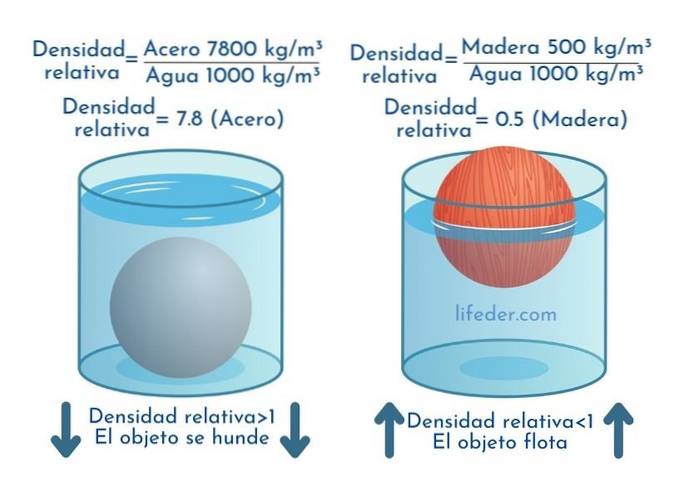
Det følgende billede viser de relative tætheder af stål og træ.

Da ståltætheden er 7800 kg / m3 og vandet er 1000 kg / m3, Den relative densitet af stål, betegnet som sg, er:
sg = 7800/1000 = 7,8
For sin del er den relative tæthed af træ:
sg = 500/1000 = 0,5
Objekter, hvis relative tæthed er mindre end 1, flyder i vand, mens dem, hvis relative densitet er større end 1 vask.
Tilsyneladende tæthed
Det beregnes af kvotienten mellem massen af prøven og dens volumen inklusive porer og rum med luft:
Tilsyneladende tæthed = masse / volumen = (masse partikler + Masse luft ) / (Lydstyrke partikler+ Bind luft)
Eksempler på tæthed
- Det letteste metal af alle er lithium med en densitet på 530 kg / m3
- Tætheden af blod er 1060 kg / m3
- Osmium er det mest kendte metal, med en densitet på 22 570 kg / m3
- Kvarkplasmaet har en densitet på 1 × 1019 kg / m3
Løst øvelser
Øvelse 1
Beregn korkens tæthed, vel vidende at en terning fremstillet med dette materiale, der måler 1,5 cm på en side, har en masse på 1 g.
-
Opløsning
Volumenet af en terning er:
V = ℓ3 = (1,5 cm)3 = 3,375 cm3
Erklæringen indikerer, at terningens masse m er m = 1 g, og derfor erstatter værdier i densitetsligningen:
ρ = m / V = 1 g / 3,375 cm3 = 0,296 g / cm3
Øvelse 2
Hvad er massen af en kugle lavet af osmium med en radius på 15 cm?
-
Opløsning
Startende fra densitetsligningen:

Massen ryddes som:
m = ρ ∙ V
Det er nødvendigt at beregne kuglens volumen, som er givet ved formlen:
Hvor r er kuglens radius. Da densiteten af osmium er 22570 kg / m3, Det er praktisk at udtrykke 15 cm i meter:
r = 15 cm = 15 × 10−2 m
V = (4/3) π × (15 × 10−2 m)3 = 0,01414 m3
Denne værdi erstattes i clearance for massen:
m = ρ ∙ V = 22570 kg / m3 × 0,01414 m3 = 319,1 kg
Referencer
- Chang, R. 2013. Kemi. 11. Udgave. McGraw Hill Uddannelse.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Shipman, J. 2009. En introduktion til fysik. Tolvte udgave. Brooks / Cole, Cengage Editions.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. Mcgraw bakke.
- University of Antioquia. Tæthed af faste stoffer. Gendannet fra: docencia.udea.edu.co.



Endnu ingen kommentarer