
Efterfølgende derivater (med løste øvelser)
Det successive derivater er derivaterne af en funktion efter det andet derivat. Processen til at beregne de successive derivater er som følger: vi har en funktion f, som vi kan udlede og således opnå den afledte funktion f '. Vi kan udlede dette afledte af f igen og opnå (f ')'.
Denne nye funktion kaldes det andet afledte; alle derivater beregnet fra det andet er successive; Disse, også kaldet højere orden, har store applikationer, såsom at give information om grafen for en funktion, testen af det andet derivat for relative ekstremer og bestemmelse af uendelige serier.

Artikelindeks
- 1 Definition
- 1.1 Eksempel 1
- 1.2 Eksempel 2
- 2 Hastighed og acceleration
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 applikationer
- 3.1 Implicit afledning
- 3.2 Eksempel
- 3.3 Relative ekstremer
- 3.4 Eksempel
- 3.5 Taylor-serien
- 3.6 Eksempel
- 4 Referencer
Definition
Ved hjælp af Leibniz's notation har vi, at afledningen af en funktion "y" med hensyn til "x" er dy / dx. For at udtrykke det andet afledte af "y" ved hjælp af Leibniz's notation, skriver vi som følger:

Generelt kan vi udtrykke successive derivater som følger med Leibniz's notation, hvor n repræsenterer rækkefølgen af derivatet.

Andre anvendte notationer er følgende:
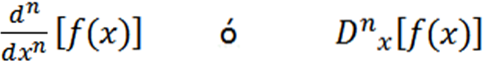
Nogle eksempler, hvor vi kan se de forskellige notationer, er:
Eksempel 1
Få alle derivater af funktionen f defineret af:
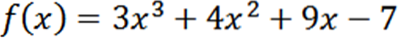
Ved hjælp af de sædvanlige afledningsteknikker har vi, at derivatet af f er:

Når vi gentager processen, kan vi opnå det andet derivat, det tredje derivat og så videre.
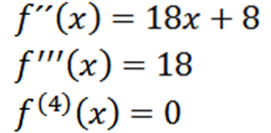
Bemærk, at det fjerde derivat er nul og derivatet af nul er nul, så vi har:

Eksempel 2
Beregn det fjerde afledte af følgende funktion:
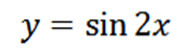
Ved at udlede den givne funktion har vi som et resultat:
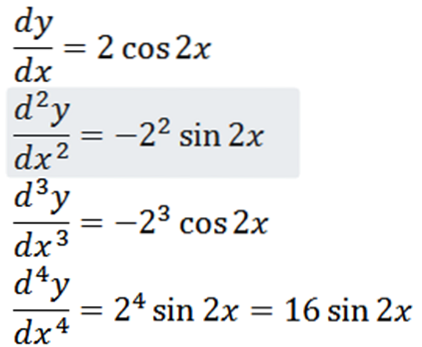
Hastighed og acceleration
En af motiverne, der førte til opdagelsen af derivatet, var søgningen efter definitionen af øjeblikkelig hastighed. Den formelle definition er som følger:
Lad y = f (t) være en funktion, hvis graf beskriver banen for en partikel på et øjeblik t, så er dens hastighed på et øjeblik t givet ved:

Når en partikels hastighed er opnået, kan vi beregne øjeblikkelig acceleration, som defineres som følger:
Den øjeblikkelige acceleration af en partikel, hvis vej er givet ved y = f (t), er:

Eksempel 1
En partikel bevæger sig langs en linje i henhold til positionsfunktionen:

Hvor "y" måles i meter og "t" i sekunder.
- På hvilket tidspunkt er dens hastighed 0?
- På hvilket tidspunkt er dens acceleration 0?
Når der udledes positionen "y", har vi, at dens hastighed og acceleration er givet henholdsvis ved:

For at besvare det første spørgsmål er det tilstrækkeligt at bestemme, hvornår funktionen v bliver nul; dette er:
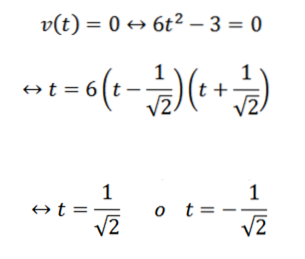
Vi fortsætter med følgende spørgsmål på en analog måde:

Eksempel 2
En partikel bevæger sig langs en linje i henhold til følgende bevægelsesligning:

Bestem "t, y" og "v" når a = 0.
At vide, at hastighed og acceleration er givet af

Vi fortsætter med at udlede og opnå:

At lave a = 0, vi har:
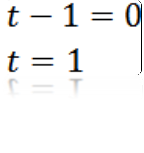
Fra hvor vi kan udlede, at værdien af t, så a er lig med nul, er t = 1.
Derefter vurderer vi positionsfunktionen og hastighedsfunktionen ved t = 1, har vi:

Ansøgninger
Eksplicit afledning
Efterfølgende derivater kan også opnås ved implicit afledning.
Eksempel
Givet følgende ellipse, find “y”:

Afledt implicit med hensyn til x har vi:
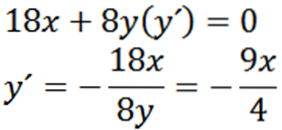
Derefter giver implicit genafledning med hensyn til x os:

Endelig har vi:
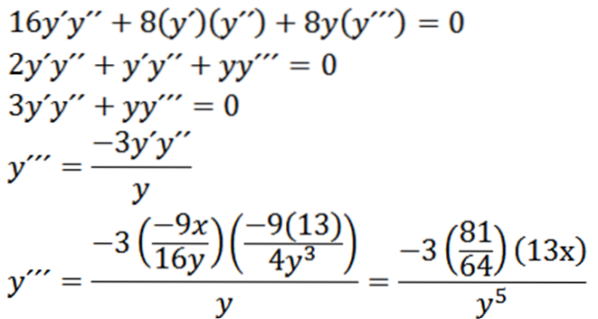
Relative ekstremer
En anden anvendelse, som vi kan give afledningerne af anden orden, er i beregningen af relative ekstremer af en funktion.
Kriteriet for det første afledte for lokale ekstremer fortæller os, at hvis vi har en kontinuerlig funktion f i et interval (a, b), og der findes et c, der hører til nævnte interval, så f 'forsvinder i c (det vil sige, at c er et kritisk punkt), kan en af tre tilfælde forekomme:
- Hvis f '(x)> 0 for enhver x, der tilhører (a, c) og f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
- Hvis f '(x) < 0 para cualquier x perteneciente a (a,c) y f'(x)>0 for x, der hører til (c, b), så er f (c) et lokalt minimum.
- Hvis f '(x) har det samme tegn i (a, c) og i (c, b), betyder det, at f (c) ikke er en lokal ekstrem.
Ved hjælp af kriteriet for det andet derivat kan vi vide, om et kritisk antal af en funktion er et lokalt maksimum eller et minimum uden at skulle se, hvad funktionstegnet er i de ovennævnte intervaller..
Det andet driftskriterium fortæller os, at hvis f '(c) = 0 og at f "(x) er kontinuerlig i (a, b), sker det, at hvis f" (c)> 0, så er f (c) en lokal minimum og hvis f "(c) < 0 entonces f(c) es un máximo local.
Hvis f "(c) = 0, kan vi ikke konkludere noget.
Eksempel
Givet funktionen f (x) = x4 + (4/3) x3 - 4xto, find de relative maksima og minima for f ved at anvende det andet derivatkriterium.
Først beregner vi f '(x) og f "(x), og vi har:
f '(x) = 4x3 + 4xto - 8x
f "(x) = 12xto + 8x - 8
Nu er f '(x) = 0 hvis, og kun hvis 4x (x + 2) (x - 1) = 0, og dette sker, når x = 0, x = 1 eller x = - 2.
For at bestemme, om de opnåede kritiske tal er relative ekstremer, er det nok at evaluere ved f "og således observere dets tegn.
f "(0) = - 8, så f (0) er et lokalt maksimum.
f "(1) = 12, så f (1) er et lokalt minimum.
f "(- 2) = 24, så f (- 2) er et lokalt minimum.
Taylor-serien
Lad f være en funktion defineret som følger:
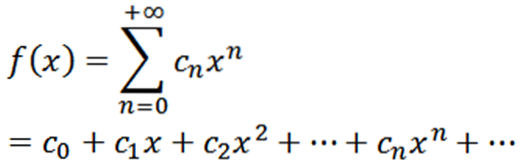
Denne funktion har en konvergensradius R> 0 og har derivater af alle ordrer i (-R, R). De successive derivater af f giver os:
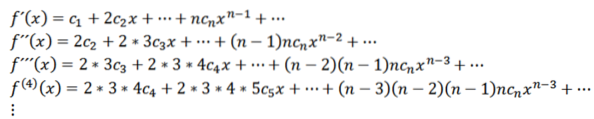
Hvis vi tager x = 0, kan vi opnå værdierne af cn baseret på dets derivater som følger:
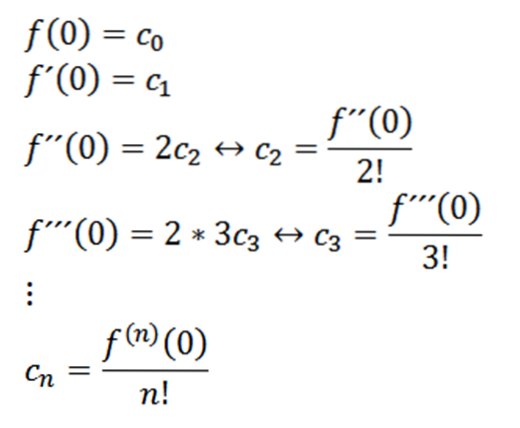
Hvis vi tager n = 0 som funktionen f (dvs. f ^ 0 = f), kan vi omskrive funktionen som følger:
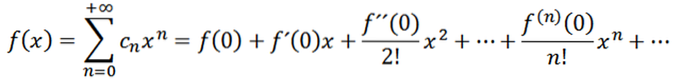
Lad os nu overveje funktionen som en række kræfter ved x = a:
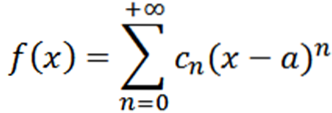
Hvis vi udfører en analyse, der er analog med den forrige, ville vi have, at vi kan skrive funktionen f som:
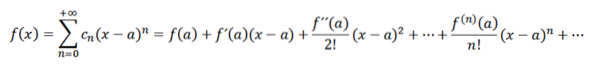
Disse serier er kendt som Taylor-serier fra f til a. Når a = 0 har vi den særlige sag, der kaldes Maclaurin-serien. Denne type serier er af stor matematisk betydning, især i numerisk analyse, da takket være disse kan vi definere funktioner i computere som ex , sin (x) og cos (x).
Eksempel
Hent Maclaurin-serien til ex.
Bemærk, at hvis f (x) = ex, derefter f(n)(x) = ex og f(n)(0) = 1, så din Maclaurin-serie er:
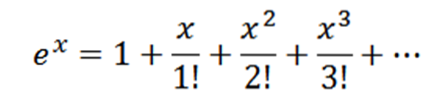
Referencer
- Frank Ayres, J. og Mendelson, E. (s.f.). Beregning 5ed. Mc Graw Hill.
- Leithold, L. (1992). Beregningen med analytisk geometri. HARLA, S.A.
- Purcell, E. J., Varberg, D. og Rigdon, S. E. (2007). Beregning. Mexico: Pearson Education.
- Saenz, J. (2005). Diferential beregning. Hypotenus.
- Saenz, J. (s.f.). Integreret beregning. Hypotenus.


Endnu ingen kommentarer