Det additiv nedbrydning af et positivt heltal er at udtrykke det som en sum af to eller flere positive heltal. Således har vi, at tallet 5 kan udtrykkes som 5 = 1 + 4, 5 = 2 + 3 eller 5 = 1 + 2 + 2. Hver af disse måder at skrive nummeret 5 er, hvad vi vil kalde additiv nedbrydning.
Hvis vi er opmærksomme, kan vi se, at udtrykkene 5 = 2 + 3 og 5 = 3 + 2 repræsenterer den samme sammensætning; de har begge de samme numre. Men for at gøre det nemmere skrives hvert af tilføjelserne normalt efter kriteriet fra laveste til højeste.
Artikelindeks
Som et andet eksempel kan vi tage tallet 27, som vi kan udtrykke som:
27 = 7 + 10 + 10
27 = 9 + 9 + 9
27 = 3 + 6 + 9 + 9
27 = 9 + 18
Additiv nedbrydning er et meget nyttigt værktøj, der giver os mulighed for at styrke vores viden om nummereringssystemer.
Når vi har tal med mere end to cifre, er en bestemt måde at nedbryde dem i multiplerne på 10, 100, 1000, 10 000 osv., Der udgør det. Denne måde at skrive ethvert nummer på kaldes kanonisk additiv nedbrydning. F.eks. Kan tallet 1456 nedbrydes som følger:
1456 = 1000 + 400+ 50 + 6
Hvis vi har nummeret 20 846 295, vil dets kanoniske additive nedbrydning være:
20 846 295 = 20.000.000 + 800.000 + 40.000 + 6000 + 200 + 90 +5.
Takket være denne nedbrydning kan vi se, at værdien af et givet ciffer er givet af den position, det indtager. Lad os tage tallene 24 og 42 som et eksempel:
24 = 20 + 4
42 = 40 +2
Her kan vi se, at i 24 har 2 en værdi på 20 enheder og 4 en værdi på 4 enheder; på den anden side, i 42 har 4 en værdi på 40 enheder og 2 på to enheder. Selvom begge tal bruger de samme cifre, er deres værdier således helt forskellige på grund af den position, de indtager.
En af de applikationer, som vi kan give til additiv nedbrydning, er i visse typer bevis, hvor det er meget nyttigt at se et positivt heltal som summen af andre.
Lad os tage et eksempel på følgende sætning med dens respektive beviser.
- Lad Z være et firecifret heltal, så kan Z deles med 5, hvis dens enhedsnummer er nul eller fem.
Lad os huske, hvad delbarhed er. Hvis vi har "a" og "b" heltal, siger vi at "a" deler "b" hvis der er et heltal "c" sådan at b = a * c.
En af egenskaberne ved delelighed fortæller os, at hvis "a" og "b" er delelige med "c", så er subtraktionen "a-b" også delelig..
Lad Z være et firecifret heltal; derfor kan vi skrive Z som Z = ABCD.
Ved hjælp af kanonisk additiv nedbrydning har vi:
Z = A * 1000 + B * 100 + C * 10 + D.
Det er klart, at A * 1000 + B * 100 + C * 10 kan deles med 5. Af denne grund har vi, at Z er deleligt med 5, hvis Z - (A * 1000 + B * 100 + C * 10) kan deles med 5.
Men Z - (A * 1000 + B * 100 + C * 10) = D og D er et enkelt cifret tal, så den eneste måde, hvorpå det kan deles med 5, er, at det er 0 eller 5.
Derfor kan Z deles med 5, hvis D = 0 eller D = 5.
Bemærk, at hvis Z har n cifre, er beviset nøjagtigt det samme, det ændrer kun, at vi nu ville skrive Z = A1TILto… TILn og målet ville være at bevise, at An det er nul eller fem.
Vi siger, at en opdeling af et positivt heltal er en måde, hvorpå vi kan skrive et tal som en sum af positive heltal.
Forskellen mellem en additiv nedbrydning og en partition er, at mens den første søger, at den i det mindste kan nedbrydes i to tilføjelser eller mere, har partitionen ikke denne begrænsning.
Således har vi følgende:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 2 + 2
Ovenstående er partitioner på 5.
Det vil sige, at vi har, at hver additiv nedbrydning er en partition, men ikke hver partition er nødvendigvis en additiv nedbrydning..
I talteori garanterer den grundlæggende sætning for aritmetik, at hvert heltal kan skrives entydigt som et produkt af primtal.
Når man studerer partitioner, er målet at bestemme på hvor mange måder et positivt heltal kan skrives som summen af andre heltal. Derfor definerer vi partitionsfunktionen som vist nedenfor.
Partitionsfunktionen p (n) er defineret som antallet af måder, hvorpå et positivt heltal n kan skrives som en sum af positive heltal.
Når vi vender tilbage til eksemplet på 5, har vi det:
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 1 + 1 + 1
Således er p (5) = 7.
Både partitioner og additive nedbrydninger af et tal n kan repræsenteres geometrisk. Antag, at vi har en additiv nedbrydning på n. I denne nedbrydning kan tilføjelserne arrangeres, så medlemmerne af summen ordnes fra mindst til størst. Så okay:
n = a1 + tilto + til3 +… + Ar med
til1 ≤ ato ≤ a3 ≤… ≤ ar.
Vi kan tegne denne nedbrydning på følgende måde: I en første række markerer vi a1-punkter, så markerer vi i det næsteto-point og så videre, indtil det når enr.
Tag for eksempel tallet 23 og dets følgende nedbrydning:
23 = 5 + 4 + 7 + 3 + 1 +3
Vi bestiller denne nedbrydning, og vi har:
23 = 1 + 3 + 3 + 4+ 5 + 7
Den tilsvarende graf ville være:
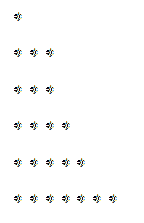
Ligeledes, hvis vi læser den nævnte graf lodret i stedet for vandret, kan vi opnå en nedbrydning, der muligvis er forskellig fra den foregående. I eksemplet med 23 skiller sig følgende ud:
Så vi har 23, vi kan også skrive det som:
23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.
Endnu ingen kommentarer