Det forskelle mellem hastighed og hastighed de eksisterer, selvom de begge er relaterede fysiske størrelser. På almindeligt sprog bruges det ene eller det andet udtryk om hinanden som om de var synonymer, men i fysik er det nødvendigt at skelne mellem dem..
Denne artikel definerer begge begreber, påpeger forskellene og forklarer ved hjælp af eksempler, hvordan og hvornår den ene eller den anden anvendes. For at forenkle betragter vi en partikel i bevægelse og derfra gennemgår vi begreberne hastighed og hastighed.
| Hastighed | Fart | |
| Definition | Det er den tilbagelagte afstand pr. Tidsenhed. | Det er forskydningen (eller ændring af position) i hver tidsenhed. |
| Notation | v | v |
| Matematisk objekttype | Klatre. | Vektor. |
| Formel (i en begrænset periode) * | v = Δs / Δt | v = Ar / At |
| Formel (i et givet øjeblik) ** | v = ds / dt = s '(t) | v = dr / dt = r '(t) |
| Forklaring af formlen | * Ruteens længde divideret med den tidsperiode, der bruges til at køre den. ** I øjeblikkelig hastighed har tidsperioden en tendens til nul. | * Vektorforskydning divideret med det tidsrum, hvor forskydningen opstod. |
| Egenskaber | For at udtrykke det kræves kun et positivt reelt tal, uanset de rumlige dimensioner, hvor bevægelsen opstår.. | Det kan tage mere end et reelt tal (positivt eller negativt) at udtrykke det afhængigt af de rumlige dimensioner, hvor bevægelsen opstår.. |
Forskellige aspekter af hastighed og hastighed blev opsummeret i tabellen ovenfor. Og så suppleres der med flere eksempler, der illustrerer de involverede begreber og deres forhold:
Antag, at en rød myre bevæger sig langs en lige linje og i den retning, der er angivet i nedenstående figur.
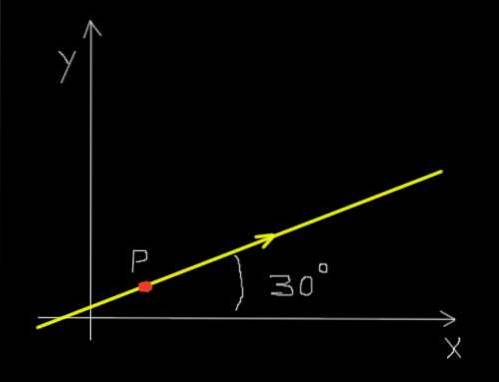
Derudover bevæger myren sig ensartet på en sådan måde, at den bevæger sig en afstand på 30 millimeter i en periode på 0,25 sekunder..
Bestem myrens hastighed og hastighed.
Myrens hastighed beregnes ved at dividere afstanden As rejste mellem tidsforløbet At.
v = Δs / Δt = (30 mm) / (0,25 s) = 120 mm / s = 12 cm / s
Myrens hastighed beregnes ved at dividere forskydningen Δr mellem det tidsrum, hvor forskydningen blev foretaget.
Forskydningen var 30 mm i retning 30 ° i forhold til X-aksen eller i kompakt form:
Δr = (30 mm ¦ 30º)
Det kan bemærkes, at forskydningen består af en størrelse og en retning, da det er en vektormængde. Alternativt kan forskydningen udtrykkes i henhold til dens kartesiske komponenter X og Y på denne måde:
Δr = (30 mm * cos (30º); 30 mm * sin (30º)) = (25,98 mm; 15,00 mm)
Myrens hastighed beregnes ved at dividere forskydningen med det tidsrum, hvor den blev foretaget:
v = Δr/ Δt = (25,98 mm / 0,25 sek; 15,00 mm / 0,25 sek) = (103,92; 60,00) mm / sek
Denne hastighed i kartesiske komponenter X og Y og i enheder på cm / s er:
v = (10.392; 6.000) cm / s.
Alternativt kan hastighedsvektoren udtrykkes i sin polære form (modul ¦ retning) som vist:
v = (12 cm / s ¦ 30º).
Bemærk: i dette eksempel, da hastigheden er konstant, falder gennemsnitshastigheden og den øjeblikkelige hastighed sammen. Modulet for den øjeblikkelige hastighed viser sig at være den øjeblikkelige hastighed.
Den samme myre i det foregående eksempel går fra A til B, derefter fra B til C og endelig fra C til A, efter den trekantede sti vist i den følgende figur.
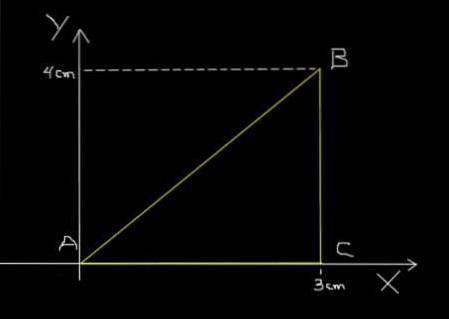
Afsnit AB dækker det i 0,2 sek. BC løber igennem det på 0,1 sek og til sidst løber CA igennem det på 0,3 sek. Beregn gennemsnitshastigheden for turen ABCA og den gennemsnitlige hastighed for turen ABCA.
For at beregne myrens gennemsnitshastighed begynder vi med at bestemme den samlede tilbagelagte afstand:
As = 5 cm + 4 cm + 3 cm = 12 cm.
Det anvendte tidsrum for hele rejsen er:
Δt = 0,2 s + 0,1 s + 0,3 s = 0,6 s.
Så myrens gennemsnitlige hastighed er:
v = Δs / Δt = (12 cm) / (0,6 s) = 20 cm / s.
Dernæst beregnes myrens gennemsnitshastighed i ABCA-ruten. I dette tilfælde er myrens forskydning:
Δr = (0 cm; 0 cm)
Dette skyldes, at forskydningen er forskellen mellem slutposition minus startposition. Da begge positioner er ens, er deres forskel nul, hvilket resulterer i en nul forskydning.
Denne nulforskydning blev udført i en periode på 0,6 sek, så myrens gennemsnitlige hastighed var:
v =(0 cm; 0 cm) / 0,6 s = (0; 0) cm / s.
Konklusion: gennemsnitshastighed 20 cm / s, men gennemsnitshastigheden er nul i ABCA-ruten.
Et insekt bevæger sig på en cirkel med en radius på 0,2 m med ensartet hastighed, således at det, startende fra A og ankommer til B, bevæger sig ¼ med en omkreds i 0,25 s.
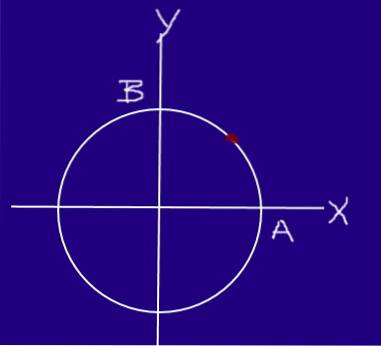
Bestem hastigheden og hastigheden af insektet i sektion AB.
Længden af omkredsbuen mellem A og B er:
Δs = 2πR / 4 = 2π (0,2 m) / 4 = 0,32 m.
Ved at anvende definitionen af gennemsnitshastighed har vi:
v = Δs / Δt = 0,32 m / 0,25 s = 1,28 m / s.
For at beregne gennemsnitshastigheden er det nødvendigt at beregne forskydningsvektoren mellem startposition A og slutposition B:
Δr = (0, R) - (R, 0) = (-R, R) = (-0,2, 0,2) m
Ved at anvende definitionen af gennemsnitshastighed får vi:
v = Δr/ Δt = (-0,2, 0,2) m / 0,25 s = (-0,8, 0,8) m / s.
Det forrige udtryk er gennemsnitshastigheden mellem A og B udtrykt i kartesisk form. Alternativt kan gennemsnitshastigheden udtrykkes i polær form, det vil sige modul og retning:
| v | = ((-0,8) ^ 2 + 0,8 ^ 2) ^ (½) = 1,13 m / s
Retning = arctan (0,8 / (-0,8)) = arctan (-1) = -45º + 180º = 135º i forhold til X-aksen.
Endelig er den gennemsnitlige hastighedsvektor i polær form: v =(1,13 m / s ¦ 135º).
Antages det, at insektets starttid i det foregående eksempel er 0s fra punkt A, har vi, at dets placeringsvektor på ethvert øjeblik t er givet ved:
r(t) = [R cos ((π / 2) t); R sin ((π / 2) t)].
Bestem hastighed og øjeblikkelig hastighed for ethvert øjeblik t.
Den øjeblikkelige hastighed er den afledte med hensyn til positionens funktionstid:
v(t) = dr/ dt = [-R (π / 2) sin ((π / 2) t); R (π / 2) cos ((π / 2) t)]
Den øjeblikkelige hastighed er modulet for den øjeblikkelige hastighedsvektor:
v (t) = | v(t) | = π R / 2 ^ ½
Endnu ingen kommentarer