Dynamik i et system med partikler eksempler, øvelser

Det dynamik i et partikelsystem Den består af anvendelsen af ​​Newtons bevægelseslove til et sæt partikler, som kan være diskrete (partiklerne kan tælles) eller udgøre en del af et udvidet objekt, i dette tilfælde er systemet kontinuerligt.

For at forklare bevægelsen af ​​et partikelsystem er det ubelejligt at analysere hver enkelt separat og se, hvilke kræfter der virker på det. I stedet defineres et repræsentativt punkt for sættet kaldet Massecenter.

At beskrive bevægelsen af ​​massecentret giver et meget nøjagtigt overblik over den samlede bevægelse af helheden, det tillader også anvendelse af Newtons love på en måde, der er analog med, når objektet betragtes som en dimensionsløs partikel.

Denne seneste model, kaldet partikelmodel, Det er godt til beskrivelse af oversættelser, og også når du ikke behøver at overveje objektets dimensioner. Men almindelige genstande har størrelse, og hvis de også har rotationsbevægelse, er det nødvendigt at tage højde for de punkter, hvorpå kræfterne påføres.

Artikelindeks

• 1 Eksempler
  • 1.1 Jorden og månen
  • 1.2 Udvidede objekter
• 2 Massepunktet for et partikelsystem
  • 2.1 CM bevægelse
  • 2.2 Kraft på CM
• 3 Øvelse løst
  • 3.1 Løsning a
  • 3.2 Løsning b
  • 3.3 Løsning c
• 4 Referencer

Eksempler

Jorden og månen

Et sæt diskrete partikler m₁, m_to, m₃... der til sidst bevæger sig med hensyn til oprindelsen af ​​et koordinatsystem på grund af en eller anden resulterende kraft, der virker på dem, er et godt eksempel på et partikelsystem.

Jorden kan betragtes som en partikel og månen som en anden, så udgør begge et system med 2 partikler under påvirkning af Solens tyngdekraft..

Udvidede objekter

En person, et dyr eller et hvilket som helst objekt i miljøet kan også betragtes som et system med partikler, kun at disse er så små, at de ikke kan tælles en efter en. Dette er et kontinuerligt system, men under hensyntagen til visse overvejelser er dets behandling den samme som for et diskret system.

Nedenfor er detaljerne.

Massepunktet for et partikelsystem

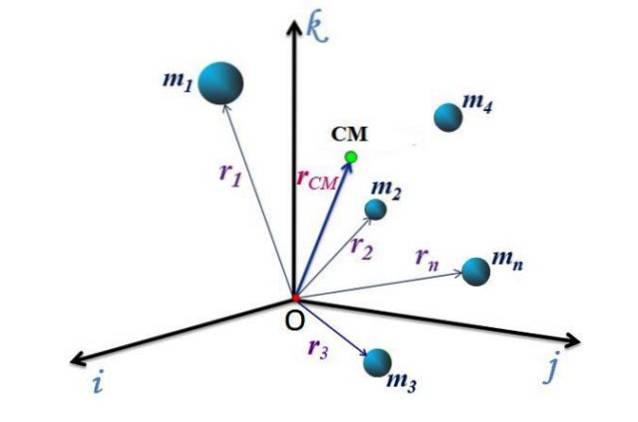
For at starte undersøgelsen af ​​et partikelsystem skal vi finde massecentret (CM), som er det punkt, hvor hele systemets masse er koncentreret..

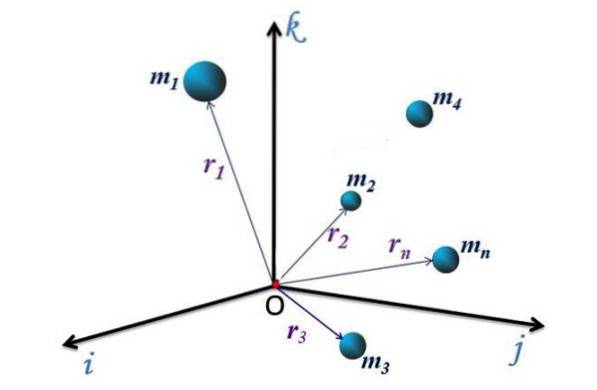
For det diskrete system i figur 1 med n partikler, har hver en positionsvektor rettet fra oprindelsen O for koordinatsystemet til det punkt P (x, y, z), hvor partiklen er. Disse vektorer betegnes som r₁, r_to, r₃... r_n.

Koordinaterne for CM beregnes ved hjælp af følgende ligninger:

Hvor hver af masserne i sættet er repræsenteret som m₁, m_to, m₃... m_n. Bemærk, at summeringen ∑ m_jeg svarer til den samlede masse M for samlingen. Hvis systemet er kontinuerligt, erstattes summeringen med integraler.

Hver af de vinkelrette retninger er repræsenteret af enhedsvektorerne jeg, j Y k, dermed betegnes positionsvektoren for CM r_CM, kan udtrykkes ved:

r_CM = x_CM jeg + Y_CM j + z_CM k

CM bevægelse

Når placeringen af ​​massecentret er kendt, gælder de kendte bevægelsesligninger. Hastigheden af ​​CM er det første afledte af positionen med hensyn til tid:

I dette tilfælde har systemet et samlet momentum P der beregnes som produktet af systemets samlede masse og hastigheden af ​​massecentret:

P = M ∙v_CM

Alternativt kan systemets samlede momentum beregnes direkte:

P = m₁v₁ + m_tov_to + m₃v₃ +…. = ∑ m_jeg v_jeg

Mens accelerationen af ​​CM er afledt af hastigheden:

Tving på CM

De kræfter, der virker på et partikelsystem, kan være:

• Interne kræfter på grund af interaktioner mellem de samme partikler.
• Eksterne kræfter, forårsaget af agenter uden for systemet.

Da de interne kræfter præsenteres parvis, af samme størrelse og retning, men modsatte retninger, ifølge Newtons tredje lov, er det rigtigt, at:

∑ F_int = 0

Derfor ændrer de interne kræfter ikke bevægelsen af ​​helheden, men de er meget vigtige for at bestemme den indre energi..

Hvis systemet er isoleret, og der ikke er nogen eksterne kræfter, er massecentrum ifølge Newtons første lov i ro eller bevæger sig med ensartet retlinet bevægelse. Ellers oplever massacentret en acceleration givet af:

∑ F_ekst = M ∙til_CM

Hvor M er systemets samlede masse. Ovenstående ligning kan skrives således:

Og det betyder, at den eksterne kraft svarer til den tidsmæssige variation i momentum, en anden måde at udtrykke Newtons anden lov på og den samme som den berømte engelske fysiker brugte i sin bog Princip.

Træning løst

Massepunktet for et 2-partikelsystem er på x-aksen i et bestemt øjeblik i position x = 2,0 m og bevæger sig med hastighed 5,0 m / s i samme retning og i positiv retning. Hvis den ene af partiklerne er ved oprindelsen, og den anden med en vægt på 0,1 kg, hviler ved x = 8,0 m, beregnes:

a) Massen af ​​partiklen, der er ved oprindelsen.

b) Systemets bevægelsesmængde

c) Hvad er partikelhastigheden ved oprindelsen?

Løsning til

Fra ligningen for placeringen af ​​massecentret:

r_CM = x_CM jeg + Y_CM j + z_CM k = 2,0 m jeg

Da CM kun har en x-koordinat, anvendes kun den første ligning af den tidligere angivne trio:

Nu er koordinaterne erstattet, hvis partiklen ved oprindelsen er betegnet som nummer 1 og den anden som nummer 2, er de numeriske data:

x₁ = 0 m, x_to = 8,0 m, m_to = 0,1 kg, x_CM = 2,0 m

Resterende:

Løsning b

Mængden af ​​systemets bevægelse beregnes af:

P = M ∙v_CM

Den samlede masse M er lig med:

M = 0,3 kg + 0,1 kg = 0,4 kg

Derfor:

P = 0,4 kg ∙ 5,0 m / s jeg = 2 kg.m / s jeg

Løsning c

Fra ligningen for P af et to-partikelsystem, rydder det v₁, da de andre data er kendte, da erklæringen siger, at partikel 2 er i ro, derfor:

v_to = 0 

Y P det ligner simpelthen:

P = m₁v₁

v₁ = P / m₁ = 2 kg.m / s jeg / 0,3 kg = 6,67 m / s jeg

Referencer

1. Duke University. Partikelsystemer. Gendannet fra: webhome.phy.duke.edu.
2. Rex, A. 2011. Grundlæggende fysik. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.
5. Tipler, P. (2006) Fysik til videnskab og teknologi. 5. udg. Bind 1. Editorial Reverté.