
Fordeling F karakteristika og øvelser løst
Det F fordeling o Fisher-Snedecor distribution er den, der bruges til at sammenligne afvigelser fra to forskellige eller uafhængige populationer, som hver følger en normalfordeling.
Fordelingen, der følger variansen af et sæt prøver fra en enkelt normalpopulation, er chi-kvadratfordelingen (Χto) af grad n-1, hvis hver af prøverne i sættet har n elementer.
For at sammenligne afvigelser fra to forskellige populationer er det nødvendigt at definere en statistisk, det vil sige en ekstra tilfældig variabel, der giver os mulighed for at skelne, om begge populationer har den samme varians eller ej.
Den nævnte hjælpevariabel kan direkte være kvotienten for prøvevarianterne for hver population, i hvilket tilfælde, hvis kvotienten er tæt på enhed, er der bevis for, at begge populationer har lignende afvigelser.
Artikelindeks
- 1 F-statistikken og dens teoretiske fordeling
- 1.1 Middel, tilstand og varians af F-fordelingen
- 2 Håndtering af F-distributionen
- 2.1 Tabeller over F-fordelingen
- 2.2 Software til F-distribution
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Referencer
F-statistikken og dens teoretiske fordeling
Den tilfældige variabel F eller F-statistik foreslået af Ronald Fisher (1890 - 1962) er den hyppigst anvendte til at sammenligne afvigelser fra to populationer og defineres som følger:
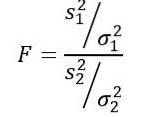
At være sto prøvevariansen og σto populationsvariansen. For at skelne mellem hver af de to befolkningsgrupper anvendes henholdsvis abonnement 1 og 2..
Det er kendt, at chi-kvadratfordelingen med (n-1) frihedsgrader er den, der følger den ekstra (eller statistiske) variabel, der er defineret nedenfor:
xto = (n-1) sto / σto.
Derfor følger F-statistikken en teoretisk fordeling givet ved følgende formel:
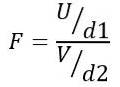
At være ELLER chi-kvadratfordelingen med d1 = n1 - 1 frihedsgrader for befolkning 1 og V chi-kvadratfordelingen med d2 = n2 - 1 frihedsgrader for befolkningen 2.
Kvotienten defineret på denne måde er en ny sandsynlighedsfordeling, kendt som F fordeling med d1 frihedsgrader i tælleren og d2 frihedsgrader i nævneren.
Gennemsnit, tilstand og varians af F-fordelingen
Halvt
Gennemsnittet af F-fordelingen beregnes som følger:
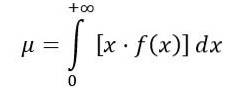
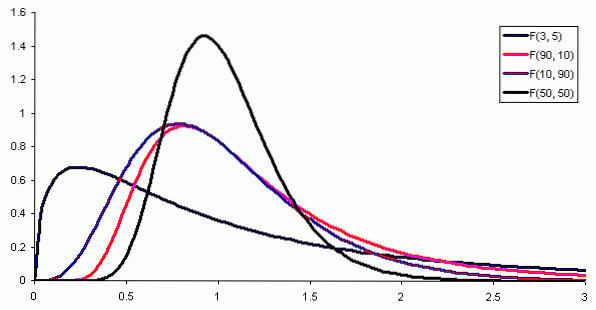
Hvor f (x) er sandsynligheden for F-fordelingen, som er vist i figur 1 for forskellige kombinationer af parametre eller frihedsgrader.
Vi kan skrive sandsynlighedstætheden f (x) som en funktion af funktionen Γ (gammafunktion):
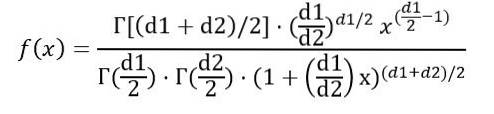
Når integralen angivet ovenfor er udført, konkluderes det, at gennemsnittet af F-fordelingen med frihedsgrader (d1, d2) er:
μ = d2 / (d2 - 2) med d2> 2
Hvor det bemærkes, at middelværdien nysgerrig ikke afhænger af tællerens frihedsgrader d1.
mode
På den anden side afhænger tilstanden af d1 og d2 og er givet af:
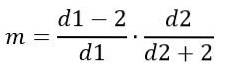
For d1> 2.
Variation af F-fordelingen
Variansen σto af F-fordelingen beregnes ud fra integralen:
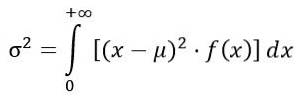
Opnåelse:
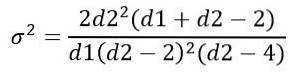
Håndtering af F-distributionen
Ligesom andre kontinuerlige sandsynlighedsfordelinger, der involverer komplicerede funktioner, sker håndteringen af F-distributionen ved hjælp af tabeller eller software..
Fordelingstabeller F
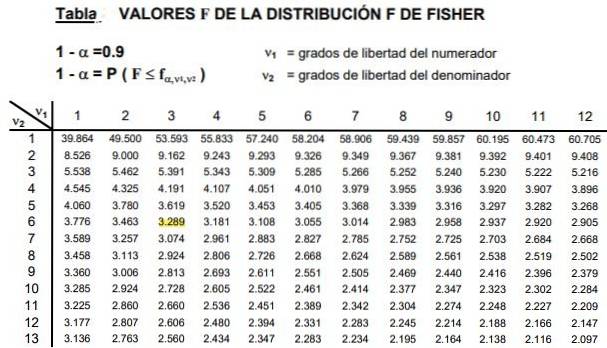
Tabellerne involverer de to parametre eller frihedsgrader for F-fordelingen, kolonnen angiver tællerens frihedsgrad og rækken nævners frihedsgrad.
Figur 2 viser et snit i tabellen over F-fordelingen i tilfælde af a signifikansniveau på 10%, dvs. a = 0,1. Værdien af F er fremhævet, når d1 = 3 og d2 = 6 med Selvtillidsniveau 1- α = 0,9 det vil sige 90%.
Software til F-distribution
Hvad angår softwaren, der håndterer F-distributionen, er der et stort udvalg, lige fra regneark som sådan Excel til specialiserede pakker som minitab, SPSS Y R for at nævne nogle af de bedst kendte.
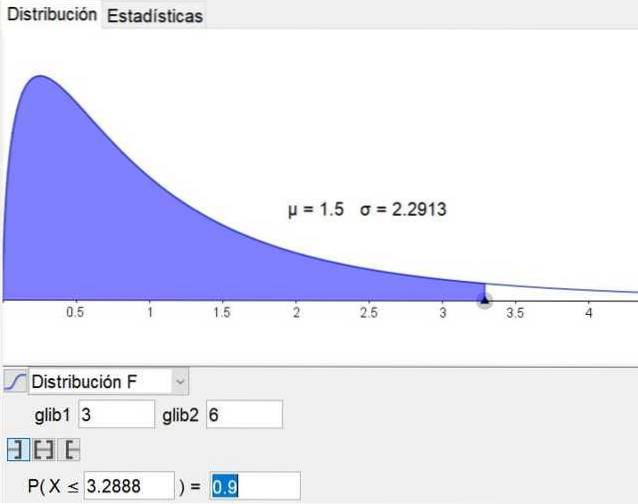
Det er bemærkelsesværdigt, at software til geometri og matematik geogebra har et statistisk værktøj, der inkluderer hovedfordelingerne inklusive F-fordelingen. Figur 3 viser F-fordelingen for sagen d1 = 3 og d2 = 6 med Selvtillidsniveau på 90%.
Løst øvelser
Øvelse 1
Overvej to prøver af populationer, der har den samme populationsvarians. Hvis prøve 1 har størrelse n1 = 5, og prøve 2 har størrelse n2 = 10, skal du bestemme den teoretiske sandsynlighed for, at kvotienten for deres respektive afvigelser er mindre end eller lig med 2.
Opløsning
Det skal huskes, at F-statistikken er defineret som:
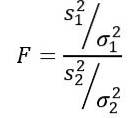
Men vi får at vide, at befolkningsafvigelserne er ens, så for denne øvelse gælder følgende:
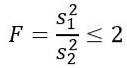
Da vi vil vide den teoretiske sandsynlighed for, at denne kvotient af prøvevariationer er mindre end eller lig med 2, er vi nødt til at kende området under F-fordelingen mellem 0 og 2, som kan opnås ved tabeller eller software. Til dette skal det tages i betragtning, at den krævede F-fordeling har d1 = n1 - 1 = 5 - 1 = 4 og d2 = n2 - 1 = 10 - 1 = 9, det vil sige F-fordelingen med frihedsgrader ( 4, 9).
Ved at bruge det statistiske værktøj til geogebra Det blev bestemt, at dette areal er 0,82, så det konkluderes, at sandsynligheden for, at kvotienten for prøvevariationer er mindre end eller lig med 2 er 82%.
Dyrke motion to
Der er to fremstillingsprocesser til tynde ark. Tykkelsen skal variere så lavt som muligt. Der tages 21 prøver fra hver proces. Prøven fra proces A har en standardafvigelse på 1,96 mikron, mens prøven fra proces B har en standardafvigelse på 2,13 mikron. Hvilke af processerne har mindst variation? Brug et afvisningsniveau på 5%.
Opløsning
Dataene er som følger: Sb = 2,13 med nb = 21; Sa = 1,96 med na = 21. Det betyder, at vi skal arbejde med en F-fordeling på (20, 20) frihedsgrader.
Nulhypotesen indebærer, at populationsvariansen for begge processer er identisk, det vil sige σa ^ 2 / σb ^ 2 = 1. Den alternative hypotese ville antyde forskellige populationsvariationer.
Under antagelse af identiske populationsvariationer defineres den beregnede F-statistik som: Fc = (Sb / Sa) ^ 2.
Da afstødningsniveauet er blevet taget som α = 0,05, er α / 2 = 0,025
Fordelingen F (0,025, 20,20) = 0,406, mens F (0,975, 20,20) = 2,46.
Derfor er nulhypotesen sand, hvis den beregnede F opfylder: 0,406≤Fc≤2,46. Ellers afvises nulhypotesen.
Da Fc = (2.13 / 1.96) ^ 2 = 1.18 konkluderes det, at Fc-statistikken ligger i acceptområdet for nulhypotesen med en sikkerhed på 95%. Med andre ord, med 95% sikkerhed, har begge fremstillingsprocesser den samme populationsvarians..
Referencer
- F Test for uafhængighed. Gendannet fra: saylordotorg.github.io.
- Med Wave. Statistikker anvendt på sundhedsvidenskab: F-testen. Hentet fra: medwave.cl.
- Sandsynligheder og statistikker. Distribution F. Gendannet fra: probayestadistica.com.
- Triola, M. 2012. Elementær statistik. 11. Udgave. Addison Wesley.
- UNAM. Distribution F. Gendannet fra: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Distribution F. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer