Det Normal fordeling eller Gaussisk fordeling er sandsynlighedsfordelingen i en kontinuerlig variabel, hvor sandsynlighedsdensitetsfunktionen er beskrevet af en eksponentiel funktion af kvadratisk og negativt argument, hvilket giver anledning til en klokkeform.
Navnet på normalfordeling kommer fra det faktum, at denne fordeling er den, der gælder for det største antal situationer, hvor en kontinuerlig tilfældig variabel er involveret i en given gruppe eller population..
Eksempler, hvor den normale fordeling anvendes, er: mænds eller kvinders højde, variationer i mål af en vis fysisk størrelse eller i målbare psykologiske eller sociologiske træk såsom den intellektuelle kvotient eller et bestemt produkts forbrugsvaner.
På den anden side kaldes det en Gaussisk fordeling eller Gaussisk klokke, fordi det er dette tyske matematiske geni, der krediteres sin opdagelse for den brug, han gav den til at beskrive den statistiske fejl i astronomiske målinger tilbage i år 1800..
Det anføres dog, at denne statistiske fordeling tidligere blev offentliggjort af en anden stor matematiker af fransk oprindelse, såsom Abraham de Moivre, tilbage i år 1733.
Artikelindeks
Til normalfordelingsfunktionen i den kontinuerlige variabel x, med parametre μ Y σ det er betegnet med:
N (x; μ, σ)
og det er eksplicit skrevet sådan:
N (x; μ, σ) = ∫-∞x f (s; μ, σ) ds
hvor f (u; μ, σ) er sandsynlighedsdensitetsfunktionen:
f (s; μ, σ) = (1 / (σ√ (2π)) Exp (- sto/ (2σto))
Den konstant, der multiplicerer den eksponentielle funktion i sandsynlighedsdensitetsfunktionen kaldes normaliseringskonstanten, og den er valgt på en sådan måde, at:
N (+ ∞, μ, σ) = 1
Det forrige udtryk sikrer, at sandsynligheden for, at den tilfældige variabel x er mellem -∞ og + ∞ er 1, det vil sige 100% sandsynlighed.
Parameter μ er det aritmetiske gennemsnit af den kontinuerlige tilfældige variabel x y σ standardafvigelsen eller kvadratroden af den samme variabels varians. I tilfælde af at μ = 0 Y σ = 1 så har vi den normale normalfordeling eller den normale normalfordeling:
N (x; μ = 0, σ = 1)
1- Hvis en tilfældig statistisk variabel følger en normal fordeling af sandsynlighedsdensitet f (s; μ, σ), de fleste data er grupperet omkring middelværdien μ og er spredt rundt på det på en sådan måde, at lidt over ⅔ af dataene er imellem μ - σ Y μ + σ.
2- Standardafvigelsen σ det er altid positivt.
3- Formen for densitetsfunktionen F ligner en klokke, hvorfor denne funktion ofte kaldes en Gaussisk klokke eller Gaussisk funktion.
4- I en Gaussisk fordeling falder middelværdien, medianen og tilstanden sammen.
5- Bøjningspunkterne for sandsynlighedsdensitetsfunktionen er placeret præcist ved μ - σ Y μ + σ.
6- Funktionen f er symmetrisk i forhold til en akse, der passerer gennem middelværdien μ y har asymptotisk nul for x ⟶ + ∞ og x ⟶ -∞.
7- Jo højere værdien af σ større spredning, støj eller afstand mellem dataene omkring middelværdien. Det vil sige til større σ klokkeformen er mere åben. I stedet σ lille indikerer, at terningerne er tæt på midten, og klokkens form er mere lukket eller spids.
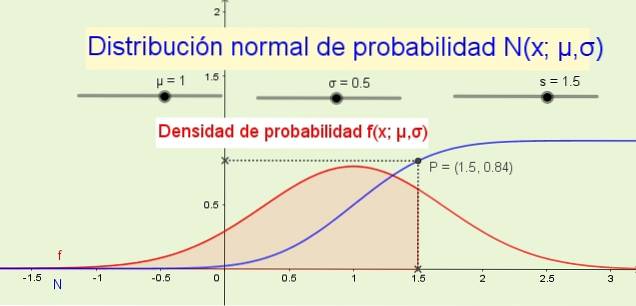
8- Fordelingsfunktionen N (x; μ, σ) angiver sandsynligheden for, at den tilfældige variabel er mindre end eller lig med x. For eksempel i figur 1 (ovenfor) sandsynligheden P, at variablen x er mindre end eller lig med 1,5 er 84% og svarer til arealet under sandsynlighedsdensitetsfunktionen f (x; μ, σ) fra -∞ til x.
9- Hvis dataene følger en normalfordeling, er 68,26% af disse mellem μ - σ Y μ + σ.
10- 95,44% af de data, der følger en normalfordeling, findes mellem μ - 2σ Y μ + 2σ.
11- 99,74% af de data, der følger en normalfordeling, er mellem μ - 3σ Y μ + 3σ.
12- Hvis en tilfældig variabel x følg en distribution N (x; μ, σ), derefter variablen
z = (x - μ) / σ følger standard normalfordeling N (z, 0,1).
Ændringen af variablen x til z Det kaldes standardisering eller typing, og det er meget nyttigt, når man anvender standarddistributionstabellerne på de data, der følger en ikke-standard normalfordeling..
For at anvende normalfordelingen er det nødvendigt at gennemgå beregningen af integriteten af sandsynlighedstætheden, hvilket fra det analytiske synspunkt ikke er let, og der er ikke altid et computerprogram, der tillader dets numeriske beregning. Til dette formål anvendes tabellerne over normaliserede eller standardiserede værdier, hvilket ikke er andet end normalfordelingen i sagen μ = 0 og σ = 1.
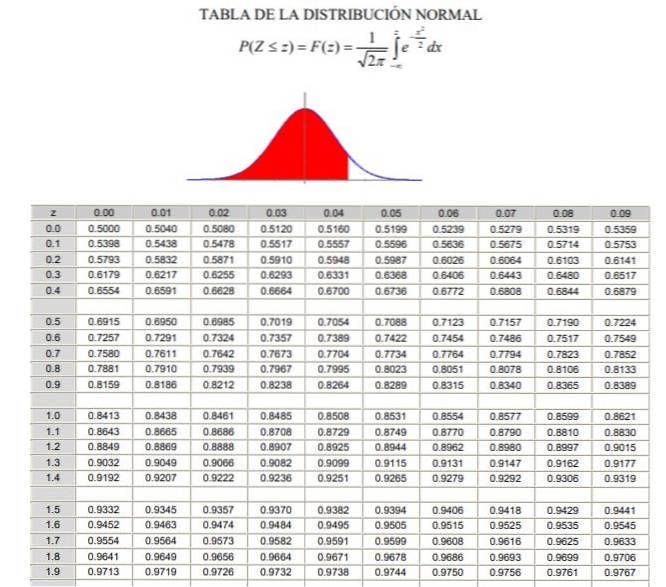
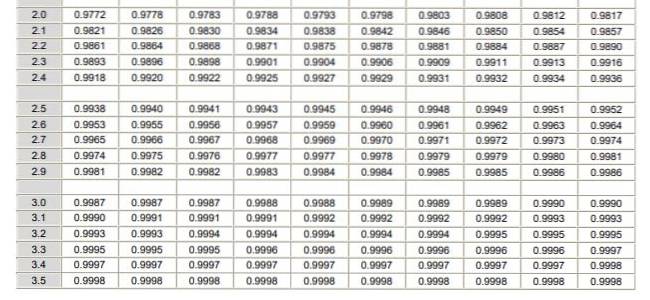
Det skal bemærkes, at disse tabeller ikke inkluderer negative værdier. Imidlertid kan de tilsvarende værdier opnås ved anvendelse af symmetriegenskaberne for den Gaussiske sandsynlighedsdensitetsfunktion. I nedenstående løste øvelse er brugen af tabellen i disse tilfælde angivet.
Antag, at du har et sæt tilfældige data x, der følger en normalfordeling af gennemsnit 10 og standardafvigelse 2. Du bliver bedt om at finde sandsynligheden for, at:
a) Den tilfældige variabel x er mindre end eller lig med 8.
b) Er mindre end eller lig med 10.
c) At variablen x er under 12.
d) Sandsynligheden for, at en værdi x er mellem 8 og 12.
Opløsning:
a) For at besvare det første spørgsmål skal du blot beregne:
N (x; μ, σ)
Med x = 8, μ = 10 Y σ = 2. Vi er klar over, at det er en integral, der ikke har en analytisk løsning i elementære funktioner, men løsningen udtrykkes som en funktion af fejlfunktionen erf (x).
På den anden side er der muligheden for at løse integralet i numerisk form, hvilket er, hvad mange regnemaskiner, regneark og computerprogrammer som GeoGebra gør. Følgende figur viser den numeriske løsning svarende til det første tilfælde:
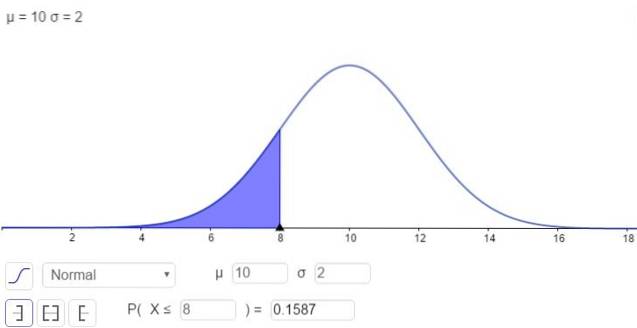
og svaret er, at sandsynligheden for, at x er under 8, er:
P (x ≤ 8) = N (x = 8; μ = 10, σ = 2) = 0,1587
b) I dette tilfælde forsøger vi at finde sandsynligheden for, at den tilfældige variabel x er under gennemsnittet, som i dette tilfælde er værd 10. Svaret kræver ingen beregning, da vi ved, at halvdelen af dataene er under gennemsnittet, og den anden halvdel over gennemsnittet. Derfor er svaret:
P (x ≤ 10) = N (x = 10; μ = 10, σ = 2) = 0,5
c) For at besvare dette spørgsmål skal du beregne N (x = 12; μ = 10, σ = 2), Dette kan gøres med en lommeregner, der har statistiske funktioner eller gennem software som GeoGebra:
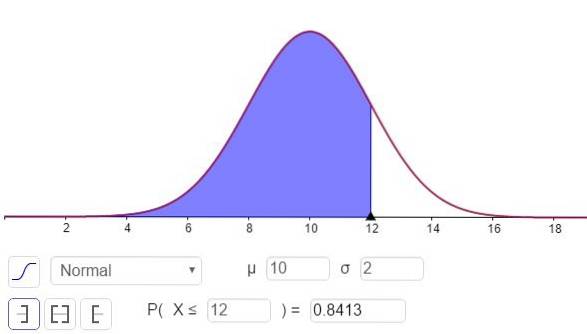
Svaret på del c kan ses i figur 3 og er:
P (x ≤ 12) = N (x = 12; μ = 10, σ = 2) = 0,8413.
d) For at finde sandsynligheden for, at den tilfældige variabel x er mellem 8 og 12, kan vi bruge resultaterne af del a og c som følger:
P (8 ≤ x ≤ 12) = P (x ≤ 12) - P (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26%.
Den gennemsnitlige pris på en virksomheds aktie er $ 25 med en standardafvigelse på $ 4. Bestem sandsynligheden for, at:
a) En handling koster mindre end $ 20.
b) Det koster mere end $ 30.
c) Prisen er mellem $ 20 og $ 30.
Brug standard normalfordelingstabeller til at finde svar.
Opløsning:
For at gøre brug af tabellerne er det nødvendigt at overføre til den normaliserede eller typede z-variabel:
$ 20 i den normaliserede variabel er lig z = ($ 20 - $ 25) / $ 4 = -5/4 = -1,25 og
$ 30 i den normaliserede variabel er lig z = ($ 30 - $ 25) / $ 4 = +5/4 = +1,25.
a) $ 20 er lig med -1,25 i den normaliserede variabel, men tabellen har ikke negative værdier, så vi placerer værdien +1,25, som giver værdien 0,8944.
Hvis 0,5 trækkes fra denne værdi, bliver resultatet det område mellem 0 og 1,25, som forresten er identisk (ved symmetri) med området mellem -1,25 og 0. Resultatet af subtraktionen er 0,8944 - 0,5 = 0,3944 hvilket er området mellem -1,25 og 0.
Men området fra -∞ til -1,25 er af interesse, som vil være 0,5 - 0,3944 = 0,1056. Det konkluderes derfor, at sandsynligheden for, at en aktie er under $ 20, er 10,56%.
b) $ 30 i den typede variabel z er 1,25. For denne værdi vises tallet 0,8944 i tabellen, hvilket svarer til området fra -∞ til +1,25. Området mellem +1,25 og + ∞ er (1 - 0,8944) = 0,1056. Det vil sige, at sandsynligheden for, at en aktie koster mere end $ 30, er 10,56%.
c) Sandsynligheden for, at en handling koster mellem $ 20 og $ 30, beregnes som følger:
100% -10,56% - 10,56% = 78,88%
Endnu ingen kommentarer