
Kontinuerlige ensartede fordelingsegenskaber, eksempler, applikationer
En tilfældig variabel har en kontinuerlig ensartet fordeling hvis sandsynligheden for, at den får en værdi inden for et endeligt interval [a, b], er den samme for ethvert underinterval af samme længde.
Denne fordeling er analog med den diskrete ensartede fordeling, som tildelte den samme sandsynlighed for hvert resultat af det tilfældige eksperiment, men i dette tilfælde er den variabel, der skal overvejes, kontinuerlig. Eksempelvis følger eksperimentet, der består i at vælge et reelt tal tilfældigt mellem værdierne a og b, den ensartede fordeling. Her er dens graf:
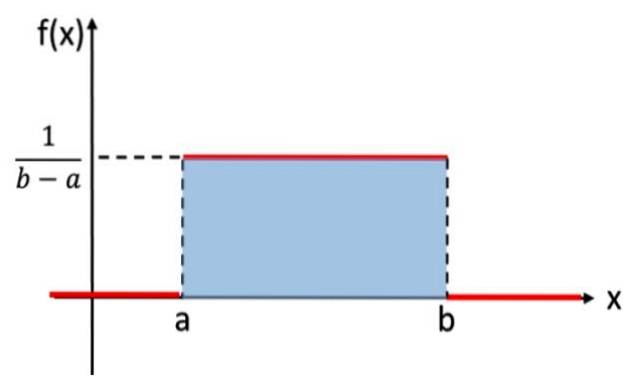
I matematisk notation har den kontinuerlige ensartede fordeling en densitetsfunktion defineret som en stykkevis eller stykkevis funktion, som kan skrives som:
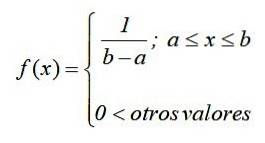
Grafen for denne funktion, kendt som tæthedskurve eller funktion, er et rektangel, derfor er den kontinuerlige ensartede fordeling også kendt som rektangulært layout y er den enkleste af de kontinuerlige fordelinger.
Arealet under grafen for en sandsynlighedsfordeling er lig med 1 og tager altid positive værdier. Den ensartede fordeling opfylder disse kriterier. Det er ikke nødvendigt at integrere direkte for at kontrollere, at området er 1, da området for det skraverede rektangel i figur 1 kan beregnes ved hjælp af formlen:
Areal = bund x højde = (b - a) x [1 / (b - a)] = 1
At kende området under densitetskurven er meget vigtigt, fordi der er et forhold mellem området og sandsynligheden for forekomst af en begivenhed, som for denne fordeling bestemmes i det næste afsnit.
Karakteristik af kontinuerlig ensartet distribution
Den kontinuerlige ensartede fordeling er kendetegnet ved dens:
Tæthedsfunktion
Lad X være den kontinuerlige tilfældige variabel, der hører til intervallet [a, b], og derefter:

Distributionsfunktion
Fordelingsfunktionen beregner sandsynligheden for, at den tilfældige variabel X tager en værdi x blandt de mulige værdier for intervallet [a, b]. For en kontinuerlig fordeling beregnes det generelt således:

I tilfælde af den kontinuerlige ensartede fordeling er sandsynligheden F (x) lig med arealet af rektanglet, hvis base er (x-a), og dets højde er (b-a):

Matematisk, hvis F (x) = Pr (X = x) oprettes følgende funktion i dele i henhold til det foregående resultat:

På denne måde bekræftes det, der blev sagt før: sandsynligheden afhænger kun af værdien af (x-a) og ikke af dens placering i intervallet [a, b]. Grafen for fordelingsfunktionen er:
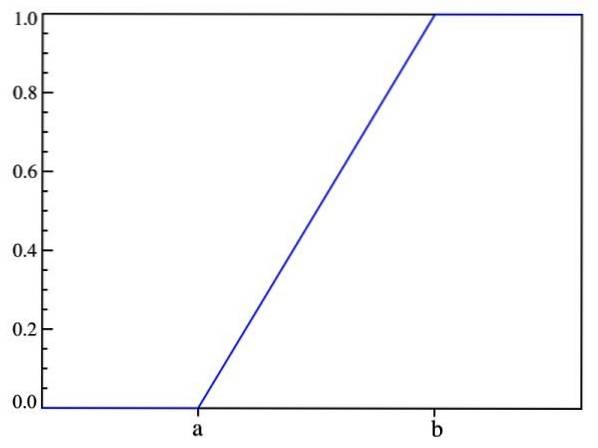
Forventet værdi, varians og standardafvigelse
Efter at have udført adskillige eksperimenter med den kontinuerlige tilfældige variabel kaldes dens gennemsnitlige værdi forventet værdi, betegnes som E (X) og beregnes ved hjælp af følgende integral:

V (X) = E (Xto) - E (X)to
Derfor:


D (X) = √ V (X)

Median, tilstand, symmetri og kurtose
Det kan let verificeres, at medianen, som er den centrale værdi af den ensartede fordeling, er lig med gennemsnittet, og da der ikke er nogen værdi, der gentager mere end andre, da alle er lige sandsynlige i intervallet [a, b] , mode eksisterer ikke.
Med hensyn til symmetri er den ensartede fordeling symmetrisk, og kurtosen, som er den grad, i hvilken værdierne er koncentreret omkring centrum, er -6/5.
Eksempler
Forskellige situationer kan modelleres gennem kontinuerlig distribution, og dermed kan deres adfærd forudsiges. Her er nogle eksempler:
Eksempel 1
Et firma, der leverer elektrisk service, leverer niveauer af spændinger, der er jævnt fordelt, mellem 123,0 V og 125,0 V. Dette betyder, at det i husstikkontakten er muligt at få en spændingsværdi, der hører til dette område..
Så som vist ovenfor er grafen for densitetsfunktionen rektanglet i rødt:

At beregne sandsynligheden for at have en spænding inden for det givne interval er meget let, for eksempel, hvad er sandsynligheden for, at virksomheden sender en spænding, der er lavere end 123,5 V?
Denne sandsynlighed er lig med arealet af rektanglet skygget i blåt:
P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25
Og hvad er sandsynligheden for, at den leverede spænding er større end 124,0 V.?
Da det samlede areal er lig med 1, er den søgte sandsynlighed:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Det giver mening, da 124.0 er nøjagtigt værdien i midten af intervallet.
Eksempel 2
En bestemt tilfældig variabel X har en ensartet fordeling i intervallet [0,100]. Beslutte:
a) Sandsynligheden for, at værdien af X er mindre end 22.
b) Sandsynligheden for, at X tager værdier mellem 20 og 35.
c) Den forventede værdi, varians og standardafvigelse for denne fordeling.
Svar til
Det bestemmes på samme måde som det foregående eksempel, men først skal vi bestemme højden af rektanglet og huske, at det samlede areal skal være lig med 1:
Areal = 100 × højde = 1
Derfor har rektanglet en højde lig med 1/100 = 0,01
P (X<22) = 22×0.01 = 0.22
Svar b
Den ønskede sandsynlighed er lig med arealet af rektanglet, hvis bredde er (35 - 20), og hvis højde er 0,01:
P (22 Hvis du foretrækker at gå direkte til fordelingsfunktionen ovenfor, er du bare nødt til at erstatte værdierne i: P (20≤X≤35) = F (35) -F (20) Med F (x) givet af: F (x) = (x-a) / (b-a) Værdierne, der skal indtastes, er: a = 0 b = 100 F (35) = (35-0) / (100-0) = 0,35 F (20) = (20-0) / (100-0) = 0,20 P (20≤X≤35) = 0,35-0,20 = 0,15 Den forventede værdi er: E (X) = (a + b) / 2 = (100 + 0) / 2 = 50 Variansen er: V (X) = (b-a)to/ 12 = (100-0)to/ 12 = 833,33 Og standardafvigelsen er: D (X) = √833,33 = 28,87 Denne fordeling er nyttig, når du udfører statistiske simuleringsprocesser, eller når du arbejder på begivenheder, hvis hyppighed af forekomst er regelmæssig.. Nogle programmeringssprog genererer tilfældige tal mellem 0 og 1, og som det kan ses af de foregående eksempler, er den fulgte sandsynlighedsfordeling ensartet. I dette tilfælde er intervallet, der skal overvejes, [0,1]. Hvis du har et eksperiment, hvor begivenhederne har regelmæssighed, som forklaret før, kan du i princippet tildele hver enkelt den samme sandsynlighed for forekomst. I dette tilfælde giver den sandsynlige model for ensartet distribution information til analysen.. Den ensartede fordeling bruges også til at afrunde forskellene mellem de observerede værdier og de reelle værdier for en variabel, forudsat at en ensartet fordeling af fejlen i et givet interval, ifølge afrunding, normalt fra -0,5 til +0,5.Svar c
Ansøgninger
Tilfældig talgenerering
Prøveudtagning af vilkårlige fordelinger
Afrunding af fejl
Referencer



Endnu ingen kommentarer