
Basisvektorrum og dimension, aksiomer, egenskaber
EN vektorial plads er et ikke-tomt sæt V= eller, v, w,..., hvis elementer er vektorer. Nogle vigtige operationer udføres med dem, blandt hvilke følgende skiller sig ud:
- Summen mellem to vektorer u + v hvilke resultater z, der hører til sættet V.
- Multiplikation af et reelt tal α med en vektor v: a v hvad giver en anden vektor Y som hører til V.

For at betegne en vektor bruger vi fed (v er en vektor), og for skalarer eller tal er græske bogstaver (α et tal).
Artikelindeks
- 1 Aksiomer og egenskaber
- 2 Eksempler på vektorrum
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 2.4 Eksempel 4
- 3 Basis og dimension af et vektorrum
- 3.1 Base
- 3.2 Dimension
- 3.3 Vector underrum
- 4 Løst øvelser
- 4.1-Øvelse 1
- 4.2-Øvelse 2
- 4.3-Øvelse 3
- 5 Referencer
Aksiomer og egenskaber
For at der skal gives et vektorrum skal følgende otte aksiomer være opfyldt:
1-omskiftelig: eller +v = v +eller
2-Transitivitet: (eller + v) + w = eller + ( v + w)
3-Eksistensen af nulvektoren 0 sådan at 0 + v = v
4-Eksistensen af det modsatte: det modsatte af v det er (-v) , som v + (-v) = 0
5-Distributivitet af produktet med hensyn til vektorsummen: α ( eller + v ) = αeller +av
6-Distributivitet af produktet med hensyn til den skalære sum: (α + β)v = αv +βv
7-associativitet af det skalære produkt: α (β v) = (α β)v
8-nummeret 1 er det neutrale element siden: 1v = v
Eksempler på vektorrum
Eksempel 1
Vektorer i (R²) -planet er et eksempel på et vektorrum. En vektor i planet er et geometrisk objekt, der har både størrelse og retning. Det er repræsenteret af et orienteret segment, der hører til nævnte plan og med en størrelse, der er proportional med dets størrelse.
Summen af to vektorer i planet kan defineres som den geometriske translationsoperation af den anden vektor efter den første. Resultatet af summen er det orienterede segment, der starter fra oprindelsen af det første og når spidsen af det andet.
På figuren kan det ses, at summen i R² er kommutativ.
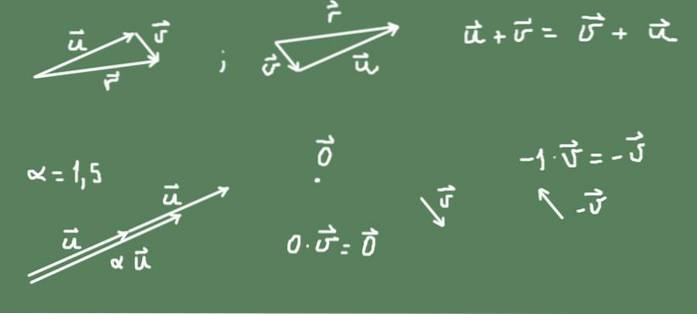
Produktet af et tal α og en vektor er også defineret. Hvis tallet er positivt, bevares retningen af den oprindelige vektor, og størrelsen er α gange den oprindelige vektor. Hvis tallet er negativt, er retningen modsat, og størrelsen af den resulterende vektor er den absolutte værdi af tallet.
Vektoren modsat enhver vektor v det er -v = (- 1) v.
Nullvektoren er et punkt i R2-planet, og antallet nul gange en vektor resulterer i nulvektoren.
Alt sagt er illustreret i figur 2.
Eksempel 2
Sæt P af alle polynomer med grad mindre end eller lig med to, inklusive grad nul, danner et sæt, der tilfredsstiller alle aksiomerne i et vektorrum.
Lad polynomet P (x) = a x² + b x + c og Q (x) = d x² + e x + f
Summen af to polynomer er defineret: P (x) + Q (x) = (a + d) x² + (b + e) x + (c + f)
Summen af polynomer, der hører til sættet P er kommutativ og transitiv.
Nullpolynomet tilhørende sættet P er den, der har alle dens koefficienter lig med nul:
0 (x) = 0 x² + 0 x + 0
Summen af en skalar α med et polynom defineres som: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c
Det modsatte polynom af P (x) er -P (x) = (-1) P (x).
Af alt det ovenstående følger det, at sættet P af alle polynomer med en grad, der er mindre end eller lig med to, er et vektorrum.
Eksempel 3
Sæt M af alle matricer i m rækker x n kolonner, hvis elementer er reelle tal, danner et reelt vektorrum med hensyn til operationerne for tilføjelse af matricer og produkt af et tal ved en matrix.
Eksempel 4
Sættet F for kontinuerlige funktioner af den reelle variabel danner et vektorrum, da det er muligt at definere summen af to funktioner, multiplikationen af en skalar med en funktion, nulfunktionen og den symmetriske funktion. De opfylder også aksiomerne, der karakteriserer et vektorrum.
Basis og dimension af et vektorrum
Grundlag
Grundlaget for et vektorrum er defineret som et sæt lineært uafhængige vektorer, således at der fra en lineær kombination af dem kan genereres en hvilken som helst vektor af dette vektorrum.
Lineær kombination af to eller flere vektorer består i at multiplicere vektorerne med en eller anden skalar og derefter tilføje dem vektorielt.
F.eks. Anvendes i vektorrummet af vektorer i tre dimensioner dannet af R3 det kanoniske grundlag defineret af enhedsvektorerne (af størrelsesorden 1) jeg, j, k.
Hvor jeg = (1, 0, 0); j = (0, 1, 0); k = (0, 0, 1). Disse er de kartesiske eller kanoniske vektorer.
Enhver vektor V tilhørende R³ er skrevet som V = a jeg + b j + c k, som er en lineær kombination af basisvektorerne jeg, j, k. Skalarer eller tal a, b, c er kendt som de kartesiske komponenter af V.
Det siges også, at basisvektorerne i et vektorrum danner et generatorsæt af vektorrummet.
Dimension
Dimensionen af et vektorrum er hovedtallet på et vektorgrundlag for dette rum; det vil sige antallet af vektorer, der udgør basen.
Denne kardinal er det maksimale antal lineært uafhængige vektorer i dette vektorrum og samtidig det mindste antal vektorer, der danner et generatorsæt af dette rum.
Baserne i et vektorrum er ikke unikke, men alle baserne i det samme vektorrum har den samme dimension.
Vector underrum
Et vektors underrum S for et vektorrum V er et delmængde af V, hvor de samme operationer er defineret som i V og opfylder alle vektorrumsaksiomer. Derfor vil underområdet S også være et vektorrum.
Et eksempel på et vektorunderrum er vektorerne, der hører til XY-planet. Dette underrum er en delmængde af et vektorrum med dimensionalitet større end det sæt vektorer, der hører til det tredimensionelle rum XYZ.
Et andet eksempel på et vektorunderrum S1 i vektorrummet S dannet af alle 2 × 2-matricer med reelle elementer er defineret nedenfor:
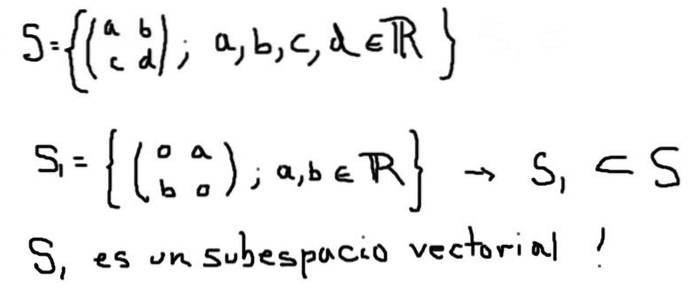
På den anden side udgør S2, der er defineret nedenfor, selvom det er en delmængde af S, ikke et vektorunderrum:

Løst øvelser
-Øvelse 1
Lad vektorerne være V1= (1, 1, 0); V2= (0, 2, 1) og V3= (0, 0, 3) i R³.
a) Vis, at de er lineært uafhængige.
b) Vis at de danner en base i R³, da enhver tredobbelt (x, y, z) kan skrives som en lineær kombination af V1, V2, V3.
c) Find komponenterne i triplen V = (-3,5,4) ved basen V1, V2, V3.
Opløsning
Kriteriet for at demonstrere lineær uafhængighed består i at etablere følgende sæt ligninger i α, β og γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
Hvis den eneste løsning på dette system er α = β = γ = 0, er vektorerne lineært uafhængige, ellers er de ikke.
For at opnå værdierne af α, β og γ foreslår vi følgende ligningssystem:
α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0
α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0
α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0
Den første fører til α = 0, den anden α = -2 ∙ β, men da α = 0 så er β = 0. Den tredje ligning indebærer, at γ = (- 1/3) β, men da β = 0 så er γ = 0.
Svar til
Det konkluderes, at det er et sæt lineært uafhængige vektorer i R³ .
Svar b
Lad os nu skrive tredobbelt (x, y, z) som en lineær kombination af V1, V2, V3.
(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α ∙ 1 + β ∙ 0 + γ ∙ 0 = x
α ∙ 1 + β ∙ 2 + γ ∙ 0 = y
α ∙ 0 + β ∙ 1 + γ ∙ 3 = z
Hvor har du:
α = x
α + 2 β = y
β + 3 y = z
Den første indikerer α = x, den anden β = (y-x) / 2 og den tredje γ = (z- y / 2 + x / 2) / 3. På denne måde har vi fundet generatorerne af α, β og γ for enhver triplet af R³
Svar c
Lad os gå videre for at finde komponenterne i triplen V = (-3,5,4) ved basen V1, V2, V3.
Vi erstatter generatorerne de tilsvarende værdier i de ovenfor nævnte udtryk.
I dette tilfælde har vi: α = -3; β = (5 - (- 3)) / 2 = 4; γ = (4- 5/2 + (- 3) / 2) / 3 = 0
Det er:
(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)
Sidst:
V = -3 V1 + 4 V2 + 0 V3
Det konkluderer vi V1, V2, V3 danne en basis i vektorrummet R³ i dimension 3.
-Øvelse 2
Udtryk polynomet P (t) = t² + 4t -3 som en lineær kombination af P1 (t) = t² -2t + 5, P2 (t) = 2t² -3t og P3 (t) = t + 3.
Opløsning
P (t) = x P1 (t) + y P2 (t) + z P3 (t)
hvor tallene x, y, z skal bestemmes.
Multiplikation og gruppering af termer med samme grad i t giver:
t² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)
Hvilket fører os til følgende ligningssystem:
x + 2y = 1
-2x -3y + z = 4
5x + 3z = -3
Løsningerne i dette ligningssystem er:
x = -3, y = 2, z = 4.
Det er:
P (t) = -3 P1 (t) + 2 P2 (t) + 4 P3 (t)
-Øvelse 3
Vis, at vektorerne v1= (1, 0, -1, 2); v2= (1, 1, 0, 1) og v3= (2, 1, -1, 1) af R1 er lineært uafhængige.
Opløsning
Vi kombinerer lineært de tre vektorer v1, v2, v3 og vi kræver, at kombinationen tilføjer null-elementet i R⁴
til v1 + b v2 + c v3 = 0
Nemlig,
a (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)
Dette fører os til følgende ligningssystem:
a + b + 2 c = 0
b + c = 0
-a - c = 0
2 a + b + c = 0
Ved at trække det første og det fjerde har vi: -a + c = 0, hvilket indebærer a = c.
Men hvis vi ser på den tredje ligning, har vi det a = -c. Den eneste måde, som a = c = (- c) holder, er at c er 0 og derfor vil a også være 0.
a = c = 0
Hvis vi erstatter dette resultat i den første ligning, konkluderer vi, at b = 0.
Endelig er a = b = c = 0, så det kan konkluderes, at vektorerne v1, v2 og v3 er lineært uafhængige.
Referencer
- Lipschutz, S. 1993. Lineær algebra. Anden version. McGraw-Hill. 167 - 198.



Endnu ingen kommentarer