
Inferentiel statistikhistorie, egenskaber, hvad den er beregnet til, eksempler

Det Inferential statistik eller deduktiv statistik er en, der udleder karakteristika for en population fra prøver taget fra den gennem en række analyseteknikker. Med den opnåede information udvikles modeller, der derefter giver mulighed for at forudsige om befolkningens opførsel..
Af denne grund er inferentiel statistik blevet den førende videnskab i at tilbyde den støtte og de instrumenter, som utallige discipliner kræver, når man træffer beslutninger..

Fysik, kemi, biologi, teknik og samfundsvidenskab drager løbende fordel af disse værktøjer, når de opretter deres modeller og designer og implementerer eksperimenter..
Artikelindeks
- 1 Kort historie med inferentiel statistik
- 1.1 Romerske imperium
- 1.2 Middelalderen
- 1.3 Moderne tidsalder
- 1.4 Samtidsalder
- 2 funktioner
- 3 Hvad er beskrivende statistik til? Ansøgninger
- 3.1 Sociologi og demografiske studier
- 3.2 Ingeniørarbejde
- 3.3 Økonomi og forretningsadministration
- 4 Eksempler på inferentiel statistik
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 5 grundlæggende begreber i inferentiel statistik
- 5.1 Begivenhed
- 5.2 Prøveplads
- 5.3 Befolkning og prøve
- 5.4 Prøveudtagning
- 5.5 Statistiske variabler
- 5.6 Sandsynlighedsfordelinger
- 5.7 Parametre og statistik
- 5.8 Statistisk hypotese
- 5.9 Hypotesetests
- 6 Emner af interesse
- 7 Referencer
Kort historie med inferentiel statistik
Statistik opstod i oldtiden på grund af behovet for mennesker til at organisere ting og optimere ressourcer. Før opfindelsen af skrivning blev der ført optegnelser over antallet af mennesker og den tilgængelige husdyr ved hjælp af symboler, der var indgraveret i sten..
Senere efterlod de kinesiske, babyloniske og egyptiske herskere data om mængden af afgrøder og antallet af indbyggere, indgraveret på lerplader, søjler og monumenter..
Romerriget
Da Rom udøvede sit herredømme i Middelhavet, var det almindeligt, at myndighederne foretog folketællinger hvert femte år. Faktisk kommer ordet "statistik" fra det italienske ord statista, hvad betyder det at udtrykke.
Samtidig holdt de store præ-colombianske imperier i Amerika også lignende optegnelser.
Middelalderen
I middelalderen registrerede Europas regeringer såvel som kirken ejerskab af jord. Derefter gjorde de det samme med fødsler, dåb, ægteskaber og dødsfald.
Moderne tidsalder
Den engelske statistiker John Graunt (1620-1674) var den første til at forudsige baseret på sådanne lister, såsom hvor mange mennesker der kunne dø af visse sygdomme og den anslåede andel af mandlige og kvindelige fødsler. Af denne grund betragtes han som far til demografi..
Samtidsalder
Senere, med fremkomsten af sandsynlighedsteorien, ophørte statistikken med at være en simpel samling af organisatoriske teknikker og opnåede et uventet omfang som en forudsigende videnskab..
Eksperterne kunne således begynde at udvikle modeller for befolkningers opførsel og med dem udlede, hvad der kunne ske med mennesker, objekter og endda ideer.
Egenskaber

Nedenfor har vi de mest relevante egenskaber ved denne gren af statistikker:
- Inferentiel statistik undersøger en befolkning, der tager en repræsentativ stikprøve derfra.
- Valget af prøven udføres ved forskellige procedurer, hvor de mest egnede er dem, der vælger komponenterne tilfældigt. Således har ethvert element i befolkningen den samme sandsynlighed for at blive valgt, og dermed undgås uønskede fordomme..
- At organisere de indsamlede oplysninger gør brug af beskrivende statistik.
- Statistiske variabler beregnes på prøven, der bruges til at estimere befolkningens egenskaber..
- Inferentiel eller deduktiv statistik bruger sandsynlighedsteori til at studere tilfældige begivenheder, det vil sige dem, der opstår tilfældigt. Hver begivenhed tildeles en vis sandsynlighed for forekomst.
- Den konstruerer hypoteser - antagelser - om befolkningens parametre og kontraster dem for at finde ud af, om de er korrekte eller ej, og beregner også konfidensniveauet for svaret, det vil sige, det giver en fejlmargin. Den første procedure kaldes hypotese testning, mens fejlmarginen er konfidensinterval.
Hvad er beskrivende statistik til? Ansøgninger

At studere en befolkning i sin helhed kan kræve en masse ressourcer i penge, tid og kræfter. Det foretrækkes at tage repræsentative prøver, der er meget mere håndterbare, indsamle data fra dem og skabe hypoteser eller antagelser om prøveadfærd.
Når hypoteserne er fastlagt, og deres gyldighed er testet, udvides resultaterne til befolkningen og bruges til at træffe beslutninger..
De hjælper også med at oprette modeller for denne befolkning, til at foretage fremskrivninger for fremtiden. Derfor er inferentiel statistik en meget nyttig videnskab til:
Sociologi og demografiske studier
Disse er ideelle anvendelsesområder, da statistiske teknikker anvendes med ideen om at etablere forskellige modeller for menneskelig adfærd. Noget, som a priori er ret kompliceret, da adskillige variabler griber ind.
I politik bruges det i vid udstrækning ved valgtid at kende vælgernes tendens til at stemme, på denne måde udformer partierne strategier.
ingeniørarbejde
Inferentielle statistikmetoder anvendes i vid udstrækning inden for ingeniørarbejde, hvor de vigtigste applikationer er kvalitetskontrol og procesoptimering, for eksempel forbedring af tidspunkterne for udførelse af opgaver samt forebyggelse af arbejdsulykker..
Økonomi og forretningsadministration
Med deduktive metoder kan du udføre fremskrivninger om en virksomheds drift, det forventede salgsniveau samt hjælp til beslutninger.
For eksempel kan deres teknikker bruges til at estimere, hvad købernes reaktion på et nyt produkt skal lanceres på markedet..
Det tjener også til at evaluere, hvordan ændringer i folks forbrugsvaner er givet vigtige begivenheder, såsom COVID-epidemien..
Eksempler på inferentiel statistik
Eksempel 1
Et simpelt deduktivt statistikproblem er følgende: En matematiklærer har ansvaret for 5 sektioner af elementær algebra på et universitet og beslutter at bruge de gennemsnitlige karakterer på bare en af dets sektioner for at estimere gennemsnittet af alle.

En anden mulighed er at tage en prøve fra hver sektion, studere dens karakteristika og udvide resultaterne til alle sektioner..
Eksempel 2
Lederen af en tøjbutik til kvinder vil vide, hvor meget en bestemt bluse vil sælge i sommersæsonen. For at gøre dette analyserer det salget af tøjet i løbet af de første to uger af sæsonen og bestemmer dermed tendensen..
Grundlæggende begreber i inferentiel statistik
Der er flere nøglebegreber, herunder dem, der kommer fra sandsynlighedsteori, som du skal være klar over for at forstå det fulde omfang af disse teknikker. Nogle, som en population og prøve, har vi allerede nævnt i hele teksten.
Begivenhed
En begivenhed eller begivenhed er noget der sker, og det kan have flere resultater. Et eksempel på en begivenhed kan være at vende en mønt, og der er to mulige resultater: hoveder eller haler.
Prøveplads
Det er sættet med alle mulige resultater af en begivenhed.
Befolkning og prøve
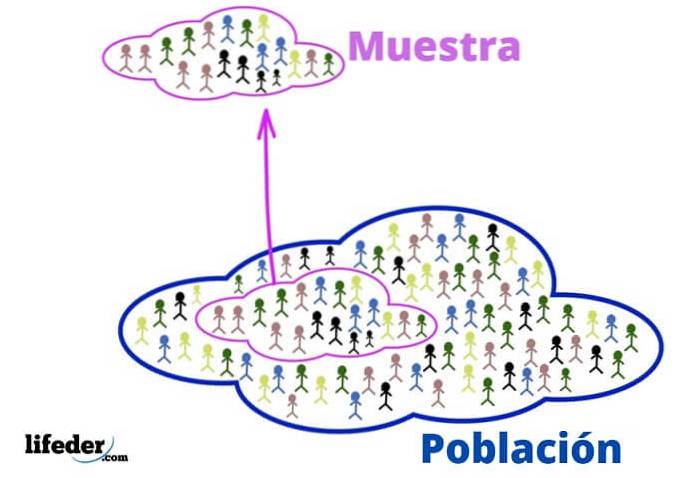
Befolkningen er det univers, som du vil studere. Det handler ikke nødvendigvis om mennesker eller levende væsener, da befolkningen i statistikker kan bestå af objekter eller ideer.
Prøven er for sin del en delmængde af populationen, der nøje udvindes fra den, fordi den er repræsentativ..
Prøveudtagning
Det er det sæt teknikker, hvormed en prøve udvælges fra en given population. Prøveudtagning kan være tilfældig, hvis probabilistiske metoder bruges til at vælge prøven eller ikke-probabilistisk, hvis analytikeren har sine egne udvælgelseskriterier, alt efter hans erfaring..
Statistiske variabler
Sæt af værdier, der kan have karakteristika for befolkningen. De klassificeres på forskellige måder, for eksempel kan de være diskrete eller kontinuerlige. Under hensyntagen til deres natur kan de også være kvalitative eller kvantitative..
Sandsynlighedsfordeling
Sandsynlighedsfunktioner, der beskriver adfærden for et stort antal systemer og situationer observeret i naturen. De mest kendte er den Gaussiske eller Gaussiske klokkefordeling og den binomiale distribution.
Parametre og statistik
Estimationsteorien fastslår, at der er et forhold mellem værdierne for befolkningen og værdierne for prøven taget fra denne population. Det parametre er de egenskaber ved befolkningen, som vi ikke kender, men som vi vil estimere: for eksempel middelværdien og standardafvigelsen.
For deres del Statistikker er prøvens egenskaber, for eksempel dens gennemsnit og standardafvigelse.
Antag som et eksempel, at befolkningen består af alle unge mellem 17 og 30 år i et samfund, og vi ønsker at kende andelen af dem, der i øjeblikket er i videregående uddannelse. Dette ville være populationsparameteren, der skal bestemmes.
For at estimere det vælges en tilfældig stikprøve på 50 unge, og andelen af dem, der studerer ved et universitet eller et højere læreanstal, beregnes. Denne andel er statistikken.
Hvis det efter undersøgelsen fastslås, at 63% af de 50 unge er i videregående uddannelse, er dette populationsestimatet, der er lavet ud fra stikprøven.
Dette er kun et eksempel på, hvad inferentiel statistik kan gøre. Det er kendt som estimering, men der er også teknikker til at forudsige statistiske variabler såvel som til at træffe beslutninger.
Statistisk hypotese
Det er en formodning, der gøres om værdien af middelværdien og standardafvigelsen for nogle karakteristika for befolkningen. Medmindre befolkningen undersøges fuldt ud, er dette ukendte værdier.
Hypotese testning
Er antagelserne om befolkningsparametre gyldige? For at finde ud af det verificeres det, om resultaterne fra prøven understøtter dem eller ej, så det er nødvendigt at designe hypotesetest.
Dette er de generelle trin til at udføre en:
Trin 1
Identificer typen af distribution, som befolkningen forventes at følge.
Trin 2
Angiv to hypoteser, betegnet som Heller og H1. Den første er nulhypotesen hvor vi antager, at parameteren har en bestemt værdi. Den anden er den alternative hypotese som antager en anden værdi end nulhypotesen. Hvis dette afvises, accepteres den alternative hypotese.
Trin 3
Opret en acceptabel margen for forskellen mellem parameteren og statistikken. Disse viser sig sjældent at være identiske, selvom de forventes at være meget tætte..
Trin 4
Foreslå et kriterium for at acceptere eller afvise nulhypotesen. Til dette anvendes en teststatistik, som kan være middelværdien. Hvis middelværdien er inden for visse grænser, accepteres nulhypotesen, ellers afvises den.
Trin 5
Som et sidste trin besluttes det, om nulhypotesen skal accepteres eller ej..
Temaer af interesse
Filialer af statistikker.
Statistiske variabler.
Befolkning og prøve.
Beskrivende statistik.
Referencer
- Berenson, M. 1985. Statistik for ledelse og økonomi, begreber og applikationer. Redaktionel Interamericana.
- Canavos, G. 1988. Sandsynlighed og statistik: Anvendelser og metoder. Mcgraw bakke.
- Devore, J. 2012. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. 8. plads Udgave. Cengage læring.
- Statistikhistorie. Gendannet fra: eumed.net.
- Ibañez, s. 2010. Matematik II. Kompetence tilgang. Cengage læring.
- Levin, R. 1981. Statistik for administratorer. Prentice hall.
- Walpole, R. 2007. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. Pearson.


Endnu ingen kommentarer