Det fraktioner eller brøktal er de tal, der er repræsenteret ved at angive kvotienten mellem to hele tal til Y b, så længe b er forskellig fra 0. For eksempel er 1/3 en brøkdel, der læses som "en tredjedel".
Til nummeret til det er kendt som tæller af fraktionen og til b Hvad nævneren Af det samme. Nævneren fortæller os, hvor mange dele der skal opdeles helheden i. Tælleren angiver for sin del, hvor mange dele af det hele der blev taget.
Det hele er alt, hvad du vil opdele eller dele, for eksempel en pizza eller chokoladestangen vist i figur 1. Stangen er lavet på en sådan måde, at det er meget let at opdele den i 5 lige store dele, hvor hver del er svarende til 1/5 af den fulde bjælke.
I brøkdelen eller brøktalet 1/5 er tælleren 1 og nævneren er 5. Brøken læses "en femtedel".
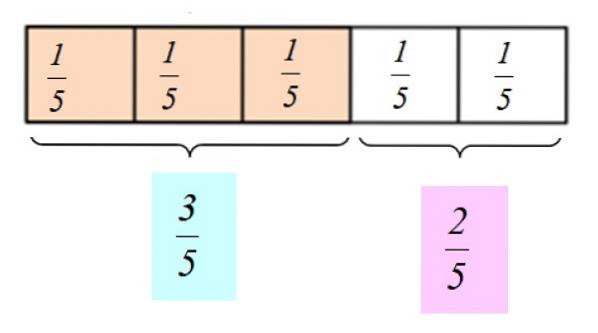
Antag, at vi spiser 3 stykker chokolade. Vi vil sige, at vi har spist 3/5 dele af baren, og der er 2/5 dele tilbage at dele med en ven. Vi kan også sige, at vi spiste "tre femtedele af chokoladen" og gav "to femtedele" til vores ven.
Den grafiske gengivelse af disse brøktal er som følger:
Artikelindeks
En brøkdel er korrekt, når tælleren er mindre end nævneren, og dens værdi er således mindre end 1. Fraktionerne i det foregående afsnit, i eksemplet med chokolade, er korrekte fraktioner..
Andre eksempler på korrekte fraktioner er: ½; 8/10; 3/4 og mere.
Tælleren for de ukorrekte brøker er større end tælleren. For eksempel hører 4/3, 8/5, 21/10 til denne kategori.
Disse fraktioner repræsenterer et helt tal. Blandt dem er 4/2, 10/5 og 27/3, da hvis vi ser nøje, giver resultatet af at dividere tælleren med nævneren af disse fraktioner et helt tal.
Således: 4/2 = 2, 10/5 = 2 og 27/3 = 9.
To fraktioner n / m og p / q er ækvivalente, når dividering af tæller efter nævneren giver den samme størrelse. På denne måde repræsenterer de ækvivalente fraktioner den samme del af helheden..
Som et eksempel har vi fraktionerne: 15/2 og 30/4. Når du deler 15 med 2, får du 7,5, men det er også det samme, hvis du deler 30 med 4.
For at finde ud af om to fraktioner n / m og p / q er ækvivalente, bekræftes følgende ligestilling:
n * q = smp
Når tælleren og nævneren deles med det samme tal og forudsat at resultatet er et heltal, opnås en brøk svarende til originalen, men med mindre tal.
Denne proces fortsætter, så længe tælleren og nævneren har nøjagtig samme skillevæg. Når det ikke er muligt at fortsætte med at dele, bliver irreducerbar fraktion af den oprindelige fraktion.
Fordelen ved at arbejde med den irreducerbare fraktion er, at der opnås en ækvivalent fraktion, men med mindre antal. Det er derfor, når du arbejder med brøker, skal du sørge for at reducere dem, når det er muligt, for at lette beregningerne..
Antag at fraktionen 12/20, idet den er tæller og nævneren jævn, kan begge deles med 2:
12/20 = 6/10
Og endnu en gang:
6/10 = 3/5
Fraktionen 3/5 svarer til 12/20, men enklere.
En forkert brøkdel indrømmer også repræsentation som et blandet tal, såkaldt fordi det har et heltal og en anden brøkdel, hvor brøkdelen er en ordentlig brøkdel..
Lad os se på et hurtigt eksempel med den brøkdel 15/2, som vi ved, er lig med 7,5.
Vi kan udtrykke 15/2 som et blandet tal som dette:
15/2 = 7 + 0,5
Men 0,5 = ½. Derfor er 15/2 = 7 ½, der lyder "syv og en halv".
Brøktal er nødvendige, fordi både naturlige og heltal er utilstrækkelige, når vi vil opdele ting som candy bar.
Og det er derfor, der er et uendeligt udvalg af målemønstre og objekter, hvis specifikationer inkluderer brøktal, for ikke at nævne antallet af hverdagssituationer, hvor disse er nødvendige..
I lande, hvor det metriske system anvendes, er det almindeligt at bruge kiloen til at henvise til vægten af mange fødevarer. Vi ønsker ikke altid at købe hele mængder, men lidt mere eller lidt mindre.
Derfor spørger vi:
Og når man bruger de angelsaksiske målestandarder, sker det samme: vi har brug for 2 og et halvt pund eller 1/4 pund af noget.
Alle disse tal er brøkdele og svarer, som vi har set, til to forskellige brøkstyper: korrekt og forkert..
Madlavningsopskrifter bruger ofte brøktal for at angive mængden af visse ingredienser. For eksempel:
Mål på møbler, tekstilstykker og alle slags husholdningsredskaber måles i brøkdele af en meter eller en tomme, uanset om de bruger det metriske eller angelsaksiske decimalsystem..
Selv i lande, hvor det metriske system er fremherskende, kommer kommercielle kobber-, stål- og andre VVS-rør ofte med diametre angivet i inches. Også anden hardware såsom skruer og møtrikker.
Da en tomme svarer til 2,54 cm, udtrykkes disse stykker, som har mindre diametre, normalt i fraktioner på en tomme..
Meget almindelige foranstaltninger til husrør er:
Brøktal bruges dagligt til at udtrykke tidsintervaller som ¼, ½ og ¾ på en time eller endda lidt længere: 1 time og ¼ og så videre.
I dag har Juanito bragt en kage til skolen til sin fødselsdag, og han vil distribuere den blandt alle sine venner, men han vil give læreren et stykke, der er tre gange større end børnenes.
Under hensyntagen til at der er 24 børn + læreren, som du vil give svarende til tre stykker, i hvor mange stykker skal du skære kagen??
Hvis Juanito kun ville distribuere kagen blandt sine venner, ville de hver have 1/24.
Men da han ønsker at give en del til læreren, og at stykket er tre gange større, bliver han nødt til at fordele kagen blandt 24 elever + 3 stykker til læreren. Med andre ord svarer hvert barn til 1/27 stykker og læreren til 3/27 stykker.
Derudover, hvis vi reducerer fraktionen 3/27, opnår vi, at læreren tager 1/9 af kagen.
En virksomhed med en chef og tre ansatte har € 6.000 i omsætning hver måned. Hvor mange penge har hver person, hvis chefen vil beholde halvdelen af det, han har tjent?
Hvis chefen ønsker at vinde halvdelen, bliver han nødt til at beholde 6000/2, hvilket tjener € 3000. Af de øvrige 3.000 €, der er tilbage, skal de tre ansatte distribuere. Således tjener hver medarbejder 3000/3, hvilket resulterer i € 1000.
Find den irreducible brøkdel af:
a) 12/18 og b) 4/11
I det første tilfælde bemærker vi, at både tælleren og nævneren er lige og delelige med 2. De er også delelige med 3, da 12 og 18 er multipla af denne figur..
Så vi kan forenkle brøken ved at dividere både tælleren og nævneren enten med 2 eller med 3, rækkefølgen er ligeglad.
Startende med at dividere med 2:
12/18 = 6/9
Nu bemærker vi, at både tælleren og nævneren af denne ækvivalente brøk er multipla af 3, så dividerer begge med denne figur:
6/9 = 2/3
Og da 2 og 3 er primtal, har de ikke længere nogen anden fælles skiller undtagen 1. Vi har nået den irreducerbare brøkdel.
Den største fælles divisor GCF for tælleren og nævneren kunne også have været beregnet. For 12 og 18:
GCF (12,18) = 6.
Og så divideres tælleren og nævneren med dette tal, hvilket svarer til at gøre det i etaper.
Her observerer vi, at 11 er et primtal, og dets delere er 1 og 11. For sin del indrømmer 4 4, 2 og 1 som delere. Bortset fra 1 har disse tal ikke en fælles skillevæg, og derfor er brøkdelen 4/11 er ureducerbar.
Angiv, hvilken der er den største brøkdel af hvert par:
a) ¾ og 5/4
b) 3/7 og 4/9
Når to positive fraktioner har samme nævner, jo større er den, der har større tæller. Derfor er 5/4 større, da 5> 3.
Hvis fraktionerne n / m og p / q har forskellige nævnere, og begge er positive, er sammenligningskriteriet som følger:
Hvis n.q> m. p, derefter n / m> p / q
En anden mulighed er at finde decimaludtrykket for hver brøk og sammenligne.
I henhold til det første kriterium: n = 3, m = 7, p = 4, q = 9. Derfor: n.q = 3 * 4 = 12 og smp = 7 * 4 = 28.
Ligesom 12< 28, ocurre que 3/7 < 4/9.
Eller vi udtrykker hver brøk som en decimal og opnår dette:
3/7 = 0.428571428… .
4/9 = 0.444444444 ... .
Ellipsen indikerer, at antallet af decimaler er uendeligt. Men dette er nok til at bekræfte, at det faktisk er 4/9> 3/7.
Endnu ingen kommentarer