
Kumulativ frekvensformel, beregning, fordeling, eksempler

Det kumulativ frekvens er summen af de absolutte frekvenser f, fra den laveste til den, der svarer til en bestemt værdi af variablen. Til gengæld er den absolutte frekvens det antal gange, en observation vises i datasættet.
Undersøgelsesvariablen skal naturligvis kunne sorteres. Og da den akkumulerede frekvens opnås ved at tilføje de absolutte frekvenser, viser det sig, at den akkumulerede frekvens indtil de sidste data skal falde sammen med summen af dem. Ellers er der en fejl i beregningerne.

Normalt betegnes den kumulative frekvens som Fjeg (eller undertiden njeg) for at skelne den fra den absolutte frekvens fjeg og det er vigtigt at tilføje en kolonne til den i tabellen, som dataene er organiseret med, kendt som hyppighedstabel.
Dette gør det blandt andet lettere at holde styr på, hvor mange data der blev talt op til en bestemt observation..
A Fjeg det er også kendt som absolut kumulativ frekvens. Hvis divideret med de samlede data, har vi relativ kumulativ frekvens, hvis endelige sum skal være lig med 1.
Artikelindeks
- 1 Formler
- 1.1 Andre akkumulerede frekvenser
- 2 Sådan får du den kumulative frekvens?
- 2.1 Sådan udfyldes hyppighedstabellen
- 2.2 Hyppighedstabel
- 3 Kumulativ frekvensfordeling
- 4 Eksempel
- 5 Foreslået øvelse
- 5.1 Svar
- 6 Referencer
Formler
Den kumulative frekvens for en given værdi af variablen Xjeg er summen af de absolutte frekvenser f af alle værdier, der er mindre end eller lig med den:
Fjeg = f1 + Fto + F3 +... fjeg
Ved at tilføje alle de absolutte frekvenser opnås det samlede antal data N, det vil sige:
F1 + Fto + F3 +…. + Fn = N
Den foregående operation er skrevet på en opsummeret måde ved hjælp af summeringssymbolet:
∑ Fjeg = N
Andre kumulative frekvenser
Følgende frekvenser kan også akkumuleres:
-Relativ frekvens: opnås ved at dividere den absolutte frekvens fjeg mellem de samlede data N:
Fr = fjeg / N
Hvis de relative frekvenser fra den laveste til den, der svarer til en bestemt observation, tilføjes, har vi kumulativ relativ hyppighed. Den sidste værdi skal være lig med 1.
-Procentdel kumulativ relativ hyppighed: den akkumulerede relative frekvens ganges med 100%.
F% = (fjeg / N) x 100%
Disse frekvenser er nyttige til at beskrive dataens opførsel, for eksempel når man finder målingerne af central tendens.
Sådan får du den kumulative frekvens?
For at opnå den akkumulerede frekvens er det nødvendigt at bestille dataene og organisere dem i en frekvenstabel. Fremgangsmåden illustreres i følgende praktiske situation:
-I en onlinebutik, der sælger mobiltelefoner, viste salgsrekorden for et bestemt brand i marts måned følgende værdier pr. Dag:
1; to; 1; 3; 0; 1; 0; to; 4; to; 1; 0; 3; 3; 0; 1; to; 4; 1; to; 3; to; 3; 1; to; 4; to; 1; 5; 5; 3
Variablen er antal solgte telefoner om dagen og det er kvantitativt. Dataene præsenteret på denne måde er ikke så lette at fortolke, for eksempel kan ejere af butikken være interesseret i at vide, om der er nogen tendens, såsom ugedage, hvor salget af det brand er højere..
Information som denne og mere kan opnås ved at præsentere dataene på en ordnet måde og angive frekvenserne..
Sådan udfyldes hyppighedstabellen
For at beregne den kumulative frekvens bestilles dataene først:
0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; to; to; to; to; to; to; to; to; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Derefter bygges en tabel med følgende oplysninger:
-Den første kolonne til venstre med antallet af solgte telefoner, mellem 0 og 5 og i stigende rækkefølge.
-Anden kolonne: absolut frekvens, hvilket er antallet af dage, hvor 0 telefoner, 1 telefon, 2 telefoner osv. Blev solgt.
-Tredje kolonne: den akkumulerede frekvens, der består af summen af den tidligere frekvens plus hyppigheden af de data, der skal overvejes.
Denne kolonne begynder med de første data i kolonnen med absolut frekvens, i dette tilfælde er den 0. For den næste værdi skal du tilføje denne med den forrige. Det fortsætter sådan, indtil det når de sidste data for den akkumulerede frekvens, som skal falde sammen med de samlede data.
Tabel over frecuency
Følgende tabel viser variablen "antal solgte telefoner på en dag", dens absolutte frekvens og den detaljerede beregning af dens akkumulerede frekvens.
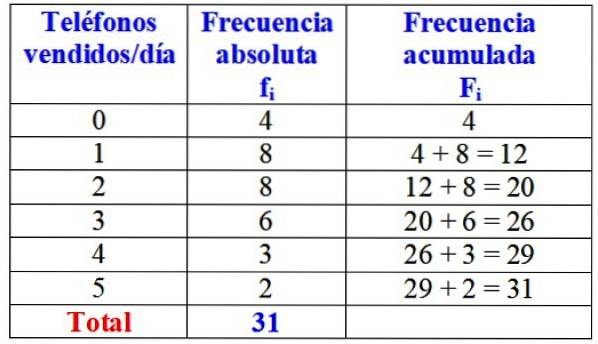
Ved første øjekast kan det siges, at af det pågældende mærke sælges en eller to telefoner næsten altid om dagen, da den højeste absolutte frekvens er 8 dage, hvilket svarer til disse værdier af variablen. Først i løbet af 4 dage i måneden solgte de ikke en enkelt telefon.
Som nævnt er tabellen lettere at undersøge end de individuelle data, der oprindeligt blev indsamlet.
Kumulativ frekvensfordeling
En kumulativ frekvensfordeling er en tabel, der viser de absolutte frekvenser, de kumulative frekvenser, de kumulative relative frekvenser og de kumulative procentfrekvenser..
Selv om der er fordelen ved at organisere dataene i en tabel som den foregående, hvis antallet af data er meget stort, er det måske ikke nok at organisere dem som vist ovenfor, for hvis der er mange frekvenser, bliver det stadig svært at fortolke.
Problemet kan løses ved at bygge en frekvensfordeling med intervaller, en nyttig procedure, når variablen tager et stort antal værdier, eller hvis det er en kontinuerlig variabel.
Her er værdierne grupperet i intervaller med lige amplitude, kaldet klasse. Klasserne er kendetegnet ved at have:
-Klassegrænse: er de ekstreme værdier for hvert interval, der er to, den øvre grænse og den nedre grænse. Generelt hører den øvre grænse ikke til intervallet, men til den næste, mens den nedre grænse hører hjemme.
-Klassemærke: er midtpunktet for hvert interval og tages som den repræsentative værdi af det.
-Klassebredde: Det beregnes ved at trække værdien af de største og mindste data (interval) og dividere med antallet af klasser:
Klassebredde = Område / antal klasser
Udarbejdelsen af frekvensfordelingen er beskrevet nedenfor..
Eksempel
Dette datasæt svarer til 40 karakterer af en matematikprøve på en skala fra 0 til 10:
0; 0; 0; 1; 1; 1; 1; to; to; to; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.
En frekvensfordeling kan foretages med et bestemt antal klasser, for eksempel 5 klasser. Man skal huske på, at dataene ikke er lette at fortolke, når man bruger mange klasser, og følelsen af at udføre grupperingen går tabt.
Og hvis de tværtimod er grupperet i meget få, så fortyndes informationen, og en del af den går tabt. Det hele afhænger af mængden af data, du har.
I dette eksempel er det en god idé at have to scores i hvert interval, da der er 10 scores og 5 klasser oprettes. Området er subtraktionen mellem den højeste og den laveste karakter, idet klassebredden er:
Klassebredde = (10-0) / 5 = 2
Intervallerne er lukket til venstre og åbne til højre (undtagen den sidste), hvilket er symboliseret med henholdsvis parenteser og parenteser. De har alle samme bredde, men det er ikke obligatorisk, selvom det oftest er.
Hvert interval indeholder en bestemt mængde elementer eller absolut frekvens, og i den næste kolonne er den akkumulerede frekvens, hvor summen bæres. Tabellen viser også den relative frekvens fr (absolut frekvens mellem det samlede antal data) og den procentvise relative frekvens fr × 100%.
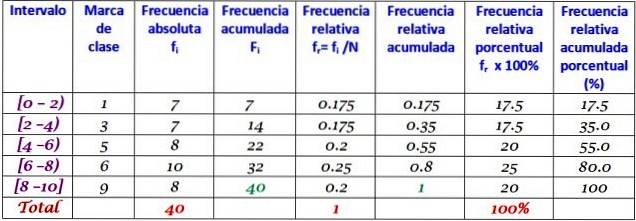
Foreslået øvelse
Et selskab foretog daglige opkald til sine kunder i årets første to måneder. Dataene er som følger:
6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7
Gruppér i 5 klasser, og opbyg tabellen med frekvensfordelingen.
Svar
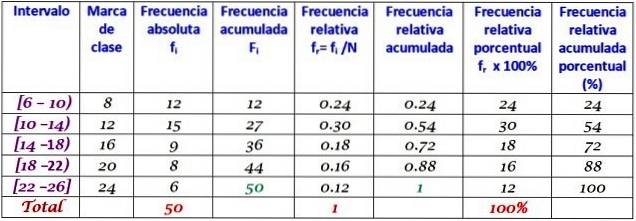
Klassebredden er:
(26-6) / 5 = 4
Prøv at finde ud af det, før du ser svaret.
Referencer
- Berenson, M. 1985. Statistik for ledelse og økonomi. Interamericana S.A.
- Devore, J. 2012. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. 8. plads Udgave. Cengage.
- Levin, R. 1988. Statistik for administratorer. 2. plads Udgave. Prentice hall.
- Sandsynlighed og statistik. Klasseintervalbredde. Gendannet fra: pedroprobabilidadyestadistica.blogspot.com.
- Spiegel, M. 2009. Statistik. Schaum-serien. 4. plads Udgave. Mcgraw bakke.
- Walpole, R. 2007. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. Pearson.


Endnu ingen kommentarer