
Dynamisk friktion eller kinetisk koefficient, eksempler, øvelser
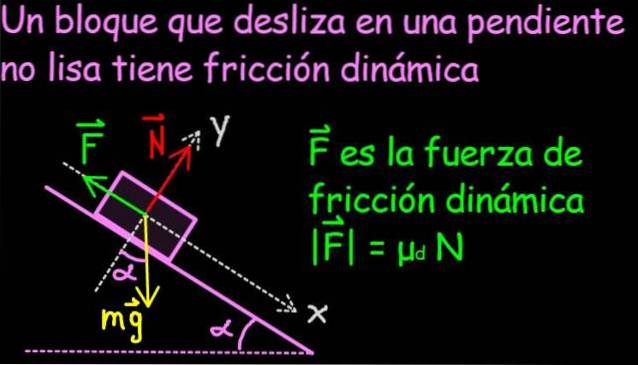
Det dynamisk friktion eller kinetisk Det er den, der forekommer mellem to kroppe i kontakt, når overfladen af den ene af dem bevæger sig i forhold til overfladen af den anden. For eksempel er friktionen i en kasse, der glider ned ad en hældning, dynamisk og fordeles over blokens kontaktflade.
Hældningen skal være stor nok til, at den tangentielle komponent af vægten er lig med eller overstiger friktionskraften, ellers vil den nedadgående blok ende med at stoppe.
Friktionskraften er yderst vigtig i det daglige liv, da den tillader bevægelse af mennesker, dyr og køretøjer. På en friktionsfri overflade, såsom en frossen sø, er det ikke muligt at starte bevægelse.
Friktion tillader også vores biler at stoppe, når de er i bevægelse.
Ved bremsning trykkes bremseklodser mod hjulskiverne, og takket være dynamisk friktion stopper de deres rotation. Men det er ikke nok at have gode bremser, det er nødvendigt, at der er nok friktionskraft mellem dækkene og jorden, for til sidst er dette den kraft, som vi er afhængige af for at få bilen til at stoppe..
Menneskeheden har lært at styre friktion til sin fordel. Således begyndte han med at bruge friktion mellem to stykker tørt træ til at skabe ild.
Naturen har også lært at håndtere friktion i sin favør. For eksempel er de synoviale membraner, der forer knoglerne i leddene, en af overfladerne med den laveste friktionskoefficient, der findes..
Artikelindeks
- 1 Koefficient for dynamisk friktion
- 1.1 Lov om dynamisk friktion
- 2 Sådan bestemmes koefficienten for dynamisk friktion?
- 2.1 Eksperiment
- 3 Tabel over friktionskoefficienten for nogle materialer
- 4 Øvelser
- 4.1 - Øvelse 1
- 4.2 - Øvelse 2
- 5 Referencer
Dynamisk friktionskoefficient
Leonardo da Vinci var den første til systematisk at studere bevægelsen af en blok, der glider på en plan overflade, men hans studier gik ubemærket hen.
Det var først i det 17. århundrede, at den franske fysiker Guillaume Amontons genopdagede friktionsloven:
Lov om dynamisk friktion
1.- Friktionskraften til stede i en blok, der glider på en plan overflade, modsætter sig altid bevægelsesretningen.
2.- Størrelsen af den dynamiske friktionskraft er proportional med fastspændingskraften eller den normale kraft mellem overfladerne på blokken og støtteplanet.
3.- Den proportionelle konstant er friktionskoefficienten, statisk μog i tilfælde af ingen glidning og dynamisk μd når der er. Friktionskoefficienten afhænger af overfladernes materialer i kontakt og ruhedstilstanden.
4. - Friktionskraften er uafhængig af det tilsyneladende kontaktområde.
5.- Når bevægelsen af den ene overflade i forhold til den anden begynder, er friktionskraften konstant og afhænger ikke af den relative hastighed mellem overfladerne.
I tilfælde af ingen glidning anvendes statisk friktion, hvis kraft er mindre end eller lig med den statiske friktionskoefficient ganget med det normale.
Den sidste ejendom var resultatet af bidraget fra den franske fysiker Charles Augustin de Coulomb, bedst kendt for sin berømte kraftlov mellem punkt elektriske ladninger..
Disse observationer fører os til den matematiske model for den dynamiske friktionskraft F:
F = μd N
Hvor μd er den dynamiske friktionskoefficient og N er den normale kraft.
Sådan bestemmes koefficienten for dynamisk friktion?
Koefficienten for dynamisk friktion mellem to overflader bestemmes eksperimentelt. Dens værdi afhænger ikke kun af materialerne på begge overflader, men af den ruhed eller polering, de har, samt deres renhed..
En måde at bestemme dette på er at skubbe og glide en kasse med kendt masse over en vandret overflade..
Hvis man kender hastigheden i det øjeblik, man kører frem, og afstanden fra det øjeblik til stoppet måles, er det muligt at kende bremseacceleration på grund af dynamisk friktion.
Eksperiment
I dette eksperiment måles starthastigheden v og afstanden d, derefter er bremseacceleration:
a = - vto / 2d
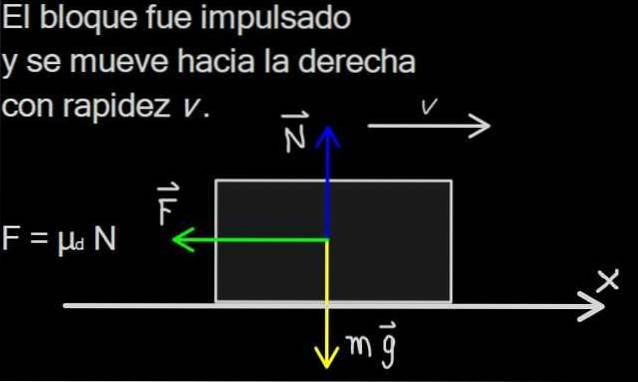
Kraftdiagrammet er vist i figur 2. Vægtens størrelse er massen m af blokken ganget med tyngdeaccelerationen g, og som kendt peger vægten altid lodret nedad..
N er den normale kraft på grund af den bærende overflades opadgående tryk og er altid vinkelret (eller normal) på planet. Normalet eksisterer, så længe overfladerne er i kontakt og ophører, så snart overfladerne adskilles.
Kraften F repræsenterer den dynamiske friktionskraft. Den fordeles faktisk på den nederste overflade af blokken, men vi kan repræsentere den som en enkelt kraft F anvendt i midten af blokken.
Da der er lodret ligevægt, er størrelsen af det normale N er lig med vægten af mg:
N = mg
I vandret retning forårsager friktionskraften deceleration af masseblokken m ifølge Newtons anden lov:
-F = m a
Friktionskraft F peger mod venstre, så dens vandrette komponent er negativ, m er blokens masse og a er bremseacceleration.
Det var tidligere opnået a = - vto / 2d og også den dynamiske friktionsmodel indikerer, at:
F = μd N
Ved at erstatte i den foregående ligning har vi:
-μd N = - vto / 2d
Under hensyntagen til at N = mg kan den dynamiske friktionskoefficient allerede løses:
μd = vto / (2d mg)
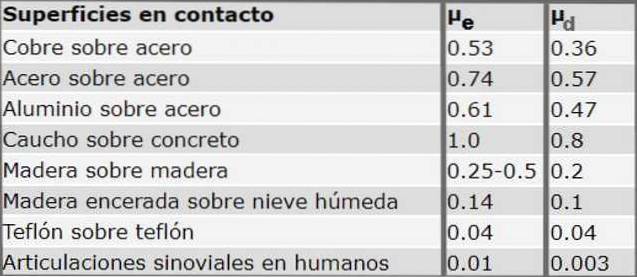
Tabel over friktionskoefficienten for nogle materialer
Den følgende tabel viser de statiske og dynamiske friktionskoefficienter for forskellige materialer. Det skal bemærkes, at systematisk er koefficienten for statisk friktion altid større end koefficienten for dynamisk friktion..
Uddannelse
- Øvelse 1
En blok på 2 kg masse skubbes på et vandret gulv og frigøres. I øjeblikket frigives registreres en hastighed på 1,5 m / s. Fra det øjeblik, indtil blokken stopper på grund af dynamisk friktion, køres der 3 m. Bestem koefficienten for kinetisk friktion.
Opløsning
Ifølge formlen opnået i eksemplet i det foregående afsnit er den dynamiske (eller kinetiske) friktionskoefficient:
μd = vto / (2d mg) = 1.5to / (2x3x2 x9,8) = 0,019.
- Øvelse 2
Ved at vide, at blokken i figur 1 falder ned med konstant hastighed, at blokens masse er 1 kg, og at planens hældning er 30 º, skal du bestemme:
a) Værdien af den dynamiske friktionskraft
b) Koefficienten for dynamisk friktion mellem blokken og planet.
Opløsning
I figur 4 er bevægelsesligningen (Newtons anden lov) vist for problemet med en blok, der falder ned ad en hældning med friktionskoefficient μd og hældning α (se kraftdiagram i figur 1)
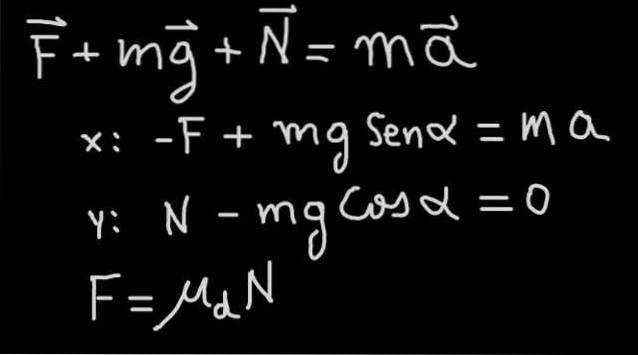
I vores øvelse får vi at vide, at blokken falder ned med konstant hastighed, derfor falder den ned med acceleration a = 0. Derfra følger det, at friktionskraften er sådan, at den er lig med den tangentielle komponent af vægten: F = mg Sen (α).
I vores tilfælde m = 1 kg og α = 30º, så friktionskraften F har en værdi på 4,9N.
På den anden side er den normale kraft N lig med og i modsætning til den lodrette komponent af vægten: N = mg Cos (α) = 8,48N .
Derefter følger det, at koefficienten for dynamisk friktion er:
μd = F / N = 4,9 N / 8,48 N = 0,57
Referencer
- Alonso M., Finn E. 1970. Fysik. Bind I. mekanik. Interamerikansk Uddannelsesfond S.A.
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Hewitt, P. 2012. Konceptuel fysik. Femte udgave.
- Rex, A. 2011. Grundlæggende fysik. Pearson.
- Serway R. 1992. Fysik. McGraw-Hill.
- Young, H. 2015. Universitetsfysik med moderne fysik. 14. udgave Pearson.


Endnu ingen kommentarer