EN bijektiv funktion er en, der opfylder den dobbelte betingelse for at være injektionsdygtig og surjektiv. Det vil sige, at alle elementerne i domænet har et enkelt billede i codomain, og til gengæld er codomain lig med funktionens rang ( RF ).
Det opfyldes ved at overveje et en-til-en-forhold mellem elementerne i domænet og codomain. Et simpelt eksempel er funktionen F: R → R defineret af linjen F (x) = x
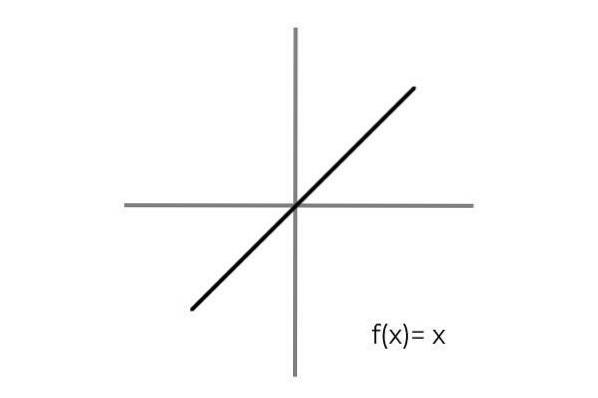
Det bemærkes, at der for hver værdi af domænet eller startsættet (begge termer gælder ens) er der et enkelt billede i kodomænet eller ankomstsættet. Derudover er der intet element i kodomænet, der ikke er et billede.
Dermed F: R → R defineret af linjen F (x) = x er bindende
Artikelindeks
For at besvare dette er det nødvendigt at være klar over de begreber, der henviser til Injektivitet Y Surjektivitet af en funktion, ud over kriterierne for at konditionere funktioner for at tilpasse dem til kravene.
En funktion er injektionsmiddel når hvert af elementerne i dets domæne er relateret til et enkelt element i kodomænet. Et element i codomain kan kun være billedet af et enkelt element i domænet, på denne måde kan værdierne for den afhængige variabel ikke gentages.
At overveje injektionsmiddel til en funktion skal følgende være opfyldt:
∀ x1 ≠ xto ⇒ F (x1 ) ≠ F (xto )
En funktion er klassificeret som overvejelse, hvis hvert element i dets kodomæne er et billede af mindst et element af domænet.
At overveje overvejelse til en funktion skal følgende være opfyldt:
Være F: DF → CF
∀ b ℮ CF OG til ℮ DF / F (a) = b
Dette er den algebraiske måde at fastslå, at for hver "b", der hører til CF der er et “a”, der tilhører DF sådan at funktionen evalueret i "a" er lig med "b".
Nogle gange en funktion, der ikke er bijective, det kan underkastes visse betingelser. Disse nye forhold kan gøre det til et bijektiv funktion. Alle former for ændringer af funktionens domæne og codomain er gyldige, hvor målet er at opfylde egenskaberne ved injektivitet og surjektivitet i det tilsvarende forhold..
Lad funktionen F: R → R defineret af linjen F (x) = 5x +1
A: [Alle reelle tal]
Det bemærkes, at for hver værdi af domænet er der et billede i kodomænet. Dette billede er unikt, hvilket gør F være en injektionsfunktion. På samme måde observerer vi, at kodens hoved for funktionen er lig med dens rang. Således opfylder betingelsen for surjectivity.
At være injektionsdygtig og surjectiv på samme tid kan vi konkludere
F: R → R defineret af linjen F (x) = 5x +1 er en bijektiv funktion.
Dette gælder for alle lineære funktioner (Funktioner hvis største grad af variablen er en).
Lad funktionen F: R → R defineret af F (x) = 3xto - to
Når man tegner en vandret linje, observeres det, at grafen findes ved mere end en lejlighed. På grund af dette funktionen F det er ikke injektionsdygtigt og vil derfor ikke være bijective så længe det er defineret i R → R
På samme måde er der værdier for codomain, der ikke er billeder af noget element i domænet. På grund af dette er funktionen ikke surjectiv, hvilket også fortjener at betingelsen for ankomstsættet.
Vi fortsætter med at betingelse for funktionens domæne og codomain
F: [0 , ∞] → [- to , ∞ ]
Hvor det observeres, at det nye domæne omfatter værdierne fra nul til positiv uendelighed. Undgå gentagelse af værdier, der påvirker injektionsevnen.
Ligeledes er codomain blevet ændret, tæller fra "-2" til positiv uendelighed, og eliminerer fra codomain de værdier, der ikke svarede til noget element i domænet
På denne måde kan det sikres, at F : [0 , ∞] → [- to , ∞ ] defineret af F (x) = 3xto - to
Det er bindende
Lad funktionen F: R → R defineret af F (x) = Sen (x)
I intervallet [ -∞ , +∞ ] sinusfunktionen varierer dens resultater mellem nul og en.
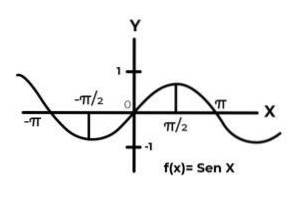
Funktionen F det svarer ikke til kriterierne for injektivitet og surjektivitet, fordi værdierne for den afhængige variabel gentages hvert interval på π. Også vilkårene for codomain uden for intervallet [ -elleve ] De er ikke et billede af noget element i domænet.
Når du studerer grafen for funktionen F (x) = Sen (x) intervaller observeres, hvor kurvens opførsel opfylder kriterierne for bijektivitet. Som for eksempel intervallet DF = [ π / 2,3π / 2 ] til domænet. Y CF = [-1, 1] til codomain.
Hvor funktionen varierer resulterer fra 1 til -1 uden at gentage nogen værdi i den afhængige variabel. Og på samme tid er codomain lig med de værdier, der anvendes af udtrykket Sen (x)
På denne måde funktionen F: [ π / 2,3π / 2 ] → [-1, 1] defineret af F (x) = Sen (x). Det er bijektivt
Angiv de nødvendige betingelser for DF og CF. Så udtrykket
F (x) = -xto være bijective.
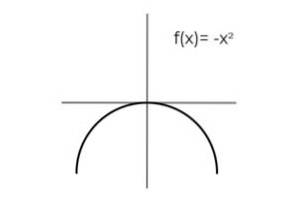
Gentagelse af resultater observeres, når variablen tager modsatte værdier:
F (2) = F (-2) = -4
F (3) = F (-3) = -9
F (4) = F (-4) = -16
Domænet er betinget og begrænser det til højre side af den rigtige linje.
DF = [0 , +∞ ]
På samme måde observeres det, at rækkevidden for denne funktion er intervallet [ -∞ , 0], som når de fungerer som et codomain opfylder betingelserne for surjectivity.
På denne måde kan vi konkludere det
Udtrykket F: [0 , +∞ ] → [ -∞ , 0] defineret af F (x) = -xto Det er bijektivt
Kontroller, om følgende funktioner er relevante:
F: [0 , ∞) → R defineret af F (x) = 3 (x + 1)to +to
F: [ 3π / 2,5π / 2 ] → R defineret af F (x) = 5ctg (x)
F: [ -π,π ] → R defineret af F (x) = Cos (x - 3)
F: R → R defineret af linjen F (x) = -5x + 4
Endnu ingen kommentarer