EN ideel gas eller perfekt gas Det er en, hvor den molekylære tiltrækning eller frastødningskraft mellem partiklerne, der sammensætter den, betragtes som ubetydelig, derfor er al dens indre energi kinetisk, det vil sige energi forbundet med bevægelse.
I en sådan gas er partiklerne normalt ret langt fra hinanden, skønt de fra tid til anden kolliderer med hinanden og med beholderens vægge..
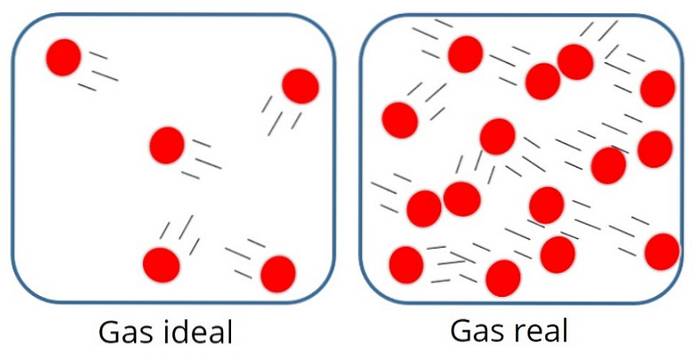
På den anden side betyder hverken størrelsen eller massen af partiklerne i den ideelle gas, da det antages, at det volumen, der er optaget af dem, er meget lille sammenlignet med selve gassen..
Dette er naturligvis kun en tilnærmelse, for i virkeligheden er der altid en vis grad af interaktion mellem atomer og molekyler. Vi ved også, at partikler optager plads og har masse..
Imidlertid fungerer disse antagelser ganske godt i mange tilfælde, såsom gasser med lav molekylvægt, i et godt område af tryk og temperaturer..
Gasser med høj molekylvægt, især ved høje tryk eller lave temperaturer, opfører sig imidlertid slet ikke som ideelle gasser og andre modeller skabt med det formål at beskrive dem med større præcision er nødvendige..
Artikelindeks
De love, der styrer gasser, er empiriske, dvs. de opstod fra eksperimentering. De mest bemærkelsesværdige eksperimenter blev udført gennem det syttende, attende og tidlige nittende århundrede.
For det første er Robert Boyle (1627-1691) og Edme Mariotte (1620-1684), der uafhængigt ændrede Tryk i en gas og registrerede dens ændring af bind, at finde ud af, at de var omvendt proportionale: jo højere tryk, jo mindre volumen.
For sin del fastslog Jacques Charles (1746-1823), at volumen og temperatur absolutte værdier var direkte proportionale, så længe trykket forblev konstant.
Amadeo Avogadro (1776-1856) opdagede, at to identiske volumener af forskellige gasser indeholdt det samme antal partikler, så længe tryk og temperatur var den samme. Og til sidst sagde Joseph de Gay Lussac (1778-1850), at ved at holde lydstyrken fast, er trykket i en gas direkte proportionalt med temperaturen..
Disse opdagelser udtrykkes i enkle formler, kaldende s til pres, V til volumen, n til antallet af partikler og T den ideelle gastemperatur:
Så længe temperaturen er fast, sker følgende:
p⋅V = konstant
Når gassen er under konstant tryk:
V / T = konstant
Ved at holde gassen på et fast volumen er det tilfreds med:
p / T = konstant
Identiske volumener af gas under samme tryk og temperaturforhold har det samme antal partikler. Derfor kan vi skrive:
V ∝ n
Hvor n er antallet af partikler og ∝ er symbolet på proportionalitet.
Den ideelle gasmodel beskriver en gas således, at:
-Når partiklerne interagerer, gør de det i meget kort tid ved hjælp af elastiske kollisioner, hvor momentum og kinetisk energi bevares..
-Dens bestanddele er punktlige, med andre ord deres diameter er meget mindre end den gennemsnitlige afstand, de bevæger sig mellem en kollision og en anden..
-Intermolekylære kræfter findes ikke.
-Kinetisk energi er proportional med temperaturen.
Monatomiske gasser - hvis atomer ikke er bundet sammen - og lav molekylvægt under standardbetingelser for tryk og temperatur (atmosfærisk tryk og 0 ° C temperatur) har en sådan adfærd, at den ideelle gasmodel er en meget god beskrivelse for dem..
Ovennævnte gaslove kombineres for at danne den generelle ligning, der styrer opførelsen af den ideelle gas:
V ∝ n
V ∝ T
Derfor:
V ∝ n⋅T
Også fra Boyles lov:
V = konstant / s
Så vi kan bekræfte, at:
V = (konstant x n⋅T) / p
Konstanten kaldes gaskonstant og er betegnet med bogstavet R. Med dette valg relaterer den ideelle gasligning af tilstand fire variabler, der beskriver tilstanden for gassen, nemlig n, R, p og T, hvilket efterlader:
p⋅V = n⋅R⋅T
Denne relativt enkle ligning er i overensstemmelse med de ideelle gaslove. For eksempel, hvis temperaturen er konstant, reduceres ligningen til Boyle-Mariotte-loven.
Som vi har sagt før, under standardbetingelser for temperatur og tryk, dvs. ved 0 ° C (273,15 K) og 1 trykatmosfære, er adskilligheden af mange gasser tæt på den for den ideelle gas. Under disse betingelser er volumenet på 1 mol af gassen 22.414 L.
I det tilfælde:
R = (p⋅V) / (n⋅T) = (1 atm x 22,414 L) / (1 mol x 273,15 K) = 0,0821 atm ⋅ L / mol ⋅ K
Gaskonstanten kan også udtrykkes i andre enheder, for eksempel i SI International System er det værd:
R = 8,314 J3 mol-1⋅ K-1
Når man løser et problem ved hjælp af den ideelle gaslov, er det praktisk at være opmærksom på de enheder, hvori konstanten udtrykkes, da der som vi kan se, er der mange muligheder.
Som vi har sagt, opfører enhver gas under standardbetingelser for tryk og temperatur, og som har lav molekylvægt, meget tæt på den ideelle gas. Derfor er ligningen p⋅V = n⋅R⋅T anvendelig til at finde forholdet mellem de fire variabler, der beskriver det: n, p, V og T.
På denne måde kan vi forestille os en del af ideel gas indesluttet i en beholder og dannet af små partikler, der fra tid til anden kolliderer med hinanden og med beholderens vægge, altid elastisk..
Dette er hvad vi ser i den følgende animation af en del af helium, en monatomisk ædelgas:
En ideel gas er en hypotetisk gas, det vil sige, det er en idealisering, men i praksis opfører mange gasser sig meget tæt, hvilket gør det muligt for modellen p⋅V = n⋅R arroT at give meget gode resultater..
Eksempler på gasser, der opfører sig som ideelle under standardbetingelser, er ædelgasser såvel som lette gasser: brint, ilt og nitrogen..
Karls lov kan anvendes på varmluftballonen i figur 1: gassen varmes op, derfor ekspanderer luften, der fylder ballonen, og som en konsekvens stiger den.
Helium er sammen med brint det mest almindelige element i universet, og alligevel er det sjældent på jorden. Da det er en ædelgas, er den inert i modsætning til brint, hvorfor heliumfyldte balloner i vid udstrækning bruges som dekorative elementer..
Endnu ingen kommentarer