
Heptadecagon egenskaber, diagonaler, omkreds, areal

Det heptadecagon er en regelmæssig polygon med 17 sider og 17 hjørner. Dens konstruktion kan udføres i euklidisk stil, dvs. kun ved hjælp af linealen og kompasset. Det var det store matematiske geni Carl Friedrich Gauss (1777-1855), knap 18 år gammel, der fandt proceduren for dets konstruktion i 1796.
Tilsyneladende var Gauss altid meget tilbøjelig til denne geometriske figur i en sådan grad, at han fra den dag, han opdagede dens konstruktion, besluttede at være matematiker. Det siges også, at han ønskede, at heptadecagonen skulle være indgraveret på hans gravsten.

Gauss fandt også formlen til at bestemme, hvilke regelmæssige polygoner der har mulighed for at blive konstrueret med lineal og kompas, da nogle ikke har nøjagtig euklidisk konstruktion.
Artikelindeks
- 1 Karakteristika for heptadecagon
- 2 diagonaler og omkreds
- 2.1 Heptadagonens omkreds
- 3 Område
- 3.1 Areal givet side
- 3.2 Areal givet radius
- 4 eksempler
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 5 Referencer
Heptadecagonens egenskaber
Som for dens egenskaber, som enhver polygon, er summen af dens indre vinkler vigtig. I en regelmæssig polygon af n sider, summen er givet af:
Sa (n) = (n -2) * 180º.
For heptadecagon antallet af sider n det er 17, hvilket betyder, at summen af dens indre vinkler er:
Sa (17) = (17 - 2) * 180º = 15 * 180º = 2700º.
Denne sum, udtrykt i radianer, ser sådan ud:
Sa (17) = (17 - 2) * π = 15 * π = 15π
Fra ovenstående formler kan det let udledes, at hver indre vinkel i en heptadecagon har et nøjagtigt mål α givet ved:
α = 2700º / 17 = (15/17) π radianer
Det følger heraf, at den indvendige vinkel i omtrentlig form er:
α ≈ 158.824º
Diagonaler og omkreds
Diagonaler og omkreds er andre vigtige aspekter. I enhver polygon er antallet af diagonaler:
D = n (n - 3) / 2 og i tilfælde af heptadecagon, som n = 17, det er så det D = 119 diagonaler.
På den anden side, hvis længden af hver side af heptadecagon er kendt, så findes omkredsen af den almindelige heptadecagon simpelthen ved at tilføje 17 gange længden, eller hvad der svarer til 17 gange længden d På hver side:
P = 17 d
Heptadecagonens omkreds
Nogle gange er kun radius kendt r af heptadecagon, så det er nødvendigt at udvikle en formel til denne sag.
Til dette formål begrebet apotem. Apotemet er det segment, der går fra midten af den almindelige polygon til midtpunktet på den ene side. Apotemet i forhold til den ene side er vinkelret på den side (se figur 2).
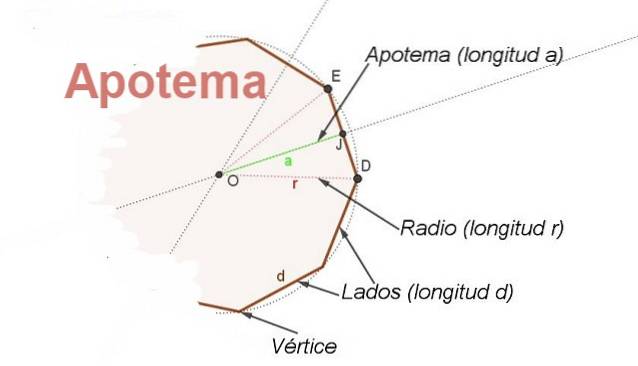
Derudover er apotemet halveringspunktet for vinklen med det centrale hjørne og siderne på to på hinanden følgende hjørner af polygonen, dette gør det muligt at finde et forhold mellem radius r og siden d.
Hvis det kaldes β til den centrale vinkel DOE og under hensyntagen til, at apotemet EFT er en bisector, du har EJ = d / 2 = r Sen (β / 2), hvorfra der er en relation til at finde længden d på siden af en kendt polygon er dens radius r og dens centrale vinkel β:
d = 2 r Sen (β / 2)
I tilfælde af heptadecagon β = 360º / 17 så du har:
d = 2 r Sen (180º / 17) ≈ 0,3675 r
Endelig opnås formlen for omkredsen af heptadecagon, kendt sin radius:
P = 34 r Sen (180º / 17) ≈ 6,2475 r
Omkredsen af en heptadecagon er tæt på omkredsen af omkredsen, der omgiver den, men dens værdi er mindre, det vil sige omkredsen af den omskrevne cirkel er Pcir = 2π r ≈ 6,2832 r.
Areal
For at bestemme området på heptadecagonen henviser vi til figur 2, der viser siderne og apotemet af en regelmæssig polygon af n sider. I denne figur er trekanten EOD har et areal svarende til basen d (polygonside) gange højde til (polygon apotem) divider med to:
EOD-område = (d x a) / 2
Så kendt apotemet til af heptadecagon og siden d dens område er:
Heptadecagon-område = (17/2) (d x a)
Området får siden
For at opnå en formel for området på heptadecagonen, der kender længden af dens sytten sider, er det nødvendigt at opnå en sammenhæng mellem længden af apotemet til og siden d.
Med henvisning til figur 2 opnås følgende trigonometriske forhold:
Tan (β / 2) = EJ / OJ = (d / 2) / a, være β til den centrale vinkel DOE. Så apotemet til kan beregnes, hvis længden er kendt d fra siden af polygonen og den centrale vinkel β:
a = (d / 2) Cotan (β / 2)
Hvis dette udtryk nu erstattes af apotemet, i formlen for området af heptadecagon opnået i det foregående afsnit, har vi:
Heptadecagon-område = (17/4) (dtoCotan (β / 2)
At være β = 360º / 17 til heptadecagon, så vi har endelig den ønskede formel:
Heptadecagon-område = (17/4) (dto) Cotan (180º / 17)
Område givet radius
I de foregående afsnit var der fundet et forhold mellem siden d af en regelmæssig polygon og dens radius r, idet dette forhold var følgende:
d = 2 r Sen (β / 2)
Dette udtryk for d introduceres i udtrykket opnået i det foregående afsnit for området. Hvis de relevante substitutioner og forenklinger foretages, opnås formlen, der gør det muligt at beregne arealet af heptadecagon:
Heptadecagon-område = (17/2) (rtoSen (β) = (17/2) (rtoSen (360º / 17)
Et omtrentligt udtryk for området er:
Heptadecagon-område = 3,0706 (rto)
Som forventet er dette område lidt mindre end det område af cirklen, der afgrænser heptadecagon. TILca. = π rto ≈ 3.1416 rto. For at være præcis er den 2% mindre end den af dens omskrevne cirkel.
Eksempler
Eksempel 1
Hvilken værdi skal radius og diameter for den omskrevne omkreds have for en heptadagon at have sider på 2 cm? Find også værdien af omkredsen.
For at besvare spørgsmålet er det nødvendigt at huske forholdet mellem siden og radius af en almindelig n-sidet polygon:
d = 2 r Sen (180º / n)
Til heptadecagon n = 17, så det d = 0,3675 r, heptadecagons radius er r = 2 cm / 0,3675 = 5,4423 cm eller
10,8844 cm diameter.
Omkredsen af en 2 cm sideheptadagon er P = 17 * 2 cm = 34 cm.
Eksempel 2
Hvad er arealet af en almindelig heptadecagon med en side på 2 cm?
Vi skal henvise til formlen vist i det foregående afsnit, som giver os mulighed for at finde arealet af en heptadecagon, når den har længden d på din side:
Heptadecagon-område = (17/4) (dto) / Tan (180º / 17)
Ved udskiftning d = 2 cm i ovenstående formel får du:
Areal = 90,94 cm
Referencer
- C. E. A. (2003). Geometrielementer: med kompasets øvelser og geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Opdag polygoner. Benchmark Education Company.
- Hendrik, V. (2013). Generelle polygoner. Birkhäuser.
- IGER. (s.f.). Matematik Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende udgave). Pearson Uddannelse.
- Patiño, M. (2006). Matematik 5. Redaktionel Progreso.
- Sada, M. 17-sidet regelmæssig polygon med lineal og kompas. Gendannet fra: geogebra.org
- Wikipedia. Heptadecagon. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer