Det Faradays lov i elektromagnetisme hedder det, at en skiftende magnetfeltstrøm er i stand til at inducere en elektrisk strøm i et lukket kredsløb.
I 1831 eksperimenterede den engelske fysiker Michael Faraday med at bevæge ledere inden for et magnetfelt og også variere magnetfelter, der passerede gennem faste ledere..
Faraday indså, at hvis han varierede magnetfeltstrømmen over tid, var han i stand til at etablere en spænding, der var proportional med denne variation. Hvis ε er spændingen eller den inducerede elektromotoriske kraft (induceret emf) og Φ er magnetfeltstrømmen, kan den i matematisk form udtrykkes:
| ε | = ΔΦ / Δt
Hvor symbolet Δ angiver variation i mængden, og bjælkerne i emf angiver den absolutte værdi af dette. Da det er et lukket kredsløb, kan strømmen strømme i den ene eller den anden retning.
Magnetisk flux, produceret af et magnetfelt over en overflade, kan variere på en række måder, for eksempel:
-Flytning af en stangmagnet gennem en cirkulær sløjfe.
-Forøgelse eller formindskelse af intensiteten af magnetfeltet, der passerer gennem sløjfen.
-Efterlader feltet fast, men ved hjælp af en eller anden mekanisme ændre området af sløjfen.
-Kombination af ovenstående metoder.
Artikelindeks
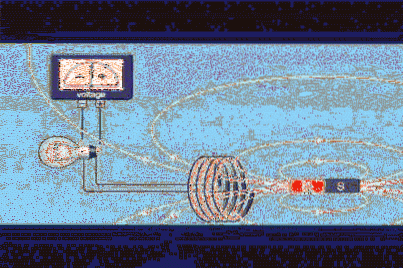
Antag at du har et lukket kredsløb af område A, såsom en cirkulær sløjfe eller en vikling svarende til den i figur 1, og at du har en magnet, der producerer et magnetfelt B.
Magnetfeltstrømmen Φ er en skalar størrelse, der refererer til antallet af feltlinjer, der krydser område A. I figur 1 er de hvide linjer, der forlader magnetens nordpol og vender tilbage mod syd.
Feltets intensitet vil være proportional med antallet af linjer pr. Arealeenhed, så vi kan se, at det ved polerne er meget intens. Men vi kan have et meget intenst felt, der ikke producerer flux i sløjfen, hvilket vi kan opnå ved at ændre orienteringen af denne (eller magneten).
For at tage højde for orienteringsfaktoren defineres magnetfeltstrømmen som det skalære produkt mellem B Y n, være n enhedens normale vektor til overfladen af sløjfen, og det angiver dens retning:
Φ = B•n A = BA.cosθ
Hvor θ er vinklen mellem B Y n. Hvis for eksempel B Y n er vinkelrette, magnetfeltstrømmen er nul, fordi i så fald er feltet tangent til sløjfens plan og ikke kan passere gennem overfladen.
I stedet for ja B Y n er parallelle, betyder det, at feltet er vinkelret på sløjfens plan, og linjerne passerer gennem det så vidt muligt.
Enheden i det internationale system for F er weberen (W), hvor 1 W = 1 T.mto (læs "tesla per kvadratmeter").
I figur 1 kan vi se, at spændingens polaritet ændres, når magneten bevæger sig. Polariteten er etableret ved Lenzs lov, der siger, at den inducerede spænding skal modsætte sig den variation, der producerer den.
Hvis for eksempel den magnetiske flux, der produceres af magneten, øges, etableres en strøm i lederen, der cirkulerer og skaber sin egen flux, som modsætter sig denne stigning..
Hvis tværtimod den flux, der skabes af magneten, falder, cirkulerer den inducerede strøm på en sådan måde, at dens egen flux modvirker faldet..
For at tage dette fænomen i betragtning placeres et negativt tegn foran Faradays lov, og det er ikke længere nødvendigt at placere de absolutte værdistænger:
ε = -ΔΦ / At
Dette er Faraday-Lenz-loven. Hvis strømningsvariationen er uendelig, erstattes deltas med forskelle:
ε = -dΦ / dt
Ovenstående ligning er gyldig for en sløjfe. Men hvis vi har en spole med N-drejninger, er resultatet meget bedre, fordi emf multipliceres N gange:
ε = - N (dΦ / dt)
For at strømmen skal tænde den pære, der skal produceres, skal der være relativ bevægelse mellem magneten og sløjfen. Dette er en af måderne, hvorpå fluxen kan variere, fordi på denne måde ændres intensiteten af det felt, der passerer gennem sløjfen..
Så snart magnetens bevægelse ophører, slukkes pæren, selvom magneten er stille i midten af sløjfen. Hvad der er nødvendigt for at cirkulere den strøm, der tænder pæren, er, at feltstrømmen varierer.
Når magnetfeltet varierer med tiden, kan vi udtrykke det som:
B = B (t).
Ved at holde området A på sløjfen konstant og lade det være fast i en konstant vinkel, som for figuren er 0º, så:
Hvis det er muligt at ændre området af sløjfen, lade dens orientering være fast og placere den midt i et konstant felt, gives den inducerede emk ved:
En måde at opnå dette på er at placere en stang, der glider på en lederskinne med en bestemt hastighed, som vist i den følgende figur.
Stangen og skinnen plus en pære eller en modstand forbundet med ledende ledninger danner et lukket kredsløb i form af en rektangulær sløjfe..
Når du skubber stangen, længden x øges eller formindskes, og med det ændres sløjfens område, hvilket er nok til at skabe en variabel strømning.
Som vi sagde før, hvis vinklen mellem B og det normale af sløjfen er lavet til at variere, feltstrømmen ændres efter:
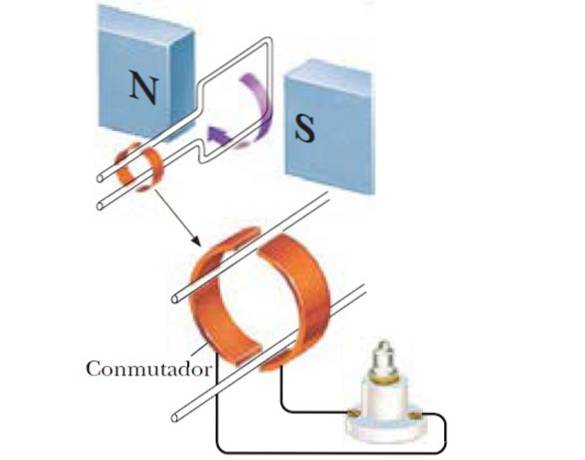
Således opnås en sinusformet generator, og hvis der i stedet for en enkelt spole anvendes et antal N spoler, er den inducerede emf større:
En cirkulær spole med N drejer og radius R, roterer med vinkelfrekvensen ω midt i et magnetfelt af størrelse B. Find et udtryk for den maksimale emf induceret i spolen.
Udtrykket for emf induceret af rotation anvendes når spolen har N drejer, velvidende at:
-Arealet af spolen er A = πRto
-Vinklen θ varierer som en funktion af tiden som θ = ωt
Det er vigtigt at bemærke, at først θ = ω erstattes i Faradays lov og snart er afledt med hensyn til tid:
ε = -NBA (cos θ) '= -NB (πRto[cos (ωt)] '= NBω (πRto) synd (ωt)
Da der kræves maksimum emf, sker det når sin ωt = 1, så til sidst:
εmaks = NBω (πRto)
Endnu ingen kommentarer