
Omtrentlig måling af eksempler på amorfe tal og motion
Det omtrentlig måling af amorfe figurer består af en række metoder, der bruges til at bestemme arealet eller omkredsen af geometriske figurer, der ikke er trekanter, firkanter, cirkler osv. Nogle kan udvides til tredimensionelle figurer.
Grundlæggende består målingen i at skabe et gitter med en eller anden regelmæssig form, såsom rektangler, firkanter eller trapezoider, der omtrent dækker overfladen. Præcisionen for arealtilnærmelsen opnået ved disse metoder øges med gitterets finhed eller tæthed..

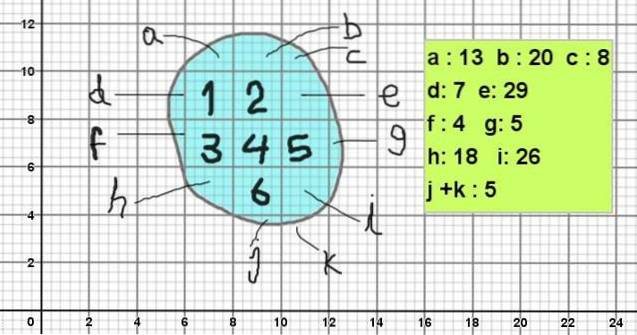
Figur 1 og 2 viser forskellige amorfe figurer. For at beregne arealet er der lavet et gitter bestående af 2 X 2 firkanter, som igen er opdelt i 25 2/5 x 2/5 firkanter.
Tilføjelse af arealerne på de vigtigste firkanter og de sekundære firkanter giver det omtrentlige areal af den amorfe figur.
Artikelindeks
- 1 Areal under en kurve
- 1.1 Regelmæssige intervaller
- 2 Eksempel
- 3 Øvelse løst
- 4 Referencer
Areal under en kurve
Det er ofte nødvendigt groft at beregne arealet under en kurve mellem to grænseværdier. I dette tilfælde kan der i stedet for et kvadratisk gitter tegnes rektangulære striber, der groft dækker området under kurven..
Summen af alle de rektangulære striber kaldes sum eller Riemann sum. Figur 3 viser en skillevæg af intervallet [a, b], hvor vi vil tilnærme området under kurven.
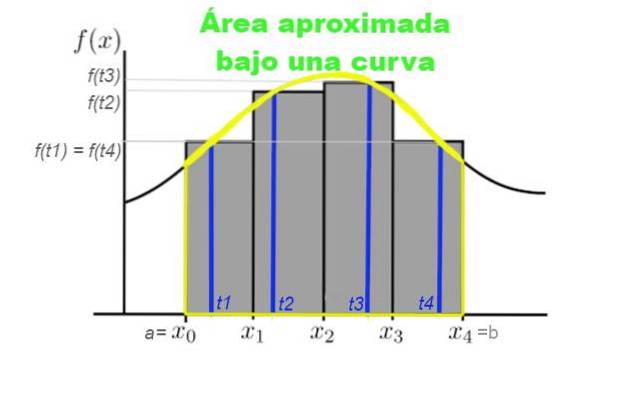
Antag at du vil beregne arealet under kurven givet af funktionen y = f (x), hvor x hører til intervallet [a, b] inden for hvilket du vil beregne området. Til dette laves en partition af n-elementer inden for dette interval:
Partition = x0 = a, x1, x2,…, xn = b.
Derefter opnås det omtrentlige areal under kurven givet af y = f (x) i intervallet [a, b] ved at udføre følgende summering:
S = ∑k = 1n f (tk) (xk - xk-1)
Hvor Tk er mellem xk-1 og xk: xk-1 ≤ tk ≤ xk .
Figur 3 viser grafisk Riemann-summen af kurven y = f (x) i intervallet [x0, x4]. I dette tilfælde blev der foretaget en opdeling af fire underintervaller, og summen repræsenterer det samlede areal af de grå rektangler.
Denne sum repræsenterer en tilnærmelse til arealet under kurven f mellem abscissen x = x0 og x = x4.
Tilnærmelsen til området under kurven forbedres som antallet n af skillevægge er større og har tendens til at være nøjagtigt området under kurven, når antallet n af skillevægge har en tendens til uendelig.
Hvis kurven er repræsenteret af en analytisk funktion, er værdierne f (tk) beregnes ved at evaluere denne funktion til t-værdiernek. Men hvis kurven ikke har et analytisk udtryk, forbliver følgende muligheder:
- Anslå kurven med en funktion, for eksempel et polynom.
- Tag de kartesiske koordinater for de punkter, hvor kurven krydser linierne x = tk.
Regelmæssige intervaller
Afhængig af valget af værdien tk i intervallet [xk, xk-1], kan summen overvurdere eller undervurdere den nøjagtige værdi af området under kurven for funktionen y = f (x). Det mest tilrådelige er at tage det punkt tk, hvor det manglende område er omtrent lig med det overskydende areal, selvom det ikke altid er muligt at træffe et sådant valg..
Tag tk yderst til højre
Det mest praktiske er derefter at bruge regelmæssige intervaller med bredde Δx = (b - a) / n, hvor a og b er minimums- og maksimumværdierne for abscissen, mens n er antallet af underinddelinger.
I så fald tilnærmes arealet under kurven med:
Areal = f (a + Δx) + f (a + 2Δx) +… + f [a + (n-1] Δx + f (b) * Δx
I ovenstående udtryk blev tk taget i højre ende af underintervallet.
Tag tk yderst til venstre
En anden praktisk mulighed er at tage værdien tk yderst til venstre, i hvilket tilfælde summen, der tilnærmer området, udtrykkes som:
Areal = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx)] * Δx
Tag tk som central værdi
Hvis tk vælges som den centrale værdi af det regelmæssige underinterval for bredden Δx, er summen, der tilnærmer sig området under kurven:
Areal = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx
Ethvert af disse udtryk har en tendens til den nøjagtige værdi i det omfang, at antallet af underinddelinger er vilkårligt stort, det vil sige, at Δx har en tendens til nul, men i dette tilfælde bliver antallet af termer i opsummeringen uhyre stort med de deraf følgende beregningsomkostninger.
Eksempel
Figur 2 viser en amorf figur, hvis kontur svarer til stenene i billede 1. For at beregne dens areal placeres den på et gitter med hovedkvadrater på 2 x 2 kvadratiske enheder (for eksempel kan de være 2 cm²)..
Og da hver firkant er opdelt i 5 x 5 underinddelinger, så har hver underafdeling et areal på 0,4 x 0,4 kvadratiske enheder (0,16 cm²).
Arealet på figuren beregnes således:
Areal = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²
Nemlig:
Areal = 12 cm² + 135 x 0,16 cm² = 33,6 cm².
Træning løst
Beregn omtrent arealet under kurven givet af funktionen f (x) = xto mellem a = -2 til b = +2. For at gøre dette skal du først skrive summen for n regelmæssige partitioner af intervallet [a, b] og derefter tage den matematiske grænse for det tilfælde, at antallet af partitioner har en tendens til uendelig.
Opløsning
Først definerer du intervallet for partitionerne som
Δx = (b - a) / n.
Derefter ser den rigtige sum svarende til funktionen f (x) sådan ud:


[-2 + (4i / n)]to = 4 - 16 i / n + (4 / n)to jegto
Og så erstattes det i summeringen:



Og det tredje resultat:

S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6nto
At vælge en stor værdi for n giver en god tilnærmelse til arealet under kurven. I dette tilfælde er det dog muligt at få den nøjagtige værdi ved at tage den matematiske grænse, når n har tendens til uendelig:
Areal = limn-> ∞[16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6nto]
Areal = 16 - (64/2) + (64/3) = 16/3 = 5.333.
Referencer
- Casteleiro, J. M. 2002. Integral calculus (Illustreret udgave). Madrid: ESIC Editorial.
- Larson, R. 2010. Beregning af en variabel. 9. Udgave. Mcgraw bakke.
- Purcell, E. 2007. Calculus med analytisk geometri. 9. Udgave. Pearson Uddannelse.
- Unican. Historien om begrebet integral. Gendannet fra: repositorio.unican.es
- UIS. Summer Riemann. Gendannet fra: matematicas.uis.edu.co
- Wikipedia. Areal. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer