Mål for variabilitet

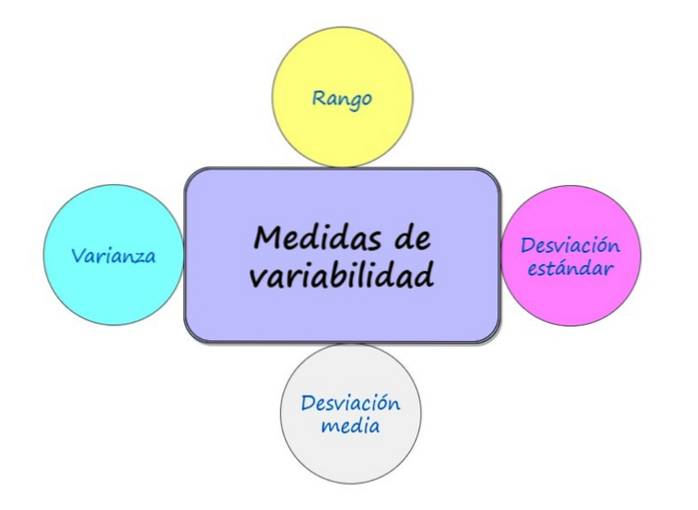
Hvad er mål for variabilitet?

Det målinger af variation, Også kaldet måling af spredning, de er statistiske indikatorer, der indikerer, hvor tæt eller langt dataene er fra dets aritmetiske gennemsnit. Hvis dataene er tæt på middelværdien, er fordelingen koncentreret, og hvis de er langt væk, er det en sparsom fordeling..

Der er mange målinger af variation, blandt de bedst kendte er:

• Rang
• Gennemsnitlig afvigelse
• Variation
• Standardafvigelse

Disse foranstaltninger supplerer målene for central tendens og er nødvendige for at forstå fordelingen af ​​de opnåede data og udtrække så mange oplysninger fra dem som muligt..

Rang

Område eller rækkevidde måler bredden af ​​et datasæt. For at bestemme dens værdi er forskellen mellem data med den højeste værdi x_maks og den med den laveste værdi x_min:

R = x_maks - x_min

Hvis dataene ikke er løse, men grupperet efter interval, beregnes området af forskellen mellem den øvre grænse for det sidste interval og den nedre grænse for det første interval.

Når området er en lille værdi, betyder det, at alle data er ret tæt på hinanden, men et stort interval indikerer, at der er meget variation. Det er klart, at bortset fra den øvre grænse og den nedre grænse for dataene ikke området tager højde for værdierne mellem dem, så det anbefales ikke at bruge det, når antallet af data er stort.

Det er dog en øjeblikkelig foranstaltning at beregne og har de samme dataenheder, så det er let at fortolke.

Eksempel på rækkevidde

Nedenfor er listen med antallet af scorede mål i weekenden i fodboldligaerne i ni lande:

40, 32, 35, 36, 37, 31, 37, 29, 39

Dette er et ikke-grupperet datasæt. For at finde rækkevidden fortsætter vi med at bestille dem fra laveste til højeste:

29, 31, 32, 35, 36, 37, 37, 39, 40

Dataene med den højeste værdi er 40 mål, og den med den laveste værdi er 29 mål, og derfor er intervallet:

R = 40−29 = 11 mål.

Det kan overvejes, at rækkevidden er lille sammenlignet med minimumsværdidataene, som er 29 mål, så det kan antages, at dataene ikke har stor variation.

Gennemsnitlig afvigelse

Dette mål for variabilitet beregnes gennem gennemsnittet af de absolutte værdier for afvigelserne i forhold til gennemsnittet.. Betegner den gennemsnitlige afvigelse som D_M, For ikke-grupperede data beregnes middelafvigelsen ved hjælp af følgende formel:

Hvor n er antallet af tilgængelige data, x_jeg repræsenterer hver data og x̄ er gennemsnittet, der bestemmes ved at tilføje alle data og dividere med n:

Den gennemsnitlige afvigelse gør det muligt i gennemsnit at vide, hvor mange enheder dataene afviger fra det aritmetiske gennemsnit og har fordelen ved at have de samme enheder som de data, vi arbejder med.

Eksempel på middelafvigelse

Baseret på dataene fra rækkeviddeeksemplet er antallet af scorede mål:

40, 32, 35, 36, 37, 31, 37, 29, 39

Hvis du vil finde den gennemsnitlige afvigelse D_M Fra disse data er det nødvendigt først at beregne det aritmetiske gennemsnit x̄:

Og nu hvor værdien af ​​x̄ er kendt, fortsætter vi med at finde den gennemsnitlige afvigelse D._M:

= 2,99 ≈ 3 mål

Derfor kan det fastslås, at dataene i gennemsnit er ca. 3 mål væk fra gennemsnittet, hvilket er 35 mål, og som nævnt er det et langt mere præcist mål end området..

Variation

Den gennemsnitlige afvigelse er et meget finere mål for variabilitet end området, men da det beregnes gennem den absolutte værdi af forskellene mellem hver data og middelværdien, giver det ikke større alsidighed set fra et algebraisk synspunkt..

Af denne grund foretrækkes variansen, som svarer til gennemsnittet af den kvadratiske forskel for hver data med gennemsnittet og beregnes ved hjælp af formlen:

I dette udtryk, s^to betegner variansen, og som altid x_jeg repræsenterer hver af dataene, x̄ er middelværdien og n er de samlede data.

Når du arbejder med en prøve i stedet for populationen, foretrækkes det at beregne variansen som denne:

Under alle omstændigheder er variansen karakteriseret ved altid at være en positiv størrelse, men da det er gennemsnittet af de kvadratiske forskelle, er det vigtigt at bemærke, at den ikke har de samme enheder som dataene..

Varianseksempel

For at beregne variansen af ​​dataene i eksemplerne for interval og middelafvigelse fortsætter vi med at erstatte de tilsvarende værdier og udføre den angivne summering. I dette tilfælde vælger vi at dele med n-1:

= 13,86

Standardafvigelse

Variansen har ikke den samme enhed som den variabel, der undersøges, for eksempel, hvis dataene kommer i meter, resulterer variansen i kvadratmeter. Eller i måleksemplet ville det være i mål i kvadrat, hvilket ikke giver mening.

Derfor defineres standardafvigelsen, også kaldet typisk afvigelse, som kvadratroden af ​​variansen:

s = √s^to

På denne måde opnås et mål for variabiliteten af ​​dataene i de samme enheder som disse, og jo lavere værdien af ​​s er, desto mere grupperet er dataene omkring gennemsnittet..

Både variansen og standardafvigelsen er målene for variabilitet, der skal vælges, når det aritmetiske gennemsnit er det mål for den centrale tendens, der bedst beskriver datas opførsel..

Og det er, at standardafvigelsen har en vigtig egenskab, kendt som Chebyshevs sætning: mindst 75% af observationerne er i det interval, der er defineret af x ± 2s. Med andre ord er 75% af dataene højst 2s væk fra gennemsnittet..

På samme måde er mindst 89% af værdierne i en afstand på 3s fra gennemsnittet, en procentdel, der kan udvides, så længe der er mange tilgængelige data, og de følger en normalfordeling..

Figur 2. - Hvis dataene følger en normalfordeling, ligger 95,4 af dem inden for to standardafvigelser på begge sider af gennemsnittet. Kilde: Wikimedia Commons.

Standardafvigelseseksempel

Standardafvigelsen for de data, der er præsenteret i de foregående eksempler, er:

s = √s^to = √13,86 = 3,7 ≈ 4 mål