
Kvantemekanisk model for atomadfærden, eksempler
Det kvantemekanisk model af atomet antager, at dette er dannet af en central kerne, der består af protoner og neutroner. Negativt ladede elektroner omgiver kernen i diffuse områder kendt som orbitaler..
Formen og omfanget af elektroniske orbitaler bestemmes af forskellige størrelser: kernens potentiale og de kvantiserede niveauer af energi og elektronernes vinkelmoment.
Ifølge kvantemekanik har elektroner dobbelt bølgepartikeladfærd, og i atomskala er de diffuse og ikke-punkt. Atomets dimensioner bestemmes praktisk talt af udvidelsen af de elektroniske orbitaler, der omgiver den positive kerne.
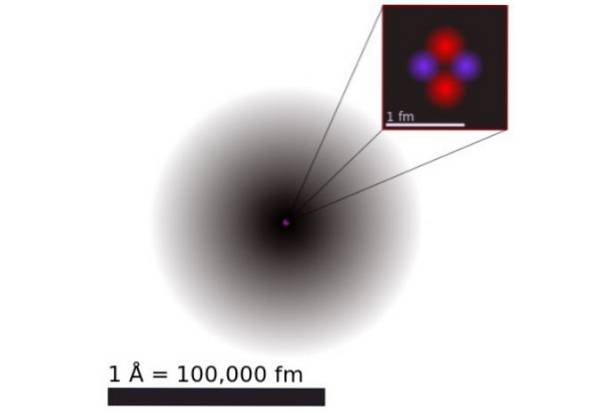
Figur 1 viser strukturen af heliumatomet, som har en kerne med to protoner og to neutroner. Denne kerne er omgivet af sandsynlighedsskyen for de to elektroner, der omgiver kernen, som er hundrede tusind gange mindre. I det følgende billede kan du se heliumatomet med protoner og neutroner i kernen og elektronerne i orbitaler.

Størrelsen på et heliumatom er i størrelsesordenen et angstrøm (1 Å), det vil sige 1 x 10 ^ -10 m. Mens størrelsen på dens kerne er af størrelsesordenen a femtometer (1 fm), det vil sige 1 x 10 ^ -15 m.
På trods af at den er så forholdsvis lille, er 99,9% af atomvægten koncentreret i den lille kerne. Dette skyldes, at protonerne og neutronerne er 2.000 gange tungere end de elektroner, der omgiver dem..
Artikelindeks
- 1 Atomskala og kvanteopførsel
- 1.1 Første kvantemodeller
- 2 Dynamik af materialebølger
- 2.1 Atomiske orbitaler
- 2.2 Kvantumtal
- 3 Orbitalers form og størrelse
- 3.1 Drejningen
- 4 Referencer
Atomskala og kvanteopførsel
Et af de begreber, der havde mest indflydelse på udviklingen af atommodellen, var dualiteten bølge - partikel: opdagelsen af, at ethvert materielt objekt har en materiebølge forbundet med sig.
Formlen til beregning af bølgelængden λ forbundet med et materielt objekt blev foreslået af Louis De Broglie i 1924 og er følgende:
λ = h / (m v)
Hvor h er Plancks konstant, m dejen og v fart.
Ifølge De Broglie's princip har hvert objekt en dobbelt adfærd, men afhængigt af omfanget af interaktionerne, hastigheden og massen kan bølgeopførelsen være mere fremtrædende end partikeladfærden eller omvendt..
Elektronen er lys, dens masse er 9,1 × 10 ^ -31 kg. Den elektroniske hastighed for en elektron er 6000 km / s (halvtreds gange langsommere end lysets hastighed). Denne hastighed svarer til energiværdier i intervallet af snesevis af elektronvolt..
Med ovenstående data og ved hjælp af de Broglie-formlen kan bølgelængden for elektronen opnås:
λ = 6,6 x 10 ^ -34 J s / (9,1 × 10 ^ -31 kg 6 x 10 ^ 6 m / s) = 1 x 10 ^ -10 m = 1 Å
Elektronen ved de typiske energier af atomare niveauer har en bølgelængde af samme størrelsesorden som den for atomskalaen, således at den i denne skala har en bølgeform og ikke en partikel..
Første kvantemodeller
Med tanken om, at elektronen med atomskala har bølgeform, blev de første atommodeller baseret på kvanteprincipper udviklet. Blandt disse skiller sig Bohr-atommodellen ud, som perfekt forudsagde emissionsspektret for brint, men ikke det for andre atomer.
Bohr-modellen og senere Sommerfeld-modellen var semi-klassiske modeller. Det vil sige, at elektronen blev behandlet som en partikel udsat for den elektrostatiske tiltrækningskraft af kernen, der kredsede omkring den, styret af Newtons anden lov..
Ud over klassiske baner tog disse første modeller hensyn til, at elektronen havde en tilknyttet materialebølge. Kun baner, hvis omkreds var et helt antal bølgelængder, var tilladt, da de, der ikke opfylder dette kriterium, forsvinder af destruktiv interferens..
Det er så, at kvantiseringen af energi vises for første gang i atomstrukturen..
Ordet kvante Det kommer netop af det faktum, at elektronen kun kan påtage sig nogle diskrete energiværdier i atomet. Dette falder sammen med Plancks fund, som bestod i opdagelsen af, at en frekvensstråling F interagerer med stof i energipakker E = h f, hvor h er Plancks konstant.
Dynamik af materialebølger
Der var ikke længere nogen tvivl om, at elektronen på atomniveau opførte sig som en materialebølge. Det næste trin var at finde ligningen, der styrer deres adfærd. Denne ligning er hverken mere eller mindre end Schrodinger-ligningen, der blev foreslået i 1925.
Denne ligning relaterer til og bestemmer bølgefunktionen ψ forbundet med en partikel, såsom elektronen, med dets interaktionspotentiale og dets samlede energi OG. Dets matematiske udtryk er:


Lighed i Schrodinger-ligningen gælder kun for nogle værdier af den samlede energi OG, hvilket giver anledning til kvantisering af energi. Bølgefunktionen af elektroner, der udsættes for kernens potentiale, opnås fra opløsningen af Schrodinger-ligningen.
Atomiske orbitaler
Den absolutte værdi af bølgefunktionen i kvadrat |ψ| ^ 2, giver sandsynlighedsamplituden for at finde elektronen i en given position.
Dette fører til begrebet orbital, som er defineret som det diffuse område optaget af elektronen med ikke-nul sandsynlighedsamplitude for de diskrete værdier af energi og vinkelmoment bestemt af opløsningerne i Schrodinger-ligningen.
Kendskabet til orbitalerne er meget vigtigt, fordi det beskriver atomstrukturen, den kemiske reaktivitet og de mulige bindinger til dannelse af molekyler.
Brintatomet er det enkleste af alle, fordi det har en ensom elektron, og det er den eneste, der tillader en nøjagtig analytisk løsning af Schrodinger-ligningen.
Dette enkle atom har en kerne, der består af en proton, der producerer et centralt potentiale for Coulomb-tiltrækning, der kun afhænger af radius. r, så det er et system med sfærisk symmetri.
Bølgefunktionen afhænger af positionen givet af de sfæriske koordinater i forhold til kernen, da det elektriske potentiale har central symmetri.
Desuden kan bølgefunktionen skrives som et produkt af en funktion, der kun afhænger af den radiale koordinat, og en anden, der afhænger af vinkelkoordinaterne:

Kvantumtal
Løsningen af den radiale ligning producerer de diskrete energiværdier, der afhænger af et heltal n, kaldte hovedkvantumnummer, som kan tage positive heltalværdier 1, 2, 3, ...
Diskrete energiværdier er negative værdier givet ved følgende formel:

Vinkelligningsløsningen definerer de kvantiserede værdier af vinkelmomentet og dets z-komponent, hvilket giver anledning til kvantetallene l Y ml.
Kvantetallet for vinkelmoment l går fra 0 til n-1. Kvantumnummer ml kaldes det magnetiske kvantetal og går fra -l så længe +l. For eksempel ja l var 2, ville det magnetiske kvantetal tage værdierne -2, -1, 0, 1, 2.
Orbitalernes form og størrelse
Orbitalens radiale rækkevidde bestemmes af radi bølgefunktiontil. Det er større, når elektronens energi stiger, det vil sige, når det vigtigste kvantetal stiger.
Den radiale afstand måles normalt i Bohr-radier, som for den laveste energi af brint er 5,3 X 10-11 m = 0,53 Å.

Men orbitalernes form bestemmes af værdien af det kantede kvantetal. Hvis l = 0 har vi en sfærisk orbital kaldet s, hvis l = 1 har vi en lobuleret orbital kaldet s, som kan have tre retninger i henhold til det magnetiske kvantetal. Den følgende figur viser formen på orbitalerne.
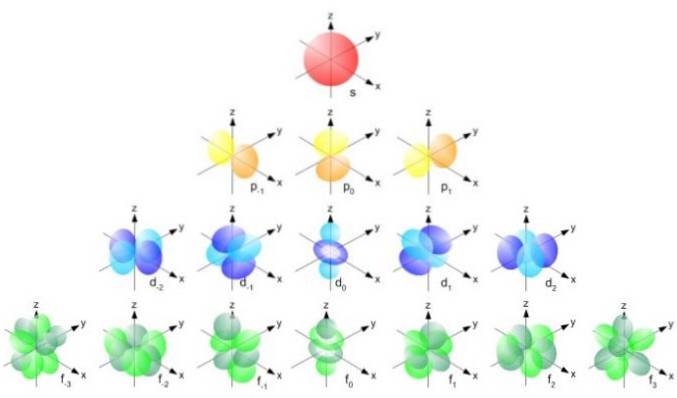
Disse orbitaler pakker ind i hinanden i henhold til elektronernes energi. For eksempel viser følgende figur orbitalerne i et natriumatom.
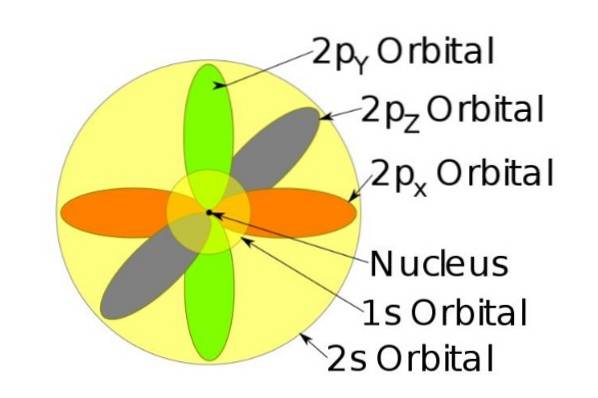
Drejningen
Den kvantemekaniske model af Schrödinger-ligningen inkorporerer ikke elektronens spin. Men det tages i betragtning gennem Pauli-udelukkelsesprincippet, som indikerer, at orbitaler kan befolkes med op til to elektroner med spin-kvantetal s = + ½ og s = -½.
For eksempel har natriumionen 10 elektroner, det vil sige, hvis vi henviser til den foregående figur, er der to elektroner til hver orbital.
Men hvis det er det neutrale natriumatom, er der 11 elektroner, hvoraf den sidste vil indtage en 3s orbital (ikke vist i figuren og med en større radius end 2s). Atommets spin er afgørende i et stofs magnetiske egenskaber.
Referencer
- Alonso - Finn. Kvante- og statistiske fundamenter. Addison Wesley.
- Eisberg - Resnick. Kvantefysik. Limusa - Wiley.
- Gasiorowicz. Kvantefysik. John Wiley & Sons.
- HSC. Fysik kursus 2. Jacaranda plus.
- Wikipedia. Schrodingers atommodel. Gendannet fra: Wikipedia.com



Endnu ingen kommentarer