
Pendulbevægelse
Hvad er pendulbevægelsen?
Det pendulbevægelse Det er en frem og tilbage bevægelse lavet af en mere eller mindre tung genstand, kaldet et pendul, ophængt af et reb eller en lysstang, fastgjort i den anden ende.
Pendulet får en indledende impuls og får lov til at svinge, på denne måde beskriver objektet buer frem og tilbage. Dette er princippet om, hvordan pendulure, gynger, gyngestole og metronomer pendul, bruges til at markere tidspunkterne i musik.
Det siges, at omkring 1581 observerede Galileo Galilei svingningen af en lampe i katedralen i Pisa og observerede, at selv om amplituden af lysestageens svingning var faldende på grund af friktion med luften, ikke varigheden af lampens cyklus..
Dette fangede Galileos opmærksomhed, der besluttede at fortsætte med undersøgelsen og fastslog, at pendulets periode ikke afhænger af massen, men af kvadratroden af akkordens længde, som det vil fremgå senere..
Pendulets bevægelsesegenskaber
Et pendul er meget let at bygge, da det er nok med en lodlinie, der hænger fra en bomuldstråd og holdes fast i den anden ende med fingrene eller ved at fastgøre den til en støtte som et søm..
Efter den lille indledende impuls er vægten ansvarlig for at holde pendulet oscillerende, selvom friktionen mindsker bevægelsens amplitude, indtil den endelig ophører fuldstændigt..
Hovedkarakteristikken ved pendulbevægelsen er at være gentagne, da det er en frem og tilbage bevægelse. For at lette studiet er det nu praktisk at foretage nogle forenklinger for at fokusere på en enklere model, kaldet simpelt pendul.
Det enkle pendul

Det er et ideelt system, der består af en lodlinie, betragtes som en punktmasse m, fastgjort til et let, uudvideligt reb med længde L. Karakteristika ved dette system er:
- Har en gentagen og periodisk bevægelse, der består af at gå frem og tilbage en bue med en radius på lig med L.
- Tager ikke friktion i betragtning.
- Bevægelsesområdet er lille (< 5º).
- Perioden er uafhængig af massen m, og afhænger udelukkende af længden L pendul.
Formler og ligninger
Følgende er et diagram over det enkle pendul, hvorpå to kræfter virker: vægten P af størrelsesordenen mg, som er rettet lodret nedad og spændingen T På rebet. Friktion tages ikke i betragtning.
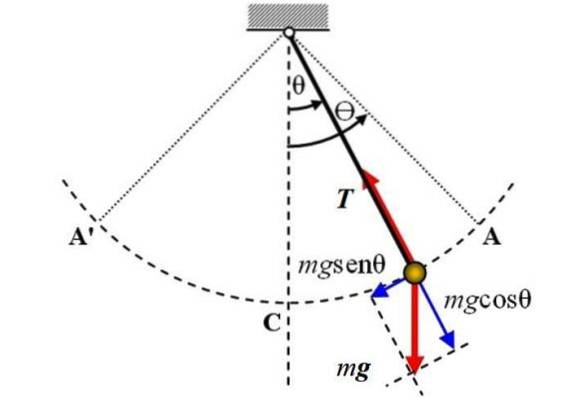
Referenceaksen er den lodrette akse og falder sammen med positionen θ = 0, derfra måles vinkelforskydningen θ enten i en eller anden retning. + Tegnet kan tildeles det højre skift i figuren.
For at studere bevægelsen af pendulet vælges et koordinatsystem med oprindelsen ved selve pendulet. Dette system har en tangentiel koordinat til omkredsbuen A'CA beskrevet af pendulet såvel som en radial koordinat, rettet mod centrum af banen..
I det øjeblik, der vises i figuren, bevæger pendulet sig til højre, men den tangentielle tyngdekomponent, kaldet Ft, er ansvarlig for at få ham tilbage. Det kan ses af figuren, at denne komponent har den modsatte retning af bevægelse.
Med hensyn til spændingen i rebet er det afbalanceret med komponenten i vægten mgcosθ.

Vinkelforskydning
Vi skal udtrykke ligningen i form af en enkelt variabel og huske, at vinkelforskydningen θ og den tilbagelagte bue er relateret til ligningen:
s = L.θ
Massen annulleres på begge sider, og hvis amplituden er lille, er vinklen θ også, så følgende tilnærmelse er gyldig:
sen θ ≈ θ
Med dette opnås følgende differentialligning for variablen θ (t):


Denne ligning er meget let at løse, da løsningen er en funktion, hvis andet derivat er selve funktionen. Der er tre alternativer: en cosinus, en sinus eller en eksponentiel. Cosinus-funktionen er valgt til vinkelforskydning θ (t), da den er en velkendt og let at håndtere funktion.
Læseren kan kontrollere, ved at differentiere to gange, at følgende funktion opfylder differentialligningen:
θ (t) = θm cos (ωt + φ)
Hvor θm er den maksimale vinkel, som pendulet bevæger sig i forhold til lodret, og vinkelfrekvensen ω er:

Periodens ligning
Perioden T for bevægelsen er den tid det tager at udføre en cyklus og defineres som:

Erstatter ω:

Som nævnt ovenfor afhænger perioden ikke af pendulets masse, men kun af længden..
Eksempler på pendulbevægelse
Pulsmåling
Galileo havde ideen om at måle hjerterytmen hos mennesker, justere længden af pendulet for at få perioden til at falde sammen med slagene i en persons hjerte.
Penduluret
Dette er utvivlsomt et af de mest kendte eksempler på pendulbevægelse. Pendulurfremstilling handler lige så meget om videnskab, som det handler om kunst. Den hollandske fysiker Christian Huygens (1629-1695) udviklede det første pendulur i 1656, baseret på den undersøgelse, der blev foretaget for flere år siden af Galileo.
Foucaults pendul

Det er et noget andet pendul end det ovenfor beskrevne, da det er i stand til at rotere i ethvert lodret plan. Det blev skabt af den franske fysiker Léon Foucault (1819-1868) og bruges til at visualisere jordens rotation.
Træning løst
Et simpelt pendul passerer hver 0,5 sek gennem ligevægtspositionen. Hvad er trådens længde?
Opløsning
Da perioden er den tid, det tager at gennemføre en komplet cyklus, hvor den passerer gennem ligevægtspositionen to gange: den ene går og den anden tilbage, så:
T = 2 × 0,5 s = 1 s
Fra:

Trådens længde L er ryddet:

Tråden er 0,25 m eller 25 cm lang.
Referencer
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 2. dynamik. Redigeret af Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Katz, D. 2013. Fysik for forskere og ingeniører. Fundamenter og forbindelser. Cengage læring.
- Knight, R. 2017. Fysik for forskere og teknik: en strategi tilgang. Pearson.


Endnu ingen kommentarer