
Retlinjære bevægelsesegenskaber, typer og eksempler
Det retilineal bevægelse er den, hvor mobilen bevæger sig langs en lige linje og derfor kører i en dimension, derfor kaldes den også endimensionel bevægelse. Denne lige linje er bane eller sti efterfulgt af det bevægelige objekt. Biler, der bevæger sig langs avenuen i figur 1, følger denne type bevægelse.
Det er den enkleste bevægelsesmodel, du kan forestille dig. De daglige bevægelser af mennesker, dyr og ting kombinerer normalt bevægelser i en lige linje med bevægelser langs kurver, men nogle, der udelukkende er retlinede, observeres ofte.

Her er nogle gode eksempler:
- Når du løber langs et 200 meter lige spor.
- At køre bil på lige vej.
- At droppe et objekt frit fra en bestemt højde.
- Når en bold kastes lodret opad.

Nu opnås målet med at beskrive en bevægelse ved at specificere egenskaber som:
- Position
- Forskydning
- Hastighed
- Acceleration
- Vejr.
For at en observatør kan opdage en genstands bevægelse, skal de have et referencepunkt (oprindelsen O) og have etableret en bestemt retning, i hvilken den kan bevæge sig, hvilket kan være aksen x, aksen Y eller andre.
Hvad angår objektet, der bevæger sig, kan det have et uendeligt antal former. Der er ingen begrænsninger i denne henseende, men i alt det følgende antages det, at mobilen er en partikel; et objekt så lille, at dets dimensioner ikke er relevante.
Dette vides ikke at være tilfældet for makroskopiske objekter; det er dog en model med gode resultater til beskrivelse af et objekts globale bevægelse. På denne måde kan en partikel være en bil, en planet, en person eller enhver anden genstand, der bevæger sig.
Vi vil begynde vores undersøgelse af retlinet kinematik med en generel tilgang til bevægelse, og derefter vil særlige tilfælde som dem, der allerede er nævnt, blive undersøgt..
Artikelindeks
- 1 Generelle egenskaber ved retlinet bevægelse
- 1.1 Position
- 1.2 Forskydning
- 1.3 Afstand tilbagelagt
- 1.4 Gennemsnitlig hastighed
- 1.5 Øjeblikkelig hastighed
- 1.6 Hastighed
- 1.7 Gennemsnitlig acceleration og øjeblikkelig acceleration
- 2 slags
- 2.1 Bevægelse med konstant acceleration
- 2.2 Vandrette bevægelser og lodrette bevægelser
- 3 Arbejdede eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referencer
Generelle egenskaber ved retlinet bevægelse
Den følgende beskrivelse er generel og gælder for enhver form for en-dimensionel bevægelse. Den første ting er at vælge et referencesystem. Linjen langs hvilken bevægelsen finder sted vil være aksen x. Bevægelsesparametre:
Position

Det er vektoren, der går fra oprindelsen til det punkt, hvor objektet er på et givet øjeblik. I figur 2 viser vektoren x1 angiver placeringen af mobilen, når den er i koordinaten P1 og han med tiden t1. Enhederne i positionsvektoren i det internationale system er meter.
Forskydning
Forskydningen er den vektor, der angiver ændringen i position. I figur 3 er bilen flyttet fra position P1 at placere Pto, derfor er dens forskydning Δx = xto - x1. Forskydningen er subtraktion af to vektorer, den symboliseres med det græske bogstav Δ (“delta”), og det er igen en vektor. Dens enheder i det internationale system er meter.
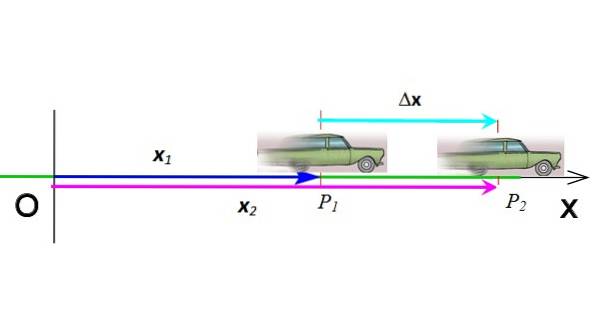
Vektorer er angivet med fed skrift i trykt tekst. Men at være på samme dimension, hvis du vil, kan du undvære vektornotationen.
Afstand tilbagelagt
Afstand d rejst af det bevægelige objekt er den absolutte værdi af forskydningsvektoren:
d = ΙΔxΙ = Δx
At være en absolut værdi, er den tilbagelagte afstand altid større end eller lig med 0, og dens enheder er de samme som position og forskydning. Absolut værdi notation kan udføres med modulo bjælker eller blot ved at fjerne den fed skrift i udskrevet tekst.
Gennemsnitshastighed
Hvor hurtigt ændres positionen? Der er langsomme og hurtige mobiltelefoner. Nøglen har altid været hastighed. For at analysere denne faktor analyseres positionen x funktion af tiden t.
Gennemsnitshastighed vm (se figur 4) er hældningen af sekantlinjen (fuchsia) til kurven x vs. t og giver global information om mobilens bevægelse i det betragtede tidsinterval.
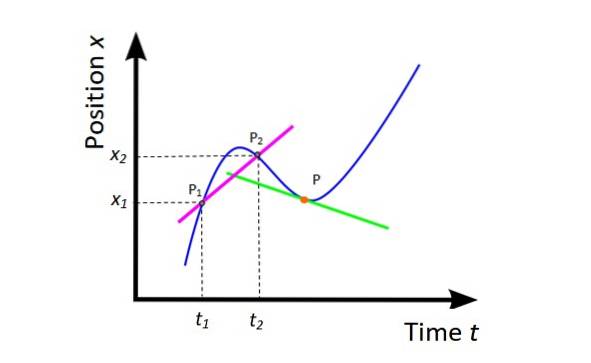
vm = (xto - x1) / (tto -t1) = Δx / Δt
Gennemsnitshastighed er en vektor, hvis enheder i det internationale system er meter / sekund (Frk).
Øjeblikkelig hastighed
Gennemsnitlig hastighed beregnes ved at tage et målbart tidsinterval, men rapporterer ikke, hvad der sker inden for dette interval. For at kende hastigheden til enhver tid skal du gøre tidsintervallet meget lille, matematisk svarer det til at gøre:
Δt → 0
Ligningen ovenfor er angivet for gennemsnitshastigheden. På denne måde opnås den øjeblikkelige hastighed eller simpelthen hastighed:
Geometrisk er den afledte af positionen i forhold til tiden hældningen af linjen, der tangerer til kurven x vs. t på et givet tidspunkt. I figur 4 er punktet orange og tangentlinjen grøn. Den øjeblikkelige hastighed på det tidspunkt er hældningen på den linje.
Fart
Hastighed defineres som den absolutte værdi eller hastighedsmodul og er altid positiv (skilte, veje og motorveje er altid positive, aldrig negative). Udtrykkene "hastighed" og "hastighed" kan bruges om hverandre på daglig basis, men i fysik er forskellen mellem vektor og skalar nødvendig.
v = ΙvΙ = v
Gennemsnitlig acceleration og øjeblikkelig acceleration
Hastigheden kan ændre sig i løbet af bevægelsen, og virkeligheden er, at det forventes at gøre det. Der er en størrelse, der kvantificerer denne ændring: acceleration. Hvis vi bemærker, at hastighed er ændringen i position med hensyn til tid, er acceleration ændringen i hastighed i forhold til tid.
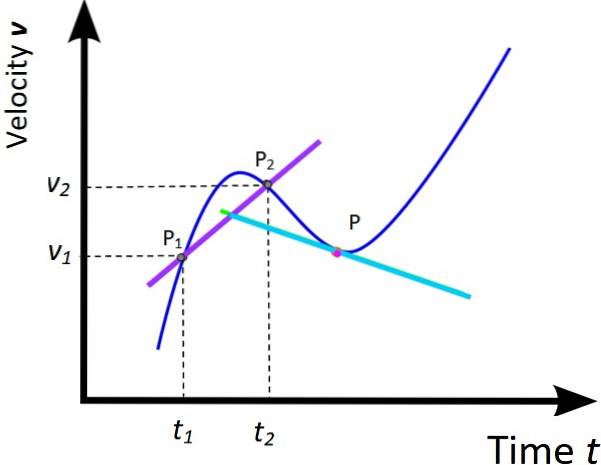
Behandlingen til grafen for x vs. t af de to foregående sektioner kan udvides til den tilsvarende graf for v vs. t. Derfor er en gennemsnitlig acceleration og en øjeblikkelig acceleration defineret som:
tilm = (vto - v1) / (tto -t1) = Δv / Δt (Hældning af den lilla linje)
I en-dimensionel bevægelse har vektorer efter konvention positive eller negative tegn afhængigt af om de går den ene eller den anden vej. Når acceleration har samme retning som hastighed, øges dens størrelse, men når den har den modsatte retning, og hastigheden mindsker dens størrelse. Det siges derefter, at bevægelsen er forsinket.
Typer
Klassificeringen af retlinede bevægelser er generelt baseret på:
- Uanset om accelerationen er konstant eller ej.
- Bevægelse løber langs en vandret eller lodret linje.
Bevægelse med konstant acceleration
Når accelerationen er konstant, er den gennemsnitlige acceleration tilm svarer til øjeblikkelig acceleration til og der er to muligheder:
- At accelerationen er lig med 0, i hvilket tilfælde hastigheden er konstant, og der er en ensartet retlinet bevægelse eller MRU.
- Konstant acceleration bortset fra 0, hvor hastigheden stiger eller falder lineært med tiden (den ensartet varierede, retlinede bevægelse eller MRUV):
Hvor vF Y tF er henholdsvis sluthastighed og tid og veller Y teller de er starthastighed og tid. Ja teller = 0, Løsning for den endelige hastighed har vi den allerede kendte ligning for den endelige hastighed:
vF = veller + på
Følgende ligninger er også gyldige for denne bevægelse:
- Position som en funktion af tiden: x = xeller + veller .t + ½ vedto
- Hastighed som funktion af position: vFto = vellerto + 2..Δx (Med Δx = x - xeller)
Vandrette bevægelser og lodrette bevægelser
Horisontale bevægelser er dem, der finder sted langs den vandrette akse eller x-aksen, mens lodrette bevægelser gør det langs y-aksen. Vertikale bevægelser under tyngdekraften er de mest hyppige og interessante.
I de tidligere ligninger tager vi a = g = 9,8 m / sto rettet lodret nedad, en retning, der næsten altid vælges med et negativt tegn.
På denne måde, vF = veller + på Det transformerer ind vF = veller - gt og hvis starthastigheden er 0, fordi objektet blev droppet frit, forenkles det yderligere til vF = - gt. Så længe der ikke tages højde for luftmodstand, naturligvis.
Arbejdede eksempler
Eksempel 1
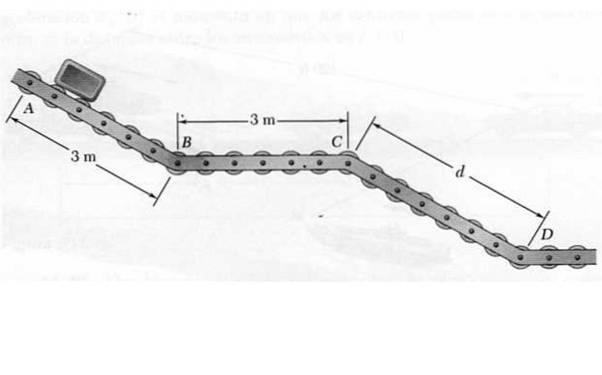
På punkt A frigøres en lille pakke, der bevæger sig langs transportbåndet med glideskiver ABCD vist i figuren. Under nedstigning på skråningerne AB og CD har pakken en konstant acceleration på 4,8 m / sto, mens i det vandrette afsnit BC opretholder konstant hastighed.

Ved at vide, at hastigheden, hvormed pakken ankommer til D, er 7,2 m / s, skal du bestemme:
a) Afstanden mellem C og D..
b) Den tid, det tager for pakken at nå slutningen.
Opløsning
Pakkens bevægelse udføres i de viste tre retlinede sektioner, og for at beregne det, der kræves, kræves hastigheden i punkterne B, C og D. Lad os analysere hvert afsnit separat:
Sektion AB
Da tiden ikke er tilgængelig i dette afsnit, vil den blive brugt vFto = vellerto + 2..Δx med vo = 0:
vFto = 2a.Δx → vFto= 2,8 m / sto . 3 m = 28,8 mto/ sto → vF = 5,37 m / s = vB
Den tid det tager pakken at rejse gennem sektionen AB er:
tAB = (vF - veller) / a = 5,37 m / s / 4,8 m / sto = 1,19 s
Afsnit f.Kr.
Hastigheden i sektion BC er derfor konstant vB = vC = 5,37 m / s. Den tid det tager for pakken at rejse dette afsnit er:
tF.Kr. = afstand F.Kr. / vB = 3 m / 5,37 m / s = 0,56 s
Afsnit CD
Den indledende hastighed for dette afsnit er vC = 5,37 m / s, den endelige hastighed er vD = 7,2 m / s, ved vDto = vCto + 2. a. d værdien af er ryddet d:
d = (vDto - vCto) /2.a = (7.2to - 5.37to)/to x 4,8 m = 2,4 m
Tid beregnes som:
tCD = (vD - vC) / a = (7,2 - 5,37) / 4,8 s = 0,38 s.
Svarene på de stillede spørgsmål er:
a) d = 2,4 m
b) Rejsetiden er tAB + tF.Kr. + tCD = 1,19 s +0,56 s +0,38 s = 2,13 s.
Eksempel 2
En person er under en vandret port, der oprindeligt er åben og 12 m høj. Personen kaster lodret en genstand mod porten med en hastighed på 15 m / s.
Porten vides at lukke 1,5 sekunder efter at personen har kastet genstanden fra en højde på 2 meter. Luftmodstand tages ikke i betragtning. Besvar følgende spørgsmål og begrundelse:
a) Kan genstanden passere gennem porten, før den lukker?
b) Vil objektet nogensinde kollidere med den lukkede port? Hvis ja, hvornår gør det?
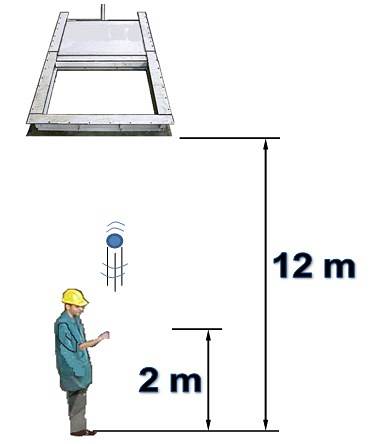
Svar til)
Der er 10 meter mellem boldens startposition og porten. Det er et lodret opadkast, hvor denne retning betragtes som positiv.
Du kan finde ud af den hastighed, det tager at nå denne højde, med dette resultat beregnes den tid, det tager at gøre det, og sammenlignes med portens lukketid, som er 1,5 sekunder:
vF to= veller to- 2 g. Δog → vF = (15to - to x 9.8 x10)1/2 m = 5,39 m / s
t = (vF - veller) / g = (5,39 - 15) / (-9,8) s = 0,98 s
Da denne tid er mindre end 1,5 sekunder, konkluderes det, at objektet kan passere gennem porten mindst en gang.
Svar b)
Vi ved allerede, at objektet formår at passere gennem porten, mens det går op, lad os se om det giver det en chance for at passere igen, når det går ned. Hastigheden, når den når portens højde, har samme størrelse som når den går op ad bakke, men i den modsatte retning. Derfor arbejder vi med -5,39 m / s, og den tid det tager at nå denne situation er:
t = (vF - veller) / g = (-5,39 - 15) / (-9,8) s = 2,08 s
Da porten forbliver åben i kun 1,5 s, er det tydeligt, at den ikke har tid til at passere igen, før den lukker, da den finder den lukket. Svaret er: objektet, hvis det kolliderer med den lukkede luge efter 2,08 sekunder efter at være kastet, når den allerede er faldende.
Referencer
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 1. kinematik. Redigeret af Douglas Figueroa (USB) .69-116.
- Giancoli, D. Fysik. (2006). Principper med applikationer. 6th Udgave. Prentice Hall. 22-25.
- Kirkpatrick, L. 2007. Fysik: Et blik på verden. 6ta Forkortet udgave. Cengage læring. 23 - 27.
- Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 21-22.
- Rex, A. (2011). Grundlæggende om fysik. Pearson. 33 - 36
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14th. Red. Bind 1. 50 - 53.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7mor. Udgave. Mexico. Cengage Learning Editors. 23-25.
- Serway, R., Vulle, C. (2011). Grundlæggende om fysik. 9na Ed. Cengage Learning. 43 - 55.
- Wilson, J. (2011). Fysik 10. Pearson Education. 133 - 149.


Endnu ingen kommentarer