Relativ bevægelse i en dimension, i to dimensioner, øvelser

Det relativ bevægelse af en partikel eller en genstand er den, der observeres med hensyn til et bestemt referencepunkt, som observatøren har valgt, som kan være fast eller i bevægelse. Hastighed refererer altid til et eller andet koordinatsystem, der bruges til at beskrive det.

For eksempel er passagererne i en bil i bevægelse og som sover komfortabelt i sit sæde i ro i forhold til føreren, men ikke for en observatør, der står på fortovet, og som ser bilen gå forbi..

Derefter er bevægelsen altid relativ, men det sker, at koordinat- eller referencesystemet generelt vælges med sin oprindelse i Jorden eller jorden, et sted, der betragtes som stille. På denne måde er bekymringen fokuseret på at beskrive bevægelsen af ​​det objekt, der undersøges..

Er det muligt at beskrive den sovende copilots hastighed sammenlignet med en passager, der rejser i en anden bil? Svaret er ja. Der er frihed til at vælge værdien af ​​(x_eller, Y_eller, z_eller): oprindelsen af ​​referencesystemet. Valget er vilkårligt og afhænger af observatørens præference samt den lethed, det giver for at løse problemet..

Artikelindeks

• 1 Relativ bevægelse i en dimension
  • 1.1 - Arbejdet eksempel 1
• 2 Relativ bevægelse i to og tre dimensioner
  • 2.1 -Løst øvelse 2 
  • 2.2 -Løst øvelse 3
• 3 Referencer

Relativ bevægelse i en dimension

Når bevægelsen finder sted langs en lige linje, har mobiltelefoner hastigheder i samme retning eller i den modsatte retning, begge set af en observatør, der står på Jorden (T). Bevæger observatøren sig i forhold til mobiltelefoner? Ja, med den samme hastighed, som de har, men i den modsatte retning.

Hvordan bevæger den ene mobil sig i forhold til den anden? For at finde ud af tilføjes hastighederne vektorielt.

-Arbejdet eksempel 1

Henvis til den viste figur, angiv den relative hastighed for bil 1 i forhold til bil 2 i hver situation.

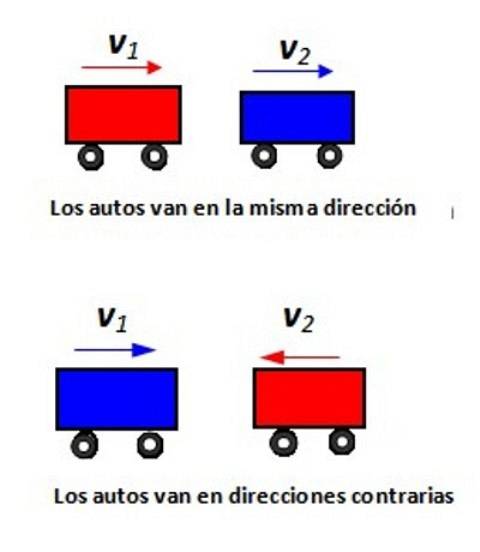
Opløsning

Vi tildeler et positivt tegn til hastighederne til højre og et negativt tegn til venstre. Hvis en mobil går til højre i 80 km / t, ser en passager på denne mobil observatøren på Jorden bevæge sig i - 80 km / t.

Antag at alt sker langs x-aksen. I den følgende figur bevæger den røde bil sig i +100 km / t (set fra T) og er ved at passere den blå bil, der kører i +80 km / t (set også fra T). Hvor hurtigt nærmer en passager i den blå bil sig til den røde bil?

Mærkaterne er: v _1/2 hastighed på bil 1 i forhold til bil 2, v_{1 / T.} bilens hastighed i forhold til T, v_{T / 2} hastighed af T i forhold til 2. Vektortilsætning:

v_1/2 = v_{1 / T.} + v_{T / 2} = (+100 km / t - 80 km / t) x= 20 km / t x

Vi kan undvære vektornotationen. Bemærk abonnementerne: Ved at multiplicere de to til højre skal du få den til venstre.

Og når de går den anden vej? Nu v_{1 / T.} = + 80 km / t og v_{2 / T.} = -100 km / t, derfor v_{T / 2} = + 100 km / t. Passagererne i den blå bil vil se den røde bil nærme sig:

v_{1/2 =} v_{1 / T.} + v_{T / 2} = +80 km / t +100 km / t = 180 km / t

Relativ bevægelse i to og tre dimensioner

I følgende skema, r er flyets position set fra systemet X og Z, r'er positionen fra systemet X og Z ' Y R er systemets position med en præmie i forhold til systemet uden præmie. De tre vektorer danner en trekant, hvori R + r'= r, Dermed r'= r - R.

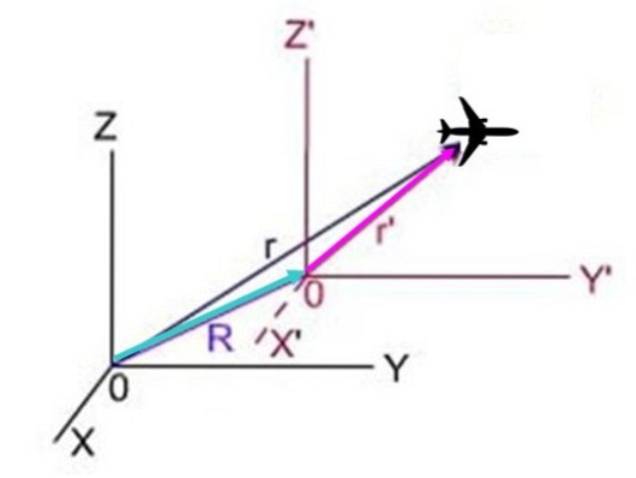
Da afledningen med hensyn til positionstid er nøjagtigt hastigheden, resulterer det:

v'= v - eller

I denne ligning v'er flyets hastighed i forhold til systemet X og Z ', v er hastigheden i forhold til systemet X og Z Y eller er det primære systems konstante hastighed i forhold til det ikke-primede system.

-Træning løst 2 

Et fly er på vej mod nord med en hastighed på 240 km / t. Pludselig begynder vinden at blæse fra vest til øst med en hastighed på 120 km / afhængigt af jorden.

Find: a) Flyets hastighed i forhold til jorden, b) Pilotens afvigelse c) Den korrektion, som piloten skal foretage for at kunne sigte direkte mod nord og den nye hastighed i forhold til jorden, en gang korrektionen er foretaget.

Opløsning

a) Der er følgende elementer: plan (A), jord (T) og vind (V).

I koordinatsystemet, hvor nord er + y-retningen og vest-øst-retningen er + x, har vi de givne hastigheder og deres respektive etiket (abonnementer):

v _AV = 240 km / t (+Y); v _{V / T} = 120 km / t (+x); v _{A / T} = ?

Den rigtige vektorsum er:

v _{A / T} = v _AV + v _{V / T} = 240 km / t (+Y) + 120 km / t (+x)

Størrelsen af ​​denne vektor er: v _{A / T} = (240 ^to+ 120^to)^1/2 km / t = 268,3 km / t

b) θ = arctg (v _AV / v _{V / T}) = arctg (240/120) = 63,4 º Nord for Øst eller 26,6 º Nordøst.

c) For at fortsætte nordpå med denne vind bliver du nødt til at pege flyets bue mod nordvest, så vinden skubber dig direkte mod nord. I dette tilfælde vil flyets hastighed set fra jorden være i + y retning, mens flyets hastighed i forhold til vinden vil være nordvest (det behøver ikke nødvendigvis at være 26,6º).

Af Pythagoras sætning:

v _{A / T} = (240 ^to- 120^to)^1/2 km / t = 207,8 km / t

α = arctg (v _{V / T} / v _{A / T} ) = arctg (120 / 207.8) = 30º nordvest

-Træning løst 3

Det tager en person 2 minutter at gå ned ad en stationær rulletrappe. Hvis stigen fungerer, tager det personen 1 minut at gå ned, mens den står stille. Hvor lang tid tager det for personen at gå ned med stigen i gang?

Opløsning

Der er tre elementer at overveje: personen (P), stigen (E) og jorden (S), hvis relative hastigheder er:

v_{P / E} : personens hastighed i forhold til stigen v_{DET ER}: stigenes hastighed i forhold til jorden; v_{P / S}: personens hastighed i forhold til jorden.

Som set fra jorden af ​​en fast observatør, har den person, der stiger ned ad stigen (E), en hastighed v _{P / S} givet af:

v _{P / S} = v_{P / E} + v_{DET ER}

Den positive retning går ned ad stigen. Være t  den tid det tager at gå ned og L afstand. Størrelsen af ​​personens hastighed v _{P / S} det er:

v_{P / S} = L / t

t₁ er det tid det tager at gå ned med stigen stoppet: v _{P / E} = L / t₁

Og T_to den der stadig bringer dig ned på den bevægelige trappe: v _{DET ER} = L / t_to

Kombination af udtryk:

L / t = L / t₁ + L / t_to

Udskiftning af numeriske værdier og løsning t:

1 / t = 1 / t₁ + 1 / t_to = 1/2 + 1/1 = 1,5

Så t = 1 / 1,5 minutter = 40 sekunder.

Referencer

1. Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physics Series for Sciences and Engineering. Bind 3. Udgave. Kinematik. 199-232.
3. Giancoli, D. 2006. Fysik: Principper med applikationer. 6^th. Ed. Prentice Hall. 62-64.
4. Relativ bevægelse. Gendannet fra: courses.lumenlearning.com
5. Wilson, J. 2011. Fysik 10. Pearson Education. 166-168.